\(\left|\dfrac{4}{3}x-\dfrac{1}{4}\right|>=0\forall x\)

=>\(A=\left|\dfrac{4}{3}x-\dfrac{1}{4}\right|-\dfrac{2}{11}>=-\dfrac{2}{11}\forall x\)

Dấu '=' xảy ra khi \(\dfrac{4}{3}x-\dfrac{1}{4}=0\)

=>\(\dfrac{4}{3}x=\dfrac{1}{4}\)

=>\(x=\dfrac{1}{4}:\dfrac{4}{3}=\dfrac{3}{16}\)

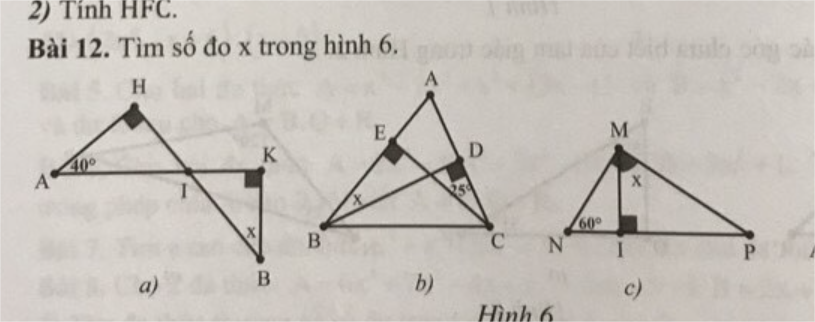
a: Ta có: \(\widehat{HIA}+\widehat{HAI}=90^0\)(ΔHAI vuông tại H)

\(\widehat{KIB}+\widehat{KBI}=90^0\)(ΔKIB vuông tại K)

mà \(\widehat{HIA}=\widehat{KIB}\)(hai góc đối đỉnh)

nên \(\widehat{HAI}=\widehat{KBI}\)

=>\(x=40^0\)

b: Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)

nên BEDC là tứ giác nội tiếp

=>\(x=\widehat{EBD}=\widehat{ECD}=35^0\)

c: Ta có: \(\widehat{IMP}+\widehat{IPM}=90^0\)(ΔMIP vuông tại I)

\(\widehat{MPN}+\widehat{MNP}=90^0\)(ΔMNP vuông tại M)

Do đó: \(x=\widehat{IMP}=\widehat{N}=60^0\)

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)

=>\(2\left(\widehat{IBC}+\widehat{ICB}\right)+50^0=180^0\)

=>\(\widehat{IBC}+\widehat{ICB}=\dfrac{180^0-50^0}{2}=65^0\)

Xét ΔIBC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)

=>\(\widehat{BIC}+65^0=180^0\)

=>\(\widehat{BIC}=180^0-65^0=115^0\)

đề làm sao ấy bn nhỉ ?

Ta có: \(\widehat{BDA}+\widehat{DBA}=90^0\)(ΔBAD vuông tại A)

\(\widehat{CEB}+\widehat{CBE}=90^0\)(ΔCBE vuông tại C)

mà \(\widehat{DBA}=\widehat{CBE}\)

nên \(\widehat{BDA}=\widehat{CEB}\)

=>\(\widehat{CED}=\widehat{CDE}\)

=>ΔCDE cân tại C

ΔCDE cân tại C

mà CH là đường cao

nên CH là phân giác của góc ECD

\(\dfrac{27^4\cdot4^3}{9^5\cdot8^2}=\dfrac{\left(3^3\right)^4\cdot2^6}{\left(3^2\right)^5\cdot2^6}=\dfrac{3^{12}}{3^{10}}=3^2=9\)

Đặt \(B=\dfrac{5}{1\cdot2\cdot3}+\dfrac{5}{2\cdot3\cdot4}+...+\dfrac{5}{98\cdot99\cdot100}\)

=>\(B=5\left(\dfrac{1}{1\cdot2\cdot3}+\dfrac{1}{2\cdot3\cdot4}+...+\dfrac{1}{98\cdot99\cdot100}\right)\)

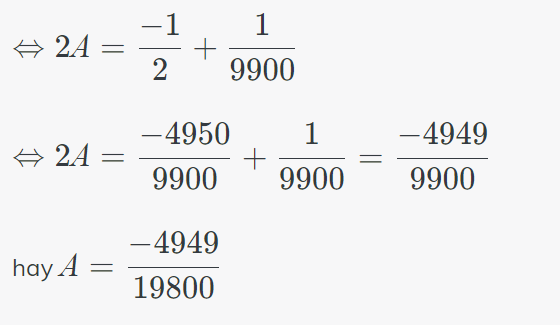
\(B=5A=\dfrac{-5\cdot4949}{19800}=-\dfrac{4949}{3960}\)

Sửa đề: `x/2 = y/3` và `xy = 54`

Đặt `x/2 = y/3 = k`

`=> {(x = 2k),(y=3k):}`

Khi đó: `(2k)(3k) = 54`

`<=> 6k^2 = 54`

`<=> k^2 = 9`

`<=> k^2 = 3^2`

`<=> k = -3` hoặc `k = 3`

Xét `k = -3: `

`x = -3.2 = -6`

`y = -3.3 = -9`

Xét `k = 3: `

`x = 3.2 = 6`

`y = 3.3 = 9`

Vậy ...

a, Diện tích xung quanh bể cá dạng hình hộp chữ nhật là:

\(2\cdot\left(4+5\right)\cdot10=180\left(cm^2\right)\)

Diện tích toàn phần bể cá dạng hình hộp chữ nhật là:

\(180+2\cdot4\cdot5=220\left(cm^2\right)\)

Thể tích bể cá dạng hình hộp chữ nhật là:

\(4\cdot5\cdot10=200\left(cm^3\right)\)

b, Diện tích xung quanh khi đổ nước vào bể cao 8 cm là:

\(2\cdot\left(4+5\right)\cdot8=144\left(cm^2\right)\)

Diện tích toàn phần khi đổ nước vào bể cao 8 cm là:

\(144+2\cdot4\cdot5=184\left(cm^2\right)\)

Thể tích khi đổ nước vào bể cao 8 cm là:

\(4\cdot5\cdot8=160\left(cm^3\right)\)

c, Thể tích phần không chứa nước là:

\(200-160=40\left(cm^2\right)\)

d, Tổng thể tích sau khi bỏ đá là:

\(160+100=260\left(cm^3\right)\)

Nước tràn ra ngoài là:

\(260-200=60\left(cm^3\right)\)

a) Diện tích xung quanh của bể cá là:

\(\left(4+5\right)\times2\times10=180\left(cm^2\right)\)

Diện tích toàn phần của bể cá là: 

\(180+2\times4\times5=220\left(cm^2\right)\) 

Thể tích của bể là:

\(4\times5\times10=200\left(cm^3\right)\) 

b) Diện tích xung quanh:

\(\left(4+5\right)\times2\times8=144\left(cm^2\right)\)

Diện tích toàn phần:

\(144+2\times4\times5=184\left(cm^2\right)\)

Thể tích của nước có trong bể:

\(4\times5\times8=160\left(cm^3\right)\) 

c) Diện tích phần không có nước là:

`200-160=40(cm^3)` 

d) Khi bỏ cục đá vào thì thể tích của nước và cục đá là:

\(100+160=260\left(cm^2\right)\) 

Vì: `260>200`

`=>` Nước bị tràn ra ngoài 

Thể tích nước bị tràn là:

`260-200=60(cm^3)`