Cho |x|=|y| và x>0; y<0. Tính giá trị biểu thức 2x+y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(70,08dm^2=700800mm^2\)
\(0,0030hm^2=30m^2\)
10,07kg=10070g
5,06 tấn=5 tấn 600hg

a: \(A=1+2+2^2+...+2^{100}\)
=>\(2A=2+2^2+2^3+...+2^{101}\)
=>\(2A-A=2+2^2+...+2^{101}-1-2-...-2^{100}\)
=>\(A=2^{101}-1\)
b: Đặt \(B=5+5^3+...+5^{99}\)
=>\(25B=5^3+5^5+...+5^{101}\)
=>\(25B-B=5^3+5^5+...+5^{101}-5-5^3-...-5^{99}\)
=>\(24B=5^{101}-5\)
=>\(B=\dfrac{5^{101}-5}{24}\)

Đặt \(A=\dfrac{1}{40}+\dfrac{1}{80}+\dfrac{1}{160}+\dfrac{1}{320}+\dfrac{1}{640}\)
=>\(2A=\dfrac{1}{20}+\dfrac{1}{40}+\dfrac{1}{80}+\dfrac{1}{160}+\dfrac{1}{320}\)
=>\(2A-A=\dfrac{1}{20}+\dfrac{1}{40}+\dfrac{1}{80}+\dfrac{1}{160}+\dfrac{1}{320}-\dfrac{1}{40}-\dfrac{1}{80}-...-\dfrac{1}{640}\)
=>\(A=\dfrac{1}{20}-\dfrac{1}{640}=\dfrac{31}{640}\)

\(\left(1+2+3+...+100\right)\left(1^2+2^2+3^2+...+100^2\right)\left(65\cdot111-13\cdot15\cdot37\right)\)
\(=\left(1+2+...+100\right)\left(1^2+2^2+...+100^2\right)\left[13\cdot37\left(5\cdot3-15\right)\right]\)
=0

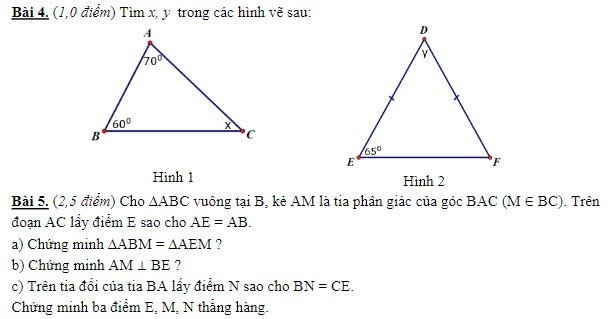
Bài 4
Hình 1: Xét ΔABC có \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
=>\(x+70^0+60^0=180^0\)
=>\(x=50^0\)
Hình 2: Xét ΔDEF có DE=DF
nên ΔDEF cân tại D
=>\(\widehat{EDF}=180^0-2\cdot\widehat{DEF}\)
=>\(y=180^0-2\cdot65^0=50^0\)
Bài 5:
a: Xét ΔABM và ΔAEM có
AB=AE
\(\widehat{BAM}=\widehat{EAM}\)
AM chung
Do đó: ΔABM=ΔAEM
b: ΔABM=ΔAEM
=>MB=ME
=>M nằm trên đường trung trực của BE(1)
Ta có: AB=AE
=>A nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra AM là đường trung trực của BE
=>AM\(\perp\)BE
c: Xét ΔMBN vuông tại B và ΔMEC vuông tại E có
MB=ME
BM=EC
Do đó: ΔMBN=ΔMEC
=>\(\widehat{BMN}=\widehat{EMC}\)
mà \(\widehat{EMC}+\widehat{EMB}=180^0\)(hai góc kề bù)
nên \(\widehat{BMN}+\widehat{BME}=180^0\)
=>E,M,N thẳng hàng

\(a,A=x^2+y^2+2x-6y-2\\ =\left(x^2+2x+1\right)+\left(y^2-6y+9\right)-12\\ =\left(x+1\right)^2+\left(y-3\right)^2-12\)
Ta có:
`(x+1)^2>=0` với mọi x
`(y-3)^2>=0` với mọi y
`=>A=(x+1)^2+(y-3)^2-12>=-12` với mọi x,y
Dấu "=" xảy ra: `x+1=0` và `y-3=0`
`<=>x=-1` và `y=3`
\(b,B=5x^2+y^2+z^2+4xy+2xz\\ =\left(4x^2+4xy+y^2\right)+\left(x^2+2xz+z^2\right)\\ =\left(2x+y\right)^2+\left(x+z\right)^2\)
Ta có:
`(2x+y)^2>=0` với mọi x,y
`(x+z)^2>=0` với mọi x,z
`=>B=(2x+y)^2+(x+z)^2>=0`
Dấu "=" xảy ra: `2x+y=0` và `x+z=0`
`<=>2x=-y=-2z`
\(c,C=2x^2+y^2+2xy-8x+2024\\ =\left(x^2+2xy+y^2\right)+\left(x^2-8x+16\right)+2008\\ =\left(x+y\right)^2+\left(x-4\right)^2+2008\)
Ta có:
`(x+y)^2>=0` với mọi x,y
`(x-4)^2>=0` với mọi x
`=>C=(x+y)^2+(x-4)^2+2008>=2008`
Dấu "=" xảy ra:
`x+y=0` và `x-4=0`
`<=>x=4` và `y=-4`
\(d,D=x^2-2xy+3y^2-2x+1997\\ =\left(x^2+y^2+1-2xy-2x+2y\right)+\left(2y^2-2y+\dfrac{1}{2}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y^2-y+\dfrac{1}{4}\right)+\dfrac{3991}{2}\\ =\left(-x+y+1\right)^2+2\left(y-\dfrac{1}{2}\right)^2+\dfrac{3991}{2}\)
Ta có:
`(-x+y+1)^2>=0` với mọi x,y
`2(y-1/2)^2>=0` với mọi y
`=>D=(-x+y+1)^2+2(y-1/2)^2+3991/2>=3991/2`
Dấu "=" xảy ra: `-x+y+1=0` và `y-1/2=0`
`<=>y=1/2` và `x=3/2`

\(1/\left(x+5\right)\left(x^2-4\right)=0\\ TH1:x+5=0\\ =>x=-5\\ TH2:x^2-4=0\\ =>x^2=4\\ =>x^2=\left(\pm2\right)^2\\ =>x=\pm2\\ 2/3x-10=2x+13\\ =>3x-2x=13+10\\ =>x=23\\ 3/3\left(4-x\right)-2\left(x-1\right)=x+2\\ =>12-3x-2x+2=x+2\\ =>14-5x=x+2\\ =>x+5x=14-2\\ =>6x=12\\ =>x=\dfrac{12}{6}=2\\ 4/2\left(x-1\right)+3\left(x-2\right)=x-4\\ =>2x-2+3x-6=x-4\\ =>5x-8=x-4\\ =>5x-x=-4+8\\ =>4x=4\\ =>x=\dfrac{4}{4}=1\\ 5/4\left(2x+7\right)-3\left(3x-2\right)=24\\ =>8x+28-9x+6=24\\ =>34-x=24\\ =>x=34-24=10\\ 6/6x+23=2x-12\\ =>6x-2x=-12-23\\ =>4x=-35\\ =>x=\dfrac{-35}{4}\)

Thương là 3
=> Số lớn gấp 3 lần số bé
=> Coi số bé là 1 phần số lớn là 3 phần
Tổng số phần bằng nhau là:
3 + 1 = 4 (phần)
Số bé là:
3 : 4 x 1 = `3/4`
Số lớn là:
`3-3/4=9/4`
ĐS: ...

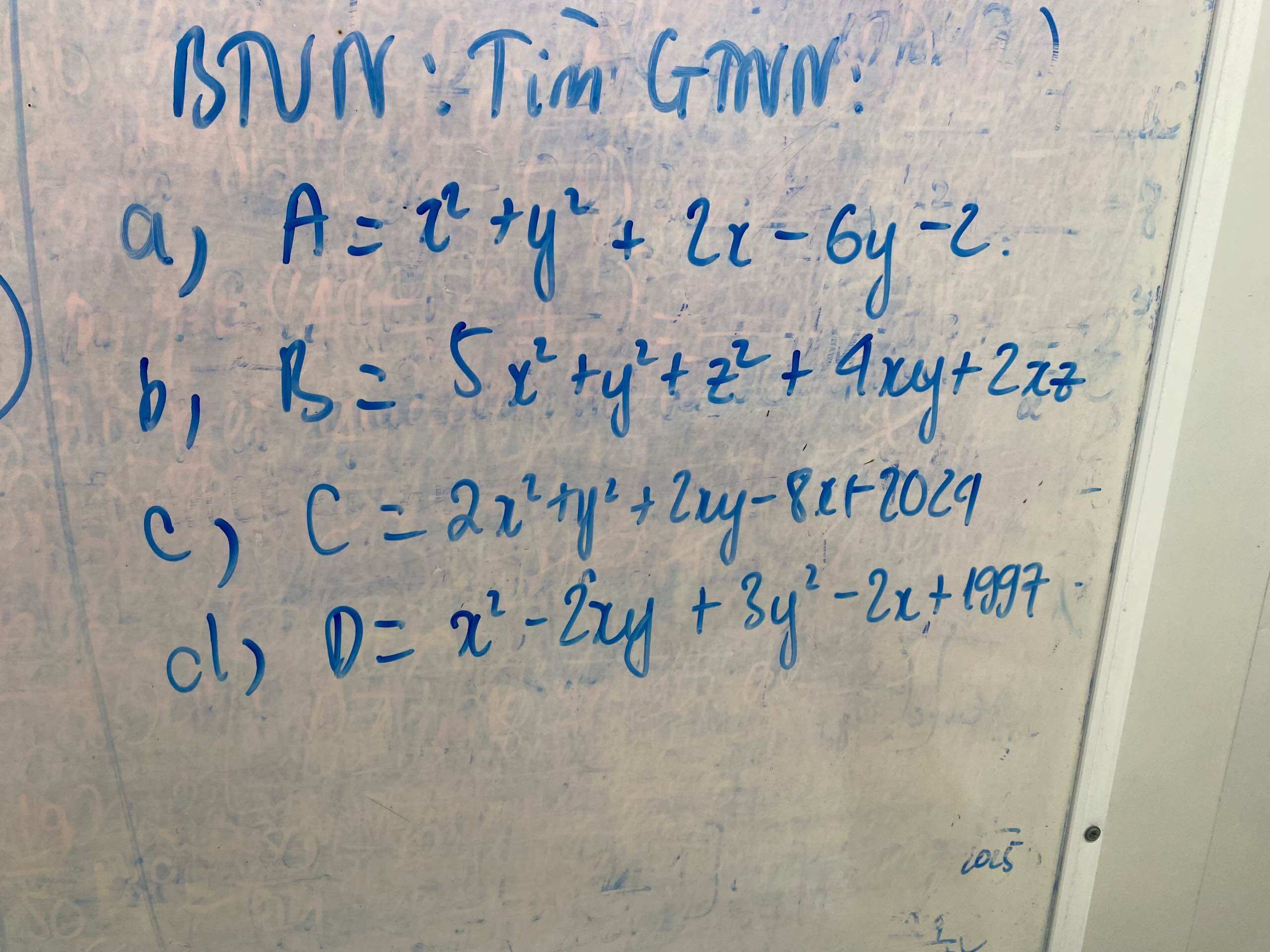
|x|=|y|
mà x>0; y<0
nên x=-y
2x+y=-2y+y=-y
\(\left|x\right|=\left|y\right|\) và \(x>0;y< 0\)
\(\Rightarrow y=-x\)
\(\Rightarrow2x\pm x=x\)
Vậy \(2x+y=x\)