rhqeuhfjaebg
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


38 tấn 270kg=38270kg
Trong 5 tháng tiếp theo, cửa hàng bán được:
7905x5=39525(kg)
Số lượng gạo cửa hàng bán được trong 10 tháng là:
38270+39525=77795(kg)

a: Bạn ghi lại đề nhé
b: Xét ΔBAH và ΔBDH có
BA=BD
AH=DH
BH chung
Do đó: ΔBAH=ΔBDH
=>\(\widehat{ABH}=\widehat{DBH}\)
Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
c: Ta có: ΔBAE=ΔBDE
=>\(\widehat{BAE}=\widehat{BDE}=90^0\)
=>DE\(\perp\)BC
Ta có: EA=ED
mà EM>EA(ΔEAM vuông tại A)
nên EM>ED
d: Đề sai rồi bạn

1: \(\dfrac{2x+1}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\dfrac{2x+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
\(=\dfrac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}-1}\)
\(\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)\)
\(=\dfrac{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}+x\right)}{1+\sqrt{x}}-\sqrt{x}\)
\(=1-\sqrt{x}+x-\sqrt{x}=x-2\sqrt{x}+1=\left(\sqrt{x}-1\right)^2\)
\(B=\left(\dfrac{2x+1}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}-1}+\dfrac{2-2\sqrt{x}}{\sqrt{x}}\)
\(=\sqrt{x}-1+\dfrac{2-2\sqrt{x}}{\sqrt{x}}=\dfrac{x-\sqrt{x}+2-2\sqrt{x}}{\sqrt{x}}\)
\(=\dfrac{x-3\sqrt{x}+2}{\sqrt{x}}=\left(\sqrt{x}-1\right)\cdot\dfrac{\left(\sqrt{x}-2\right)}{\sqrt{x}}\)
2:
a:
Để B=0 thì \(\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\sqrt{x}}=0\)
=>\(\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)=0\)
=>\(\left[{}\begin{matrix}x=1\left(loại\right)\\x=4\left(nhận\right)\end{matrix}\right.\)
b: \(B+\dfrac{3\sqrt{x}-4}{\sqrt{x}}< =0\)
=>\(\dfrac{x-3\sqrt{x}+2+3\sqrt{x}-4}{\sqrt{x}}< =0\)
=>x-2<=0
=>x<=2
kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}0< x< =2\\x\ne1\end{matrix}\right.\)
3: Để B là số nguyên thì \(x-3\sqrt{x}+2⋮\sqrt{x}\)
=>\(\sqrt{x}\left(\sqrt{x}-3\right)+2⋮\sqrt{x}\)
=>\(2⋮\sqrt{x}\)
=>\(\sqrt{x}\in\left\{1;2\right\}\)
=>\(x\in\left\{1;4\right\}\)
Kết hợp ĐKXĐ, ta được: x=4

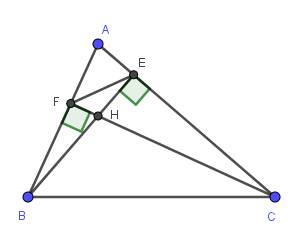
a) Xét hai tam giác vuông: \(\Delta BHF\) và \(\Delta CHE\) có:
\(\widehat{BHF}=\widehat{CHE}\) (đối đỉnh)
\(\Rightarrow\Delta BHF\) ∽ \(\Delta CHE\) (g-g)
\(\Rightarrow\dfrac{HB}{HC}=\dfrac{HF}{HE}\)
\(\Rightarrow HE.HB=HC.HF\)
b) Xét hai tam giác vuông: \(\Delta AFC\) và \(\Delta AEB\) có:
\(\widehat{A}\) chung
\(\Rightarrow\Delta AFC\) ∽ \(\Delta AEB\) (g-g)
\(\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\)
\(\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC\) có:
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
\(\Rightarrow\Delta AEF\) ∽ \(\Delta ABC\) (c-g-c)

a: Ta có: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-35^0=55^0\)
b: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
Do đó; ΔBAE=ΔBDE
c: Ta có: ΔBAE=ΔBDE
=>EA=ED
Xét ΔEAK vuông tại A và ΔEDC vuông tại D có
EA=ED
\(\widehat{AEK}=\widehat{DEC}\)(hai góc đối đỉnh)
Do đó: ΔEAK=ΔEDC
=>EK=EC

\(2xy+y-14=4x\)
\(4x-2xy-y+14=0\)
\(\left(4x-2xy\right)-y=-14\)
\(2x\left(2-y\right)+2-y=-14+2\)
\(2x\left(2-y\right)+\left(2-y\right)=-12\)
\(\left(2-y\right)\left(2x+1\right)=-12\)
Mà \(x,y\in Z\)
\(2x+1\) là số nguyên lẻ
\(\Rightarrow2x+1\in\left\{-3;-1;1;3\right\}\)
\(\Rightarrow2x\in\left\{-4;-2;0;2\right\}\)
\(\Rightarrow x\in\left\{-2;-1;0;1\right\}\)
*) \(x=-2\)
\(\Rightarrow\left(2-y\right)\left[2.\left(-2\right)+1\right]=-12\)
\(\Rightarrow\left(2-y\right).\left(-3\right)=-12\)
\(\Rightarrow2-y=4\)
\(\Rightarrow y=-2\)
\(\Rightarrow\left(x;y\right)=\left(-2;-2\right)\)
*) \(x=-1\)
\(\Rightarrow\left(2-y\right)\left[2.\left(-1\right)+1\right]=-12\)
\(\Rightarrow\left(2-y\right).\left(-1\right)=-12\)
\(\Rightarrow2-y=12\)
\(\Rightarrow y=-10\)
\(\Rightarrow\left(x;y\right)=\left(-1;-10\right)\)
*) \(x=1\)
\(\Rightarrow\left(2-y\right)\left(2.1+1\right)=-12\)
\(\Rightarrow\left(2-y\right).3=-12\)
\(\Rightarrow2-y=-4\)
\(\Rightarrow y=6\)
\(\Rightarrow\left(x;y\right)=\left(1;6\right)\)
*) \(x=0\)
\(\Rightarrow\left(2-y\right)\left(2.0+1\right)=-12\)
\(\Rightarrow\left(2-y\right).1=-12\)
\(\Rightarrow2-y=-12\)
\(\Rightarrow y=14\)
\(\Rightarrow\left(x;y\right)=\left(0;14\right)\)
Vậy \(\left(x;y\right)\in\left\{\left(-2;-2\right);\left(-1;-10\right);\left(-2;-2\right);\left(0;14\right)\right\}\)
Olm chào em, đây là dạng toán nâng cao chuyên đề giải phương trình nghiệm nguyên, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay Olm sẽ hướng dẫn các em giải dạng này như sau:
Giải:
2\(xy\) + y - 14 = 4\(x\)
(2\(xy\) + y) - 14 = 4\(x\)
y(2\(x\) + 1) = 4\(x\) + 14
y = (4\(x\) + 14) : (2\(x\) + 1)
y \(\in\) Z ⇔ (4\(x\) + 14) ⋮ (2\(x\) + 1)
⇒ (4\(x\) + 2 + 12) ⋮ (2\(x\) + 1)
⇒ [2.(2\(x\) + 1) + 12] ⋮ (2\(x\) + 1)
⇒ 12 ⋮ (2\(x\) + 1)
2\(x\) + 1 \(\in\) Ư(12) = {-12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}
Lập bảng ta có:
| 2\(x\) + 1 | -12 | -6 | -4 | -3 | -2 | -1 | 1 | 2 | 3 | 4 | 6 | 12 |
| \(x\) | -\(\dfrac{13}{2}\) | - \(\dfrac{5}{2}\) | \(\dfrac{-3}{2}\) | -2 | \(\dfrac{-3}{2}\) | -1 | 0 | \(\dfrac{1}{2}\) | 1 | \(\dfrac{5}{2}\) | \(\dfrac{5}{2}\) | \(\dfrac{11}{2}\) |
| y = \(\dfrac{4x+14}{2x+1}\) | -2 | -10 | 14 | 6 | ||||||||
| \(x;y\in\) Z | loại | loại | loại | loại | loại | loại | loại | loại |
Theo bảng trên ta có: (\(x\); y) = (-2; -2); (-1; -10); (0; 14); (1; 6)
Kết luận: Các cặp \(x;y\) nguyên thỏa mãn đề bài là:
(\(x;y\)) = (-2; -2); (-1; -10); (0; 14); (1; 6)

Số học sinh giỏi:
\(45.\dfrac{1}{5}=9\) (học sinh)
Số học sinh khá:
\(45.\dfrac{2}{15}=6\) (học sinh)
Số học sinh trung bình:
\(\left(9+6\right).60\%=9\) (học sinh)
Số học sinh yếu:
\(45-9-6-9=21\) (học sinh)


(- \(\dfrac{2}{5}\))2 + \(\dfrac{1}{2}\) x (4,5 - 2) - 25%
= \(\dfrac{4}{25}\) + \(\dfrac{1}{2}\) x 2,5 - 0,25
= 0,16 + 1,25 - 0,25
= 0,16 + (1,25 - 0,25)
= 0,16 + 1
= 1,16

hết cái bọn hoàng văn thụ r đến cái bọn victory.
bạn bị khùng à? không phải mình nói xấu bạn mà bạn đang quấy rối đấy