 giải hộ em với
giải hộ em với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(1-\frac{1}{8}\)\(-\frac{1}{6}\)\(=\frac{24}{24}\)\(-\frac{3}{24}\)\(-\frac{4}{24}\)\(=\frac{17}{24}\)


3 - 1 = 2
0 + 5 =5
1 + 1 + 3 =5
2 + 3 = 5
3 - 2 = 1
2 + 2 + 1 =5
4 + 0 =4
3 + 1 + 0 =4

\(x^2\)\(+x-2022x-2022=0\)
\(x\left(x-2022\right)\)\(+\left(x-2022\right)\)\(=0\)
\(\left(x-2022\right)\)\(\left(x+1\right)\)\(=0\)
\(=>TH1:x-2022=0\)
\(=>x=2022\)
\(TH2:x-1=0\)
\(=>x=-1\)
Đặt A(x)=x2−2021x+2020=0A(x)=x2−2021x+2020=0
⇔x2−2020x−x+2020=0⇔x2−2020x−x+2020=0
⇔x(x−1)−2020(x−1)=0⇔x(x−1)−2020(x−1)=0
⇔(x−2020)(x−1)=0⇔x=\orbr{x=2020x=1⇔(x−2020)(x−1)=0⇔x=\orbr{x=2020x=1
Vậy nghiệm của phương trình là x = 1 ; x = 2020

Hàm số y=m−3.x+23 là hàm số bậc nhất khi hệ số của x là a=m−3≠0
Ta có: m−3≠0⇔m−3>0⇔m>3
Vậy khi m>3 thì hàm số y=m−3x+23 là hàm số bậc nhất
Câu b
S=1m+2t−34 (t là biến số).
Phương pháp giải:
Để hàm số được cho bởi công thức y=ax+b là hàm số bậc nhất thì a≠0 .
Lời giải chi tiết:
Hàm số S=1m+2t−34 là hàm số bậc nhất khi hệ số của t là a=1m+2≠0
Ta có: 1m+2≠0⇔m+2≠0⇔m≠−2
Vậy khi m≠−2 thì hàm số S=1m+2t−34 là hàm số bậc nhất.
Lời giải và đáp án
Đây là dạng toán hàm số bậc nhất nha bạn, áp dụng vào và làm là được!
\(a.\)\(\text{Hàm số }y=(\sqrt{m-3)}x+\frac{2}{3}\) \(\text{là hàm số bậc nhất khi hệ số của }\)\(x\)\(\text{là}\)\(a=\sqrt{m-3\ne}0\)
\(\text{Ta có: }\sqrt{m-3}m-3\ne0\Leftrightarrow m-3>0\Leftrightarrow m>3\)
\(\text{Vậy khi}\) \(m>3\)\(\text{thì hàm số }y=(\sqrt{m-3})x+\frac{2}{3}\text{ là hàm số bậc nhất.}\)
\(b.\) \(\text{Hàm số }S=:\frac{1}{m+2}t-\frac{3}{4}\text{là hàm số bậc nhất khi hệ số của }t\text{ là }a=:\frac{1}{m+2}\ne0\)
\(\text{Ta có: }\frac{1}{m+2}\ne0\Leftrightarrow m+2\ne0\Leftrightarrow m\ne-2\)
\(\text{Vậy khi}\) \(m\ne-2\text{thì hàm số}\)\(S=:\frac{1}{m+2}t-\frac{3}{4}\text{là hàm số bậc nhất.}\)

csc(-x) = -csc(x) cos(-x) = cos(x) sec(-x) = sec(x) tan(-x) = -tan(x) cot(-x) = -cot(x)
tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos^2(x) - sin^2(x) = 2 cos^2(x) - 1 = 1 - 2 sin^2(x) tan(2x) = 2 tan(x) / (1 - tan^2(x)) sin^2(x) = 1/2 - 1/2 cos(2x) cos^2(x) = 1/2 + 1/2 cos(2x) sin x - sin y = 2 sin( (x - y)/2 ) cos( (x + y)/2 ) cos x - cos y = -2 sin( (x - y)/2 ) sin( (x + y)/2 )
a/sin(A) = b/sin(B) = c/sin(C) (Law of Sines)
(a - b)/(a + b) = tan [(A-B)/2] / tan [(A+B)/2] (Law of Tangents) | |||||||||||||||||||||||||||||||||||||||||||

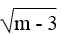 )x + 2/3
)x + 2/3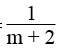 t - 3/4 (t là biến số)
t - 3/4 (t là biến số)
8) \(\frac{x}{3}=\frac{y}{2}=\frac{2x+5y}{2.3+5.2}=\frac{32}{16}=2\)
\(\Leftrightarrow\hept{\begin{cases}x=2.3=6\\y=2.2=4\end{cases}}\)
9) \(\frac{x}{y}=\frac{3}{16}\Leftrightarrow\frac{x}{3}=\frac{y}{16}=\frac{3x-y}{3.3-16}=\frac{35}{-7}=-5\)
\(\Leftrightarrow\hept{\begin{cases}x=-5.3=-15\\y=-5.16=-80\end{cases}}\)
10) \(3x=5y\Leftrightarrow\frac{x}{5}=\frac{y}{3}=\frac{x+y}{5+3}=\frac{40}{8}=5\)
\(\hept{\begin{cases}x=5.5=25\\y=5.3=15\end{cases}}\)