4x - 8 = 12
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ: $x\notin\{-5;-4;-3\}$
$\frac{1}{x+5}+\frac{2}{x+4}+\frac{3}{x+3}+3=0$
$\Leftrightarrow \left(\frac{1}{x+3}+1\right)+\left(\frac{2}{x+4}+1\right)+\left(\frac{3}{x+3}+1\right)=0$
$\Leftrightarrow \frac{x+6}{x+5}+\frac{x+6}{x+4}+\frac{x+6}{x+3}=0$
$\Leftrightarrow (x+6)\left(\frac{1}{x+5}+\frac{1}{x+4}+\frac{1}{x+3}\right)=0$
+, TH1: $x+6=0\Leftrightarrow x=-6$ (tm ĐKXĐ)
+, TH2: $\frac{1}{x+5}+\frac{1}{x+4}+\frac{1}{x+3}=0$
$\Leftrightarrow \frac{(x+4)(x+3)+(x+3)(x+5)+(x+4)(x+5)}{(x+3)(x+4)(x+5)}=0$
$\Rightarrow 3x^2+24x+47=0$
$\Leftrightarrow \left[\begin{array}{}x =\frac{-12+\sqrt3}{3}(TM) \\x=\frac{-12-\sqrt3}{3}(TM) \end{array}\right. $
$\text{#}Toru$
ĐKXĐ: \(x\notin\left\{-5;-4;-3\right\}\)
\(\dfrac{1}{x+5}+\dfrac{2}{x+4}+\dfrac{3}{x+3}+3=0\)
=>\(\left(\dfrac{1}{x+5}+1\right)+\left(\dfrac{2}{x+4}+1\right)+\left(\dfrac{3}{x+3}+1\right)=0\)
=>\(\dfrac{x+6}{x+5}+\dfrac{x+6}{x+4}+\dfrac{x+6}{x+3}=0\)
=>\(\left(x+6\right)\left(\dfrac{1}{x+5}+\dfrac{1}{x+4}+\dfrac{1}{x+3}\right)=0\)
=>x+6=0
=>x=-6(nhận)

12 - 4 = 8
12 - (-4) = 12 + 4 = 16
-12 - (-4) = -12 + 4 = -8
12 + (-4) = 12 - 4 = 8
15 - (-5) = 15 + 5 = 20
12 - 4 = 8
12 - ( -4) = 12 + 4 = 16
-12 - ( -4) = -12 + 4 = - ( 12 - 4 ) = -8
12 + ( -4) = 12 - 4 =8
15 - ( -5) = 15 + 5 =20

32.5 - 22.7 + 83
= 9.5 - 4.7 + 83
= 45 - 28 + 83
= 17 + 83
= 100

9+2 = 11
12 + 3 = 15
10 - 1 = 9
21 - 11 = 10
(- 2) - (- 3) = (- 2) + 3 = 1

a: \(-\dfrac{9}{4}=-2,25\)
mà -2,25<-2,12
nên \(-\dfrac{9}{4}< -2,12\)
b: \(-1\dfrac{1}{5}=-1,2\)
mà -1,2>-1,75
nên \(-1\dfrac{1}{5}>-1,75\)
c:

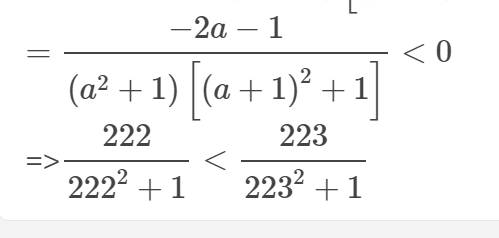

Bài 1
a) 3,6 : 1,2 . 3 + 5 . 10 : 2 - 4
= 3 . 3 + 50 : 2 - 4
= 9 + 25 - 4
= 34 - 4
= 30
b)
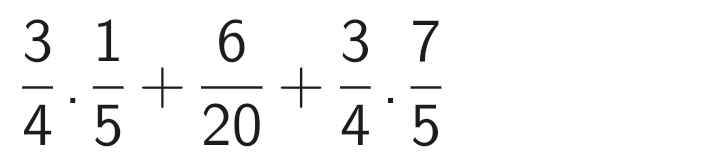
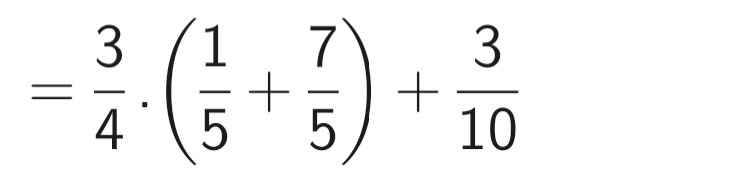
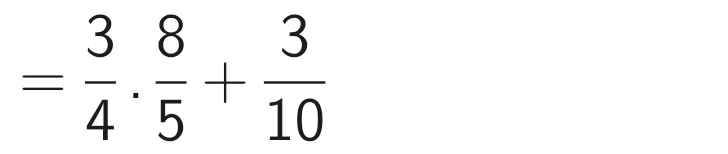



\(\left(\dfrac{1}{2}x+2\right)\left(x^2+\dfrac{1}{4}\right)=0\)
mà \(x^2+\dfrac{1}{4}>=\dfrac{1}{4}>0\forall x\)
nên \(\dfrac{1}{2}x+2=0\)
=>\(\dfrac{x}{2}=-2\)
=>x=-4
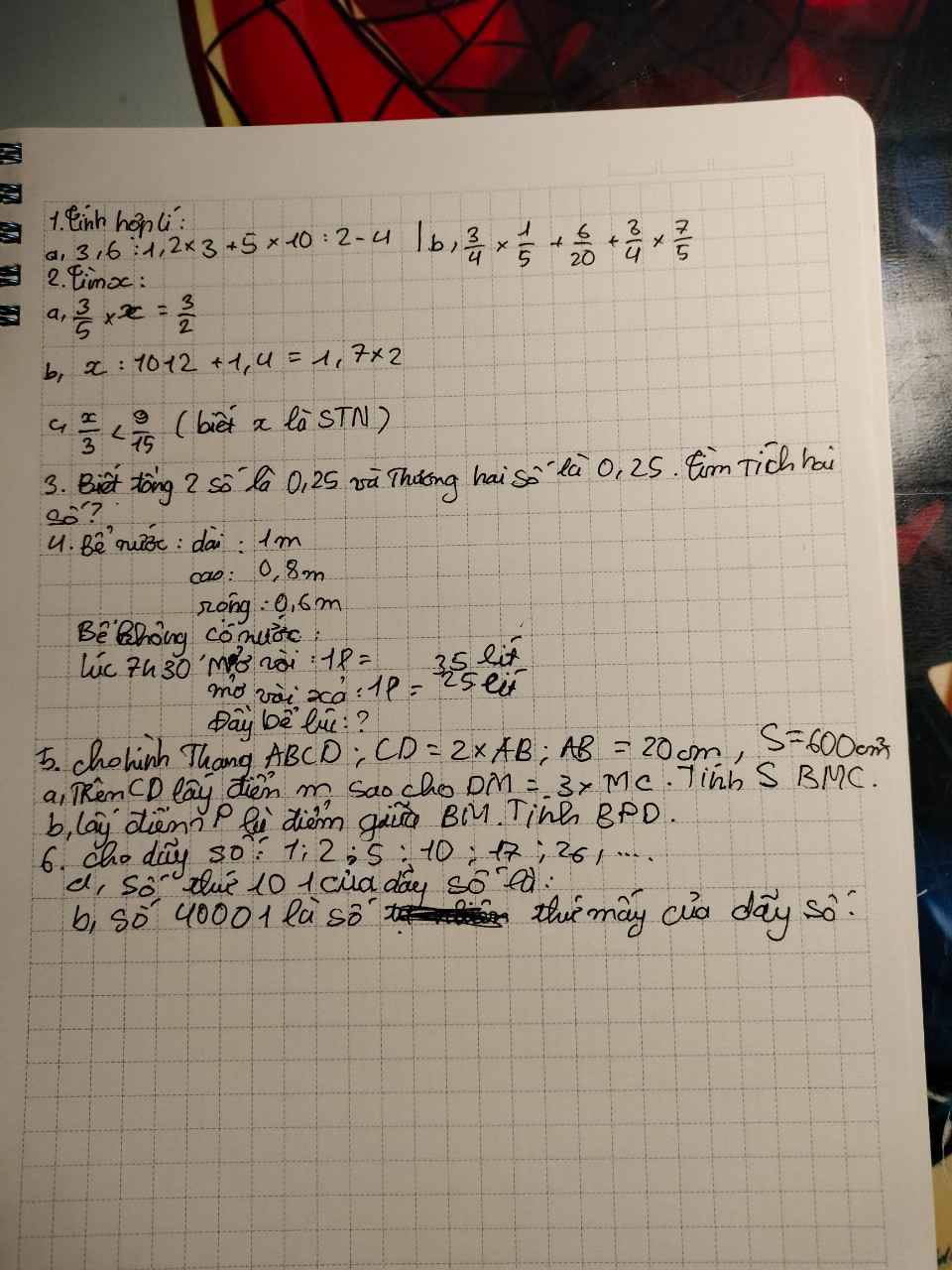
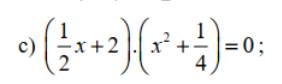
giải
4x = 12+8
4x = 20
x = 20 chia 4
x = 5
`4x-8=12`
`=> 4x=12+8`
`=>4x=20`
`=>x=20/4`
`=>x=5`