a: Xét ΔBAM vuông tại A và ΔBKM vuông tại K có

BM chung

\(\widehat{ABM}=\widehat{KBM}\)

Do đó: ΔBAM=ΔBKM

=>BA=BK

=>ΔBAK cân tại B

b: Ta có: \(\widehat{CAK}+\widehat{BAK}=\widehat{BAC}=90^0\)

\(\widehat{DAK}+\widehat{BKA}=90^0\)(ΔDAK vuông tại D)

mà \(\widehat{BAK}=\widehat{BKA}\)(ΔBAK cân tại B)

nên \(\widehat{CAK}=\widehat{DAK}\)

=>AK là phân giác của góc DAC

c: Xét ΔABC vuông tại A có AD là đường cao

nên \(AD\cdot BC=AB\cdot AC\)

\(\left(AB+AC\right)^2-\left(BC+AD\right)^2\)

\(=AB^2+AC^2+2\cdot AB\cdot AC-BC^2-2\cdot BC\cdot AD-AD^2\)

\(=BC^2+2\cdot BC\cdot AD-BC^2-2\cdot BC\cdot AD-AD^2\)

\(=-AD^2< 0\)

=>\(\left(AB+AC\right)^2< \left(BC+AD\right)^2\)

=>AB+AC<BC+AD

Ta thực hiện theo các bước sau:

Bước 1. Xác định ba điểm A, B, C nằm trên rìa mảnh gỗ .

Bước 2. Xác định ba đường trung trực của tam giác ABC.

Bước 3. Xác định giao điểm của ba đường trung trực của tam giác ABC.

Điểm đó là tâm của mảnh gỗ

Cái  thì tui chịu

Sửa đề:

ABC cân tại A có BH và CK là hai đường cao

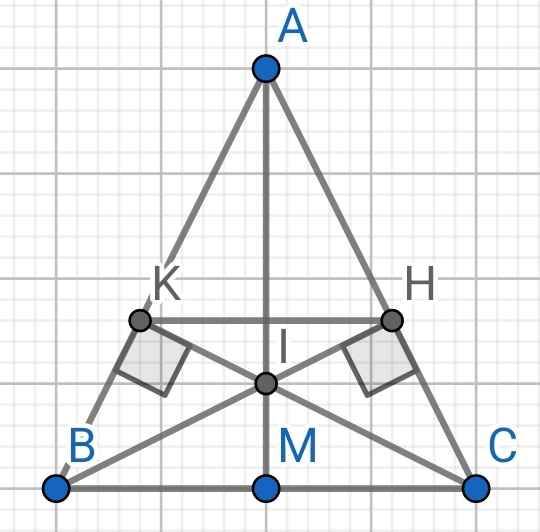
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆AHB và ∆AKC có:

AB = AC (cmt)

∠A chung

⇒ ∆AHB = ∆AKC (cạnh huyền - góc nhọn)

⇒ AH = AK (hai cạnh tương ứng)

⇒ ∆AKH cân tại A

b) ∆ABC cân tại A (gt)

BH và CK là hai đường cao cắt nhau tại I (gt)

⇒ AI là đường cao thứ ba

⇒ AI ⊥ BC

⇒ IM ⊥ BC

Do ∆ABC cân tại A có

AI là đường cao (cmt)

⇒ AM là đường cao

⇒ AM cũng là đường trung tuyến

⇒ M là trung điểm của BC

⇒ MB = MC

Xét hai tam giác vuông: ∆IBM và ∆ICM có:

IM là cạnh chung

MB = MC (cmt)

⇒ ∆IBM = ∆ICM (hai cạnh góc vuông)

⇒ ∠BIM = ∠CIM (hai góc tương ứng)

⇒ IM là tia phân giác của ∠BIC

c) Xét hai tam giác vuông: ∆AHI và ∆AKI có:

AI là cạnh chung

AH = AK (cmt)

⇒ ∆AHI = ∆AKI (cạnh huyền - cạnh góc vuông)

⇒ IH = IK (hai cạnh tương ứng)

⇒ I nằm trên đường trung trực của HK (1)

Do AH = AK (cmt)

⇒ A nằm trên đường trung trực của HK (2)

Từ (1) và (2) ⇒ AI là đường trung trực của HK

⇒ AI ⊥ HK

Lại có:

AI ⊥ BC (cmt)

⇒ HK // BC

\(\left(x+3\right)\left(x-1\right)=x\left(x-1\right)+3\left(x-1\right)=x^2-x+3x-3=x^2+2x-3\)

\(\left(3x^3-2x^2\right):3x^2=3x^3:3x^2-2x^2:3x^2=x-\dfrac{2}{3}\)

40 km/giờ

mình có bài này bạn lấy thâm khảo nhé nhớ cho mình một like ( •̀ ω •́ )✧

Trong cùng 1 quãng đường AB,vận tốc và thời gian là 2 đại lượng tỉ lê nghịch.Vậy tỉ số thời gian đi với vận tốc 20km/giờ=3/2 thời gian đi với vận tốc 30km/giờ.

Coi...

Thời gian đi với vận tốc 20km/giờ là:

2:(3-2)*3=6(giờ)

Quãng đường AB là:

20*6=120(km)

Đáp số:120km

-123,49

-123.5

Tổng của số bị trừ và số trừ là 3600-1550=2050

Hiệu của số bị trừ và số trừ là 1550

Số bị trừ là (2050+1550):2=3600:2=1800

Số trừ là 1800-1550=250

Tổng của số bị trừ và số trừ là:

3600-1550=2050

Hiệu của số bị trừ và số trừ là:

1550

Số bị trừ là:

(2050+1550):2=3600:2=1800

Số trừ là:

1800-1550=250