chứng minh rằng tồn tại một bội của 2023 có dạng 202420242024...2024
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét 2024 số:
\(a_1=2024\)
\(a_2=20242024\)
\(a_3=202420242024\)
...
\(a_{2024}=20242024...2024\) (2024 lần cụm "2024")
Một số khi chia cho 2023 thì có 2023 số dư phân biệt là 0, 1, 2,..., 2023
\(\Rightarrow\) Theo nguyên lí Dirichlet tồn tại 2 số \(a_i,a_j\left(i\ne j,1\le i< j\le2024\right)\) trong số 2024 số kể trên có cùng số dư khi chia cho 2023.
\(\Rightarrow a_j-a_i⋮2023\)
\(\Rightarrow20242024...2024-20242024...2024⋮2023\)
(\(j\) cụm "2024) (\(i\) cụm "2024)
\(\Rightarrow20242024...2024000...00⋮2023\)
(\(j-i\) cụm "2024" và \(i\) chữ số 0)
\(\Rightarrow20242024...2024.10^i⋮2023\) (*)
Nhưng vì \(10^i=2^i.5^i\) và \(2023=7.17^2\) nên \(ƯCLN\left(10^i,2023\right)=1\)
Từ đó (*) suy ra \(20242024...2024⋮2023\)
(\(j-i\) cụm 2024)
Ta có đpcm.

1 người làm cỏ trên một cánh đồng hết số thời gian là:
10 x 9 = 90 (giờ)
15 người làm cỏ trên một cánh đồng hết số thời gian là:
90 : 15 = 6 (giờ)
Đ/S:... (Cho con GP ạ)
Do năng suất của mỗi người là như nhau và cùng làm cỏ một cánh đồng nên số người và thời gian là hai đại lượng tỉ lệ nghịch
Thời gian 15 người làm cỏ cánh đồng đó:
10 . 9 : 15 = 6 (giờ)

\(B=\dfrac{2n-3}{n-2}=\dfrac{2n-4+1}{n-2}=\dfrac{2\left(n-2\right)}{n-2}+\dfrac{1}{n-2}=2+\dfrac{1}{n-2}\)
Do \(2\in Z\Rightarrow B\in Z\) khi \(\dfrac{1}{n-2}\in Z\)
\(\Rightarrow n-2=Ư\left(1\right)\)
\(\Rightarrow n-2=\left\{-1;1\right\}\)
\(\Rightarrow n=\left\{1;3\right\}\)

Gọi x, y, z(kg) lần lượt là số giấy vụ ba chi đội 7A, 7B và 7C thu được (x, y, z > 0)
Theo đề bài, ta có:
\(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}\) và \(x+y+z=120\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{7}=\dfrac{y}{8}=\dfrac{z}{9}=\dfrac{x+y+z}{7+8+9}=\dfrac{120}{24}=5\)
\(\Rightarrow\left\{{}\begin{matrix}x=5\cdot7=35\\y=5\cdot8=40\\z=5\cdot9=45\end{matrix}\right.\)
Vậy số kg giấy vụn ba chi đội 7A, 7B và 7C thu được lần lượt là 35kg, 40kg và 45kg
Để tính số giấy mỗi chi đội thu được, ta cần chia tổng số giấy vụn (120 kg) theo tỉ lệ 7:8:9 thành 3 phần.
Tổng số phần là 7 + 8 + 9 = 24
Số giấy mỗi chi đội 7A thu được: 120 x (7/24) = 35 kg Số giấy mỗi chi đội 7B thu được: 120 x (8/24) = 40 kg Số giấy mỗi chi đội 7C thu được: 120 x (9/24) = 45 kg
Vậy số giấy mỗi chi đội thu được lần lượt là: 35 kg, 40 kg, 45 kg.

a/\(\dfrac{x}{5}=\dfrac{-3}{15}\)
\(\dfrac{x}{5}=\dfrac{-1}{5}\)
\(x=-1\)
b/Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{17}=\dfrac{y}{12}=\dfrac{x-y}{17-12}=\dfrac{10}{5}=2\)
\(\Rightarrow\left\{{}\begin{matrix}x=2\cdot17=34\\y=2\cdot12=24\end{matrix}\right.\)
a/�5=−3155x=15−3
�5=−155x=5−1
�=−1x=−1
b/Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
�17=�12=�−�17−12=105=217x=12y=17−12x−y=510=2
⇒{�=2⋅17=34�=2⋅12=24⇒{x=2⋅17=34y=2⋅12=24

Ta có: EF song song MN (cùng vuông góc AB)
D là trung điểm OA \(\Rightarrow AD=OD=\dfrac{R}{2}\)
Mà \(AC=OB=R\)
\(\Rightarrow AC+AD=OD+OB\Rightarrow DC=BD\)
Hay D là trung điểm BD
\(\Rightarrow EF\) là đường trung bình tam giác BMN
\(\Rightarrow MN=2EF\)
AB là đường kính và E thuộc đường tròn \(\Rightarrow\widehat{AEB}=90^0\) hay tam giác ABE vuông tại E
Áp dụng hệ thức lượng trong tam giác vuông ABE với đường cao ED:
\(ED^2=AD.DB=AD\left(OD+OB\right)=\dfrac{R}{2}.\left(\dfrac{R}{2}+R\right)=\dfrac{3R^2}{4}\)
\(\Rightarrow ED=\dfrac{R\sqrt{3}}{2}\)
\(\Rightarrow EF=2ED=R\sqrt{3}\)
\(\Rightarrow MN=2EF=2R\sqrt{3}\)
Gọi G là giao điểm của EF và AB. Ta có:
AG = AD + DG = R + R/2 = 3R/2
Vì tam giác ABC vuông tại C nên ta có:
AC^2 + BC^2 = AB^2
R^2 + BC^2 = (2R)^2
BC = R√3
Ta có:
CG = BC - BC/2 = R√3 - R√3/2 = R√3/2
Vì tam giác CGE vuông tại G nên ta có:
GE = CG * tan(∠GCE) = CG * tan(∠CBE)
GE = R√3/2 * tan(∠CBE)
Vì EF vuông góc với AB nên tam giác BEG vuông tại G, ta có:
BG^2 + GE^2 = BE^2
(R/2)^2 + (R√3/2 * tan(∠CBE))^2 = R^2
R^2/4 + 3R^2/4 * tan^2(∠CBE) = R^2
tan^2(∠CBE) = 1/3
tan(∠CBE) = √(1/3)
sin(∠CBE) = 1/√3
MN = 2 * GM = 2 * GE * sin(∠CBE)
MN = 2 * R√3/2 * √(1/3) = R
Vậy độ dài đoạn thẳng MN là R.

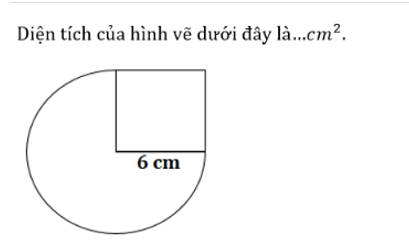
Diện tích hình vuông:
\(6\times6=36\left(cm^2\right)\)
Diện tích hình tròn:
\(6\times6\times3,14=113,04\left(cm^2\right)\)
Diện tích \(\dfrac{3}{4}\) hình tròn:
\(113,04\times\dfrac{3}{4}=84,78\left(cm^2\right)\)
Diện tích hình vẽ:
\(84,78+36=120,78\left(cm^2\right)\)
Đáp số: 120,78 cm2
Diện tích hình vuông là:
\(6\times6=36\left(cm^2\right)\)
Diện tích hình tròn là:
\(6\times6\times3,14=113,04\left(cm^2\right)\)
Diện tích của 3/4 hình tròn là:
\(113,04\times\dfrac{3}{4}=84,78\left(cm^2\right)\)
Diện tích của hình là:
\(36+84,78=120,78\left(cm^2\right)\)

a/Thay x = -6 vào biểu thức, ta có:
\(3\times\left(-6\right)+5\)
\(=-18+5\)
\(=-13\)
b/Thay m = -2 và n = -1 vào biểu thức, ta có:
\(2\cdot\left(-2\right)^2-3\cdot\left(-1\right)+7\)
\(=8+3+7\)
\(=18\)
a.
Tại \(x=-6\Rightarrow3x+5=3.\left(-6\right)+5=-13\)
b.
Tại \(m=-2;n=-1\)
\(2m^2-3n+7=2.\left(-2\right)^2-3.\left(-1\right)+7=18\)
Ta thấy: \(2024\equiv1\) (\(mod\) \(2023\))
\(20242024\equiv1909\) (\(mod\) \(2023\))
...
\(2024...2024:2023\) dư một số nào đó là một trong các số từ \(1\) đến \(2022\) (\(2023\) số).
* Xét \(2024\) số: \(2024;20242024;...;20242024...2024\) (Gồm \(2024\) bộ số \(2024\))
+ Lấy \(2024\) số trên chia cho \(2023\), ta có \(2024\) số dư từ \(0\) đến \(2022\).
\(\Rightarrow\) Tồn tại hai số chia cho \(2023\) có cùng số dư.
Giả sử hai số đó là \(a=2024...2024\) (\(i\) bộ số \(2024\)) và \(b=2024...2024\) (\(j\) bộ số \(2024\)) \(\left(1\le i\le j\le2024\right)\)
+ \(a-b=2024...2024\cdot10^{4i}\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\)
+ \(ƯCLN\left(10^{4i};2023\right)=1\)
\(\Rightarrow2024...2024\) (\(j-i\) bộ số \(2024\)) chia hết cho \(2023\) \(\left(đpcm\right)\).