Cho biểu thức
M=căn x +1/2
A)Tìm các giá trị nguyên của x để M nhận giá trị nguyên
B)Tìm giá trị lớn nhất của biểu thức M
c)Tìm các giá trị nguyên của x để A nhận giá trị nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

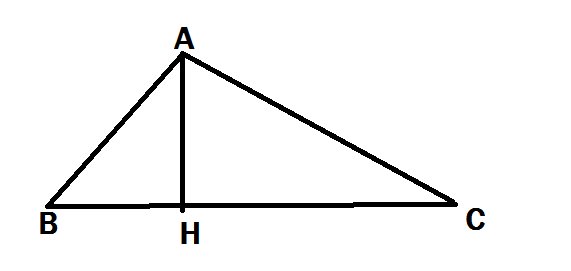
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{9}=\dfrac{1}{AB^2}+\dfrac{1}{25}\)
\(\Leftrightarrow\dfrac{1}{AB^2}=\dfrac{16}{225}\)
\(\Leftrightarrow AB=\dfrac{15}{4}\)
- \(AH.BC=AB.AC\)
\(3.BC=\dfrac{15}{4}.5\)
\(BC=6,25\)
- \(CH=\dfrac{AC^2}{BC}=4\)
=> BH = 6,25 - 4 = 2,25

a) \(\left\{{}\begin{matrix}2x+3y=5\\4x-5y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x+6y=10\\4x-5y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+3y=5\\11y=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+3\cdot\dfrac{9}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+\dfrac{27}{11}=5\\y=\dfrac{9}{11}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=\dfrac{28}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14}{11}\\y=\dfrac{9}{11}\end{matrix}\right.\)
Vậy: \(x=\dfrac{14}{11};y=\dfrac{9}{11}\)

A C B H E F J I O
O là giao của AH và EF
\(AF\perp AB;HE\perp AB\) => AF//HE
\(AE\perp AC;HF\perp AC\) => AE//HF
=> AEHF là hình bình hành mà \(\widehat{A}=90^o\) => AEHF là HCN
\(\Rightarrow AH=EF\) (trong HCN hai đường chéo băng nhau)
\(OA=OH;OE=OF\) (trong hbh hai đường chéo cắt nhau tại trung điểm mỗi đường)
=> OE=OH => tg OEH cân tại O
Vì AEHF là HCN nên
\(\widehat{EAF}=\widehat{EHF}=90^o\) => A và H cùng nhìn EF dưới 1 góc vuông => AEHF là tứ giác nội tiếp đường tròn tâm O bán kính EF
Xét tg vuông BEH có
IB=IH (gt) \(\Rightarrow IE=IB=IH=\dfrac{BH}{2}\) (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền)
=> tg IEH cân tại I \(\Rightarrow\widehat{IEH}=\widehat{IHE}\) (1)
tg OEH cân tại O (cmt) \(\Rightarrow\widehat{OEH}=\widehat{OHE}\) (2)
Mà \(\widehat{IHE}+\widehat{OHE}=\widehat{AHB}=90^o\) (3)
Từ (1) (2) (3) \(\Rightarrow\widehat{IEH}+\widehat{OEH}=\widehat{FEI}=90^o\)
\(\Rightarrow IE\perp EF\) mà EF là đường kính (O) => IE là tiếp tuyến đường tròn (O).
C/m tương tự ta cũng có \(JF\perp EF\) => JF cũng là tiếp tuyến với (O)
=> IE//JF (cùng vuông góc với EF)

\(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)
\(x=36\Rightarrow P=\dfrac{\sqrt{36}+1}{\sqrt{36}-2}=\dfrac{6+1}{6-2}=\dfrac{7}{4}\)
\(x=6-2\sqrt{5}=\sqrt{5^2}-2\sqrt{5}+1=\left(\sqrt{5}-1\right)^2\)
\(\Rightarrow P=\dfrac{\sqrt{\left(\sqrt{5}-1\right)^2}+1}{\sqrt{\left(\sqrt{5}-1\right)^2}-2}=\dfrac{\left|\sqrt{5}-1\right|+1}{\left|\sqrt{5}-1\right|-2}=\dfrac{\sqrt{5}}{\sqrt{5}-3}\)
\(x=\dfrac{2}{2+\sqrt{3}}=\dfrac{4}{4+2\sqrt{3}}\) \(\Rightarrow P=\dfrac{\dfrac{\sqrt{4}}{\sqrt{4+2\sqrt{3}}}+1}{\dfrac{\sqrt{4}}{\sqrt{4+2\sqrt{3}}}-2}=\dfrac{\dfrac{2}{\sqrt{\left(\sqrt{3}+1\right)^2}}+1}{\dfrac{2}{\sqrt{\left(\sqrt{3}+1\right)^2}}-2}=\dfrac{2+\sqrt{3}+1}{\sqrt{3}+1}:\dfrac{2-2\left(\sqrt{3}+1\right)}{\sqrt{3}+1}=\dfrac{2+\sqrt{3}+1}{2-2\sqrt{3}-2}\)
\(x=\dfrac{2-\sqrt{3}}{2}=\dfrac{4-2\sqrt{3}}{4}=\dfrac{\left(\sqrt{3}-1\right)^2}{4}\)
\(\Rightarrow P=\dfrac{\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{2}+1}{\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{2}-2}=\dfrac{\sqrt{3}-1+2}{2}:\dfrac{\sqrt{3}-1-4}{2}=\dfrac{\sqrt{3}+1}{\sqrt{3}-5}\)

\(x-y=2\Rightarrow y=x-2\). Thay vào pt đầu tiên, ta có:
\(\left(m-1\right)x+2\left(x-2\right)=m+1\)
\(\Leftrightarrow\left(m+1\right)x=m+5\)
Ta thấy \(m\) không thể bằng -1 được vì khi đó \(m+5=0\Leftrightarrow m=-5\), trong khi \(m\) không thể mang 2 giá trị cùng một lúc. Vì vậy, \(m\ne-1\). \(\Rightarrow x=\dfrac{m+5}{m+1}\)
\(\Rightarrow y=x-2=\dfrac{m+5}{m+1}-2\) \(=\dfrac{3-m}{m+1}\).
Từ đó, ta có \(xy=\dfrac{\left(m+5\right)\left(3-m\right)}{\left(m+1\right)^2}\).
Rõ ràng \(\left(m+1\right)^2>0\) nên để \(xy>0\) thì \(\left(m+5\right)\left(3-m\right)>0\) \(\Leftrightarrow-5< m< 3\)
Kết luận: Để hpt đã cho có nghiệm duy nhất \(x,y\) thỏa mãn ycbt thì\(-5< m< 3\) và \(m\ne-1\)

a) ĐKXĐ : \(x\sqrt{x}-1\ge0\Leftrightarrow x\ge1\)
b) \(B=\left(\dfrac{2x+1}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right).\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)\)
\(=\dfrac{2x+1-\sqrt{x}.\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right).\left(x+\sqrt{x}+1\right)}.\left(x-2\sqrt{x}+1\right)\)
\(=\dfrac{1}{\sqrt{x}-1}.\left(\sqrt{x}-1\right)^2=\sqrt{x}-1\)
c) Có : \(x=\dfrac{2-\sqrt{3}}{2}=\dfrac{4-2\sqrt{3}}{4}=\dfrac{\left(\sqrt{3}-1\right)^2}{4}\)
Khi đó B = \(\dfrac{\sqrt{3}-1}{2}-1=\dfrac{\sqrt{3}-3}{2}\)
\(a,\) B có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
\(b,B=\left(\dfrac{2x+1}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)\)
\(=\dfrac{2x+1-\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{1+x\sqrt{x}-\sqrt{x}\left(1+\sqrt{x}\right)}{1+\sqrt{x}}\)
\(=\dfrac{2x+1-x+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{1+x\sqrt{x}-\sqrt{x}-x}{1+\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(x-1\right)-\left(x-1\right)}{1+\sqrt{x}}\)
\(=\dfrac{\left(x-1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\sqrt{x}-1\)
\(c,x=\dfrac{2-\sqrt{3}}{2}\Rightarrow B=\sqrt{\dfrac{2-\sqrt{3}}{2}}-1\)
\(=\dfrac{\sqrt{2}.\sqrt{2-\sqrt{3}}}{\sqrt{2}.\sqrt{2}}-\sqrt{2}\) (Nhân \(\sqrt{2}\) để khử căn dưới mẫu)
\(=\dfrac{\sqrt{4-2\sqrt{3}}-2\sqrt{2}}{2}\)
\(=\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}-2\sqrt{2}}{2}\)
\(=\dfrac{\left|\sqrt{3}-1\right|-2\sqrt{2}}{2}\)
\(=\dfrac{\sqrt{3}-1-2\sqrt{2}}{2}\)