Nhân dịp nghỉ lễ 30 tháng 4 các bạn học sinh hai lớp 6A và 6B mỗi một số bánh để liên hoan mỗi hộp có số chiếc bánh như nhau và có nhiều hơn 2 chiếc bánh. Tính ra lớp 6A mua 40 chiếc bánh, lớp 6B mua 28 chiếc bánh. Hỏi mỗi hộp bánh có bao nhiêu chiếc bánh?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left[\left(4-x\right)\cdot3+51\right]:3-2^2=14\)
=>\(\left(4-x+17\right)-4=14\)
=>21-4-x=14
=>17-x=14
=>x=3

Sau ngày thứ nhất số trang sách còn lại chiếm:
\(1-\dfrac{1}{3}=\dfrac{2}{3}\)(quyển sách)
Sau ngày thứ hai thì số trang sách còn lại chiếm:
\(\dfrac{2}{3}\left(1-\dfrac{5}{8}\right)=\dfrac{2}{3}\cdot\dfrac{3}{8}=\dfrac{1}{4}\)(tổng số trang)
Số trang sách của quyển sách đó là:
\(90:\dfrac{1}{4}=360\left(trang\right)\)

\(\dfrac{x-1}{12}+\dfrac{x-1}{20}+\dfrac{x-1}{30}+\dfrac{x-1}{42}+\dfrac{x-1}{56}+\dfrac{x-1}{72}=\dfrac{16}{9}\)
=>\(\left(x-1\right)\left(\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}\right)=\dfrac{16}{9}\)
=>\(\left(x-1\right)\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{8}-\dfrac{1}{9}\right)=\dfrac{16}{9}\)
=>\(\left(x-1\right)\left(\dfrac{1}{3}-\dfrac{1}{9}\right)=\dfrac{16}{9}\)
=>\(\left(x-1\right)\cdot\dfrac{2}{9}=\dfrac{16}{9}\)
=>x-1=8
=>x=9

có 2021 điểm phân biệt thẳng hàng=> sẽ có 2 điểm nằm trên 2 đầu khác nhau
=> Số điểm nằm giữa hai điểm khác là 2021-2 = 2019 điểm

Đề yêu cầu một phép trừ hai số tự nhiên, Thử lần lượt:
49 - 0 = 49 (Số tự nhiên)
49 - 44 = 5 (Số tự nhiên)
49 - 53 = -4 ( Số nguyên âm)
49 - 49 = 0 (Số tự nhiên)
-> Chọn đáp án 53.
Đề yêu cầu một phép trừ hai số tự nhiên. Thử lần lượt: 49 - 0 = 49 là số tự nhiên 49 - 44 = 5 là số tự nhiên 49 - 53 = - 4 là số nguyên âm 49 - 49 = 0 là số tự nhiên Chọn đáp án 53 mình viết hơi bị lệch nên bạn thông cảm cho mình nha
Năm anh em trên một chiếc xe tăng 10 giờ 44 phút ngày 28 tháng 8 năm 2024

Gọi d=ƯCLN(n-5;3n-14)
=>\(\left\{{}\begin{matrix}n-5⋮d\\3n-14⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3n-15⋮d\\3n-14⋮d\end{matrix}\right.\)
=>\(3n-15-3n+14⋮d\)
=>\(-1⋮d\)
=>d=1
=>ƯCLN(n-5;3n-14)=1
=>\(\dfrac{n-5}{3n-14}\) luôn là phân số tối giản
gọi ƯCLN (n-5;3n-14)=d
Ta có (n-5)-(3n-14)\(⋮\)d
<=> (3n-15)-(3n-14)\(⋮\)d
<=> 1\(⋮\)d
=> d=1
=> ƯCLN (n-5;3n-14)=1
Vậy \(\dfrac{n-5}{3n-14}\) là phân số tối giản

Bà Lan lãi số tiền là :
400 000 000 :100x5=20 000 000 (đồng)
Sau 1 năm , bà nhận được là :
400 000 000 +20 000 000 = 420 000 000 đồng
Câu này ngày 19/4 mik vừa trả lời song
https://olm.vn/cau-hoi/ba-lan-gui-tiet-kiem-400-trieu-viet-nam-dong-trong-mot-nam-voi-lai-suat-5-mot-nam-tuc-la-sau-mot-nam-ba-da-nhan-duoc-so-tien-bang-5-so-tien-ba-lan.8957653682187

a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+2=6
=>AB=4(cm)
b: Vì OA<AB
nên A không là trung điểm của OB
c: I là trung điểm của AB
=>\(IA=IB=\dfrac{AB}{2}=2\left(cm\right)\)
Vì AO và AI là hai tia đối nhau
nên A nằm giữa I và O
=>OI=OA+IA=2+2=4(cm)
=>OI=AB(=4cm)
d: Đỉnh: O
Cạnh: OI;OK
a: Trên tia Ox, ta có: OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB+2=6
=>AB=4(cm)
b: Vì OA<AB
nên A không là trung điểm của OB
c: I là trung điểm của AB
=>𝐼𝐴=𝐼𝐵=𝐴𝐵2=2(𝑐𝑚)IA=IB=2AB=2(cm)
Vì AO và AI là hai tia đối nhau
nên A nằm giữa I và O
=>OI=OA+IA=2+2=4(cm)
=>OI=AB(=4cm)
d: Đỉnh: O
Cạnh: OI;OK
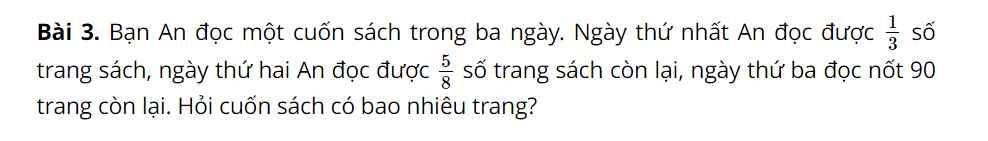
Gọi số bánh trong mỗi hộp là x(cái)
(Điều kiện: \(x\in Z^+\))
\(40=2^3\cdot5;28=2^2\cdot7\)
=>\(ƯCLN\left(40;28\right)=2^2=4\)
Vì số bánh trong mỗi hộp là như nhau
nên \(x\inƯC\left(40;28\right)\)
=>\(x\inƯ\left(4\right)\)
mà x>2
nên x=4(nhận)
Vậy: Mỗi hộp có 4 chiếc bánh