Cho ![]() ABC có a=90 độ,b=60 độ, BE là tia phân giác của b. Trên tia đối của tia AE lấy điểm D sao cho AD = AE. Biết EB = EC.
ABC có a=90 độ,b=60 độ, BE là tia phân giác của b. Trên tia đối của tia AE lấy điểm D sao cho AD = AE. Biết EB = EC.
a) Chứng minh ![]() ABD =
ABD = ![]() ABE và
ABE và ![]() BDE đều.
BDE đều.
b) Chứng minh BD vuông góc BC.
c) Kẻ EK vuông góc BC tại K. Chứng minh: KB = KC.
d) Gọi F là giao điểm của EK và BA. Chứng minh: BE vuông góc CF.



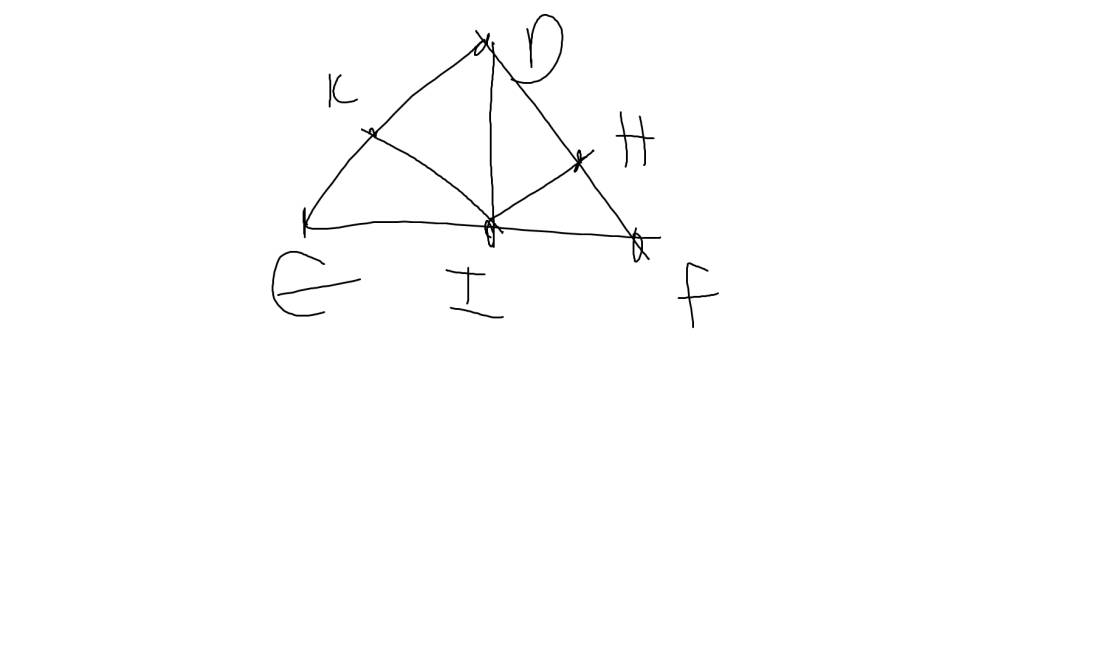
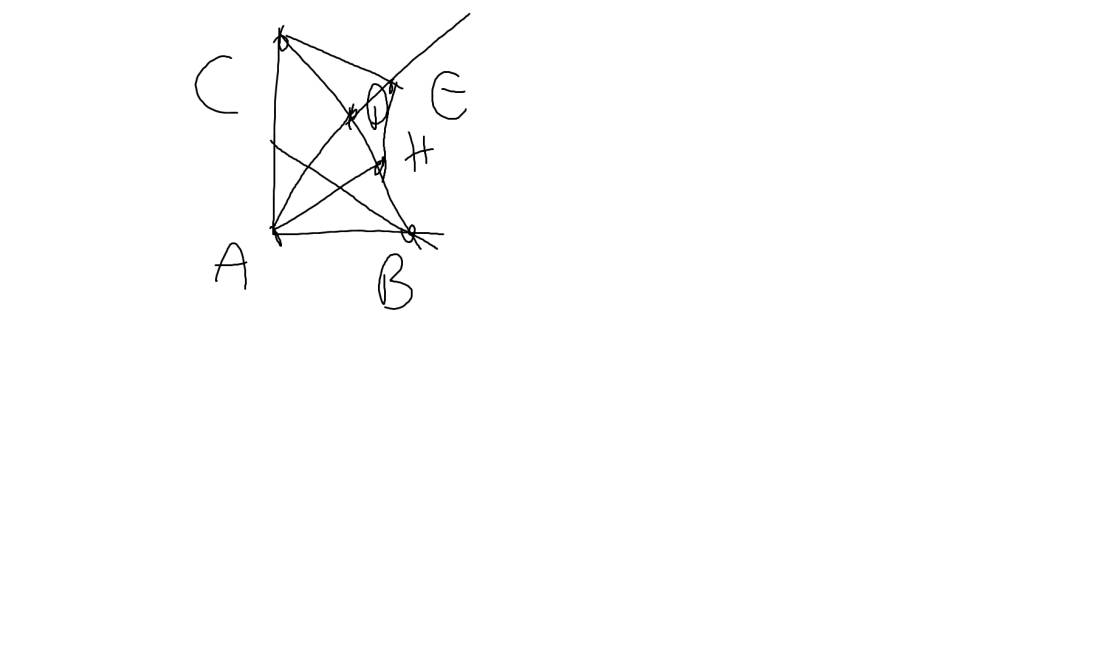

a: Xét ΔABD vuông tại A và ΔABE vuông tại A có
AB chung
AD=AE
Do đó: ΔABD=ΔABE
=>BD=BE
BE là phân giác của góc ABC
=>\(\widehat{ABE}=\widehat{CBE}=\dfrac{\widehat{ABC}}{2}=30^0\)
ΔAEB vuông tại A
=>\(\widehat{AEB}+\widehat{ABE}=90^0\)
=>\(\widehat{AEB}+30^0=90^0\)
=>\(\widehat{AEB}=60^0\)
Xét ΔBDE có BD=BE và \(\widehat{BED}=60^0\)
nên ΔBDE đều
b: ΔBAE=ΔBAD
=>\(\widehat{EBA}=\widehat{DBA}=30^0\)
\(\widehat{DBC}=\widehat{DBA}+\widehat{ABC}=30^0+60^0=90^0\)
=>BD\(\perp\)BC
c: ΔEBC cân tại E
mà EK là đường cao
nên K là trung điểm của BC
=>KB=KC
d: Xét ΔBFC có
FK,CA là các đường cao
FK cắt CA tại E
Do đó: E là trực tâm của ΔBFC
=>BE\(\perp\)CF