\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< 1\)

Đặt \(S=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)

Ta có:

\(S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)

\(S=1-\dfrac{1}{100}\)

\(S=\dfrac{99}{100}\)

mà 

\(\dfrac{1}{2^2}=\dfrac{1}{1.2}\)

\(\dfrac{1}{3^2}< \dfrac{1}{3.2}\)

\(\dfrac{1}{4^2}< \dfrac{1}{3.4}\)

...

\(\dfrac{1}{100^2}< \dfrac{1}{99.100}\)

\(\Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)

\(\Rightarrow A< S\)

\(=>A=\dfrac{99}{100}\)

\(=>A< 1\left(đpcm\right)\)

           Câu 1:

\(\dfrac{6}{-15}\) = \(\dfrac{6:3}{-15:3}\) = \(\dfrac{2}{-5}\); 

\(\dfrac{-4}{-12}\) = \(\dfrac{-4:-4}{12:-4}\) = \(\dfrac{1}{3}\) > \(\dfrac{2}{-5}\)

 \(\dfrac{-14}{35}\) = \(\dfrac{-14:-7}{35:-7}\) = \(\dfrac{2}{-5}\)

 - 0,4 = \(\dfrac{2}{-5}\) 

\(\dfrac{17}{40}\)> \(\dfrac{16}{40}\) ⇒ \(\dfrac{-17}{40}\) < \(\dfrac{-16}{40}\) (Vì khi nhân cả hai vế bất đẳng thức với một số âm thì dấu của bất đẳng thức đổi chiều)

⇒ \(\dfrac{-17}{40}\) < \(\dfrac{-16}{40}\) = \(\dfrac{-16:\left(-8\right)}{40:\left(-8\right)}\) = \(\dfrac{2}{-5}\)

40% = \(\dfrac{40}{100}\) = \(\dfrac{2}{5}\) > \(\dfrac{2}{-5}\)

Từ những lập luận trên ta có trong các phân số đã cho phân số biểu diễn cho số hữu tỉ \(\dfrac{2}{-5}\) lần lượt là các phân số sau:

     \(\dfrac{6}{-15}\); \(\dfrac{-14}{35}\); -0,4

Bài 2:

a; Sắp xếp các phân số sau theo thứ tự tăng dần:

                3,25; 3\(\dfrac{4}{5}\); \(\dfrac{-5}{2}\); 140%; -2

               \(\dfrac{5}{2}\)   > \(\dfrac{4}{2}\)  (hai phân số dương, hai phân số có cùng mẫu số phân số nào có tử số lớn hơn thì phân số đó lớn hơn. 

            ⇒   \(\dfrac{5\times-1}{2}\) < \(\dfrac{4\times-1}{2}\)  (vì khi nhân hai vế với cùng một số âm thì dấu của bất đẳng thức đổi chiều)

          ⇒ \(\dfrac{-5}{2}\) < \(\dfrac{-4}{2}\) = - 2 < 0 (phân số âm luôn nhỏ hơn 0)

3\(\dfrac{4}{5}\) = 3,8;  140% = 1,4 vì  3,8 > 3,25 > 1,4 > 0 

⇒ \(3\dfrac{4}{5}\) > 3,25 > 140% > 0 

Từ những lập luận trên ta có:

 \(\dfrac{-5}{2}\) < -2 < 0 <  140% < 3,25 < 3\(\dfrac{4}{5}\)

Vậy các phân số đã cho được sắp xếp theo thứ tự tăn dần lần lượt là:

     \(\dfrac{-5}{2}\); -2; 140%; 3,25; 3\(\dfrac{4}{5}\)

Lời giải:

$(\frac{2023a}{2024c})^3=(\frac{2024b}{2025a})^3=(\frac{2025c}{2023b})^3=\frac{2023a}{2024b}.\frac{2024b}{2025a}.\frac{2025c}{2023b}=1$

$\Rightarrow \frac{2023a}{2024c}=\frac{2024b}{2025a}=\frac{2025c}{2023b}=1$

$\Rightarrow 2023a=2024c; 2024b=2025a; 2025c=2023b$

Do đó:

$\frac{2023a}{506c}+\frac{2024b}{675a}+\frac{2025c}{289b}=\frac{2024c}{506c}+\frac{2025a}{675a}+\frac{2023b}{289b}$

$=4+3+7=14$

Giải:

Tất cả các số thuộc tập L đều có tính chất chia cho 5 dư 1

Vì 1997 : 5  dư 2 

Vậy 1997 \(\notin\) L

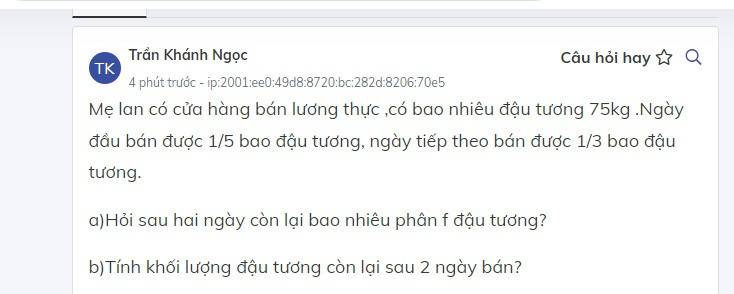
Nếu là có bao đậu tương nặng 75 kg thì làm như sau:

                       Giải:

a; Phân số chỉ số đậu tương còn lại sau hai ngày bán là:

             1 - \(\dfrac{1}{5}\) - \(\dfrac{1}{3}\) = \(\dfrac{7}{15}\) (đậu tương)

b; Sau hai ngày số đậu tương còn lại là:

                75 x  \(\dfrac{7}{15}\) = 35 (kg)

Kết luận: a; Sau hai ngày còn \(\dfrac{7}{15}\) đậu tương.

               b; sau hai ngày bán còn lại 35 kg đậu tương.

Sao lại có bao nhiêu đậu tương 75 kg thế em?

\(\dfrac{3}{-2}\) < 0 (phân số âm luôn nhỏ hơn 0)

 \(\dfrac{4}{9}\) < \(\dfrac{4}{5}\) ( hai phân số dương, hai phân số có cùng tử số phân số nào có mẫu lớn hơn thì phân số đó nhỏ hơn)

0 < \(\dfrac{4}{9}\) (phân số dương luôn lớn hơn 0)

Từ những lập luận trên ta có:

\(\dfrac{3}{-2}< 0< \dfrac{4}{9}< \dfrac{4}{5}\)

Kết luận các phân số đã cho được sắp xếp theo thứ tự tăng dần là:

\(\dfrac{3}{-2}\); 0; \(\dfrac{4}{9}\); \(\dfrac{4}{5}\)

Chọn C. \(\dfrac{3}{-2}\); 0; \(\dfrac{4}{9}\); \(\dfrac{4}{5}\)

9/(7.10) + 9/(10.13) + 9/(13.16) + ... + 9/(58.61)

= 3.(1/7 - 1/10 + 1/10 - 1/13 + 1/13 - 1/16 + ... + 1/58 - 1/61)

= 3.(1/7 - 1/61)

= 3 . 54/427

= 162/427

    \(\dfrac{9}{7.10}\) + \(\dfrac{9}{10.13}\) + \(\dfrac{9}{13.16}\) + ... + \(\dfrac{9}{58.61}\)

=  3.(\(\dfrac{3}{7.10}\) + \(\dfrac{3}{10.13}\) + \(\dfrac{3}{13.16}\) + ... + \(\dfrac{3}{58.61}\))

= 3.(\(\dfrac{1}{7}\) - \(\dfrac{1}{10}\) + \(\dfrac{1}{10}\) - \(\dfrac{1}{13}\) + \(\dfrac{1}{13}\) - \(\dfrac{1}{16}\) + ... +  - \(\dfrac{1}{61}\))

= 3.(\(\dfrac{1}{7}\) - \(\dfrac{1}{61}\))

= 3.\(\dfrac{54}{427}\)

= \(\dfrac{162}{427}\)