Do a³ có số ước là 40 nên a³ = p³.q⁶ hoặc a³ = p⁶.q³

a² = p².q⁵ hoặc a² = p⁵.q²

Số ước của a² là:

(2 + 1).(5 + 1) = 18 (ước)

                                       Giải:

      Tổng số tuổi của hai mẹ con hiện nay là: 46 + 2 x 2 = 50 (tuổi)

                            Theo bài ra ta có sơ đồ:

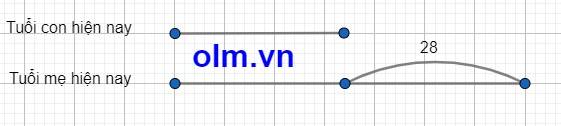
        Theo sơ đồ ta có:

       Tuổi con hiện nay là: (50 - 28) : 2 = 11 (tuổi)

        Tuổi mẹ hiện nay là: 11 + 28 = 39 (tuổi)

       Đáp số:... 

Cách đây $2$ năm trước mẹ hơn con $28$ tuổi, thì hiện nay mẹ vẫn hơn con $28$ tuổi.

- Tuổi mẹ hiện nay:

         $(46+28)÷2=37$ (tuổi)

- Tuổi con hiện nay:

         $37-28=9$ (tuổi)

                  Đáp số: - Mẹ: $37$ tuổi

                               - Con: $9$ tuổi

Gọi a (tờ), b (tờ), c (tờ) lần lượt là số tờ tiền polime ứng với loại 20000 đồng, 50000 đồng và 100000 đồng (a, b, c ∈ ℕ*)

Do tổng số tờ tiền là 24 tờ nên ta có:

a + b + c = 24

Do trị giá của mỗi loại tiền là như nhau nên:

20000a = 50000b = 100000c

2a = 5b = 10c

⇒ a/(1/2) = b/(1/5) = c/(1/10)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

a/(1/2) = b/(1/5) = c/(1/10) = (a + b + c)/(1/2 + 1/5 + 1/10) = 24/(4/5) = 30

2a = 30 ⇒ a = 30 : 2 = 15 (nhận)

5b = 30 ⇒ b = 30 : 5 = 6 (nhận)

10c = 30 ⇒ c = 30 : 10 = 3 (nhận)

Vậy số tờ tiền ứng với loại 20000 đồng; 50000 đồng; 10000 đồng lần lượt là: 15 tờ, 6 tờ; 3 tờ

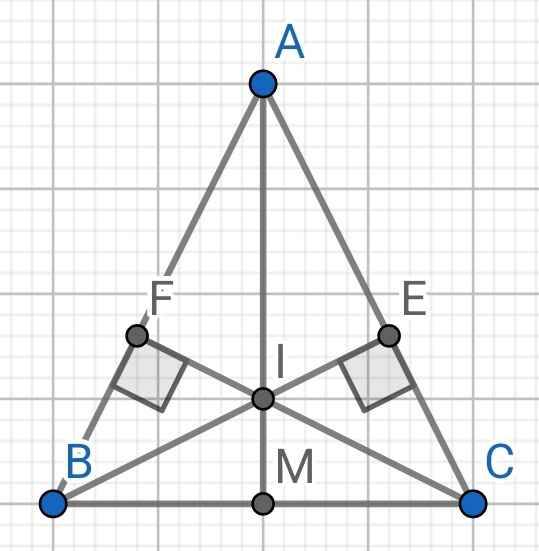
Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆ABE và ∆ACF có:

AB = AC (cmt)

∠A chung

⇒ ∆ABE = ∆ACF (cạnh huyền - góc nhọn)

b) Do ∆ABE = ∆ACF (cmt)

⇒ AE = AF (hai cạnh tương ứng)

Ta có:

BF = AB - AF

CE = AC - AE

Mà AB = AC (cmt)

AF = AE (cmt)

⇒ BF = CE

Do ∆ABE = ∆ACF (cmt)

⇒ ∠ABE = ∠ACF (hai góc tương ứng)

⇒ ∠FBI = ∠ECI

Xét hai tam giác vuông: ∆FBI và ∆ECI có:

BF = CE (cmt)

∠FBI = ∠ECI (cmt)

⇒ ∆FBI = ∆ECI (cạnh góc vuông - góc nhọn kề)

⇒ BI = IC (hai cạnh tương ứng)

⇒ ∆BIC cân tại I

c) ∆FBI vuông tại F

⇒ BI là cạnh huyền nên là cạnh lớn nhất

⇒ BI > FI

Mà BI = IC (cmt)

⇒ IC > FI

d) Do ∆ABC cân tại A (gt)

M là trung điểm của BC (gt)

⇒ AM là đường trung tuyến của ∆ABC

⇒ AM cũng là đường cao của ∆ABC

Mà I là giao điểm của hai đường cao BE và CF

⇒ A, I, M thẳng hàng

12/11 nha

108/11

B=2006^2024
B= ....6
=> B chia 5 dư 1
Có 2006 đồng dư với -1 (mod 223)
=> 2006^2024 đồng dư với (-1)^2024 = 1 (mod 223)
=> B chia 223 dư 1

Là 1 bạn nhé! Nếu cần câu trả lời cụ thể thì tinh tinh cho mình.

498 nhà bạn nhé!

Cám ơn bạn!

   Chúc bạn học tốt! ☺

Lời giải:
Để $A$ là phân số thì $2n-4\neq 0$

$\Leftrightarrow n\neq 2$

Với $n$ nguyên, để $A$ nguyên thì:

$2n+2\vdots 2n-4$
$\Rightarrow (2n-4)+6\vdots 2n-4$

$\Rightarrow 6\vdots 2n-4$

$\Rightarrow 3\vdots n-2$

$\Rightarrow n-2\in\left\{1; -1; 3; -3\right\}$

$\Rightarrow n\in \left\{3; 1; 5; -1\right\}$