Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm M sao cho BA=BM. Kẻ BE vuông góc với AM (E thuộc AM).
a) chứng minh tam giác ABE = tam giác MBE .
b) Gọi N là giao điểm của BE và AC. Chứng minh AN = MN.
c) Kẻ đường cao AH của tam giác ABC. Gọi G là giao điểm của AH với BN. Chứng minh: Góc MGN = góc ANG


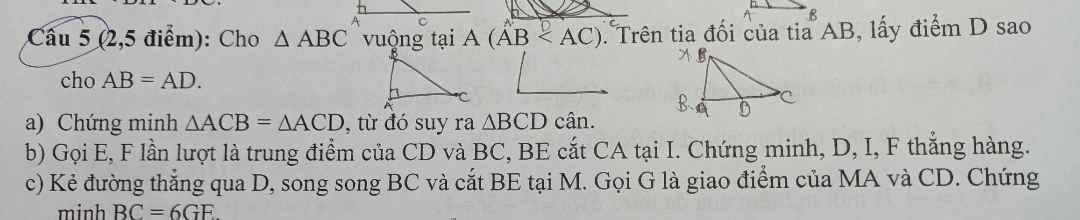



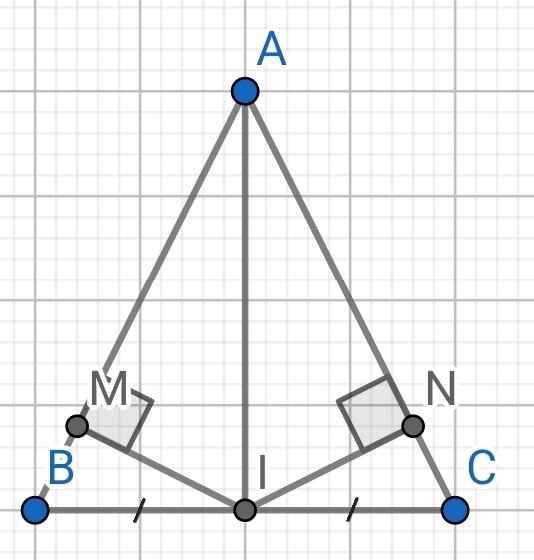
a) Xét hai tam giác vuông: ∆ABE và ∆MBE có:
BA = BM (gt)
BE là cạnh chung
⇒ ∆ABE = ∆MBE (cạnh huyền - cạnh góc vuông)
b) Do ∆ABE = ∆MBE (cmt)
⇒ ∠ABE = ∠MBE (hai góc tương ứng)
⇒ ∠ABN = ∠MBN
Xét ∆ABN và ∆MBN có:
BA = BM (gt)
∠ABN = ∠MBN (cmt)
BN là cạnh chung
⇒ ∆ABN = ∆MBN (c-g-c)
⇒ AN = MN (hai cạnh tương ứng)
c) Do ∆ABN = ∆MBN (cmt)
⇒ ∠BAN = ∠BMN (hai góc tương ứng)
Mà ∠BAN = ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ∠BMN = 90⁰
⇒ MN ⊥ BM
⇒ MN ⊥ BC
Lại có AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Mà MN ⊥ BC (cmt)
⇒ AH // MN
⇒ ∠MGN = ∠ANG (so le trong)
Cho tam giác ABC vuông tại A ( AB < AC ). Trên tia đối của tia AB, lấy điểm D sao cho AB = AD
a) Chứng minh tam giác ACB = tam giác ACD từ đó suy ra tam giác BCD cân.
b) Gọi E, F lần lượt là trung điểm của CD và BC, BE cắt CA tại I. Chứng minh, D, I, F thẳng hàng.
c) Kẻ đường thẳng qua D, song song BC và cắt BE tại M. Gọi G là giao điểm của MA và CD. Chứng minh BC = 6GF
Giúp tui câu này nha 🥺