a, \(\dfrac{254\times399-145}{254+399\times253}\)

= \(\dfrac{\left(253+1\right)\times399-`45}{254+399\times253}\)

= \(\dfrac{253\times399+399-145}{253\times399+254}\)

= \(\dfrac{253\times399+254}{253\times399+254}\)

= 1

b, \(\dfrac{5932+6001\times5931}{5932\times6001-69}\)

= \(\dfrac{5932+6001\times5931}{\left(5931+1\right)\times6001-69}\)

= \(\dfrac{5932+6001\times5931}{5931\times6001+6001-69}\)

= \(\dfrac{5932+6001\times5931}{5931\times6001+5932}\)

= 1

a) Số lẻ đầu tiên trong dãy: 101

Số lẻ cuối trong dãy: 999

Số phần tử: \(\dfrac{999-101}{2}+1=450\)

b) Số phần tử \(\dfrac{\left(302-5\right)}{3}+1=100\)

c) Số phần tử: \(\dfrac{279-7}{4}+1=69\)

a) \(A=\left\{101;103;...999\right\}\)

Số phần tử của tập hợp A là :

\(\left(999-101\right):2+1=450\left(phần.tử\right)\)

b) \(B=\left\{5;8;11;...;299;302\right\}\)

Số phần tử của tập hợp B là :

\(\left(302-5\right):3+1=100\left(phần.tử\right)\)

c) \(C=\left\{7;11;15;...;275;279\right\}\)

Số phần tử của tập hợp C là :

\(\left(279-7\right):4+1=69\left(phần.tử\right)\)

Lời giải:
a. $420=2^2.3.5.7$ chia hết cho các số nguyên tố $2,3,5,7$

b. $343=7^3$ chia hết cho số nguyên tố $7$

c. $264=2^3.3.11$ chia hết cho các số nguyên tố $2,3,11$

d. $34=2.17$ chia hết cho các số nguyên tố $2,17$

\(x\) \(\in\) B(11) = {0; 11; 22; 33; 44;...;}

Vì 28 < \(x\) < 38

\(x\)  = 33

E có 26 phần tử

Tập hợp D là tập hợp các số tự nhiên từ 1 đến 51. Tập hợp E là tập hợp con của tập hợp D, bao gồm tất cả các số tự nhiên lẻ từ 1 đến 51.

Do đó, tập hợp E có số phần tử bằng số lượng các số tự nhiên lẻ từ 1 đến 51.

Số lượng các số tự nhiên lẻ từ 1 đến n là n/2, với n là số tự nhiên.

Vì vậy, tập hợp E có 51/2 = 25 phần tử.

Đáp án: 25

Tick cho mình cái

10

x - 5 = 25 : 5 

x - 5 = 5 

        x = 5 + 5 

        x = 10 

đáp án đây bn nhé 

chúc bn hok tốt 

Tổng độ dài đáy lớn và đáy bé của hình thang ABCD là: 

     29,43 x 2: 3,6 =  16,35 (m²)

Gọi độ dài đáy lớn là: \(x\) (m); \(x\) > 0

Thì độ dài đáy bé là: \(x\) - 7,5 (m)

Theo bài ra ta có phương trình:  \(x\) + \(x\) - 7,5 = 16,35 

                                                    2\(x\)              = 16,35 + 7,5

                                                    2\(x\)               = 23,85

                                                       \(x\)               = 23,85:2

                                                       \(x\)               = 11,925 (m)

Dộ dài đáy bé của hình thang ABCD là: 11,925 - 7,5 = 4,425 (m)

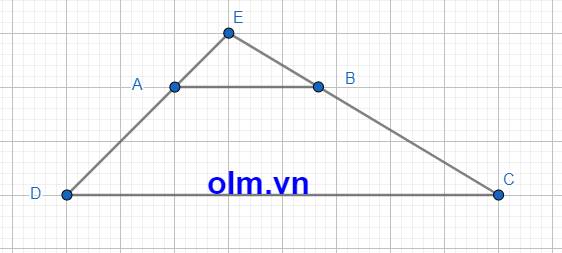
AE = DE - AD = \(\dfrac{3}{2}\)AD - AD = \(\dfrac{1}{2}\)AD
 

⇒S_AEB = \(\dfrac{1}{2}\)S_{ABD (Vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy DE và AE = \(\dfrac{1}{2}\)AD)}

S_ABD = 4,425 x 3,6 : 2 = 7,965 (m²)

S_ABE = 7,965 : 2 = 3,9825 (m²)

Không có phẩy các bạn nhé .

\(5^3+3^3=125+27=152\)

15,652

5\(x\)³ + 29  = 69

5\(x^3\)          = 69 - 29

5\(x^3\)          =  40

  \(x^3\)           = 40:5

   \(x^3\)          = 8

   \(x^3\)          = 2³

   \(x\)           = 2

475 : 25 

= (475 . 4) : (25 . 4)

= 1900 : 100

= 19