ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne9\end{matrix}\right.\)

\(B=\left(\dfrac{3}{x+3\sqrt{x}}-\dfrac{1}{\sqrt{x}-3}\right)\cdot\dfrac{x-9}{\sqrt{x}}\)

\(=\left(\dfrac{3}{\sqrt{x}\cdot\left(\sqrt{x}+3\right)}-\dfrac{1}{\sqrt{x}-3}\right)\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}}\)

\(=\dfrac{3\left(\sqrt{x}-3\right)-x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\cdot\left(\sqrt{x}+3\right)\cdot\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\sqrt{x}}\)

\(=\dfrac{3\sqrt{x}-9-x-3\sqrt{x}}{x}=\dfrac{-x-9}{x}\)

\(P=\dfrac{2x+\sqrt{x}}{\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x-\sqrt{x}+1}+1\)

\(=\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1\)

\(=2\sqrt{x}+1-\sqrt{x}-1+1\)

\(=\sqrt{x}+3\)

\(P=\dfrac{2x+\sqrt{x}}{\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x-\sqrt{x}+1}+1\)

\(P=\dfrac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x-\sqrt{x}+1}+1\)

\(P=2\sqrt{x}+1-\sqrt{x}-1+1\)

\(P=\sqrt{x}+1\)

Lời giải:
Áp dụng BĐT Cô-si:

$\frac{x}{4}+\frac{1}{x}\geq 2\sqrt{\frac{x}{4}.\frac{1}{x}}=1$
$\frac{3}{4}x\geq \frac{3}{4}.2=\frac{3}{2}$ do $x\geq 2$

Cộng theo vế 2 BĐT trên thu được:

$A\geq 1+\frac{3}{2}=\frac{5}{2}$
Vậy GTNN của $A$ là $\frac{5}{2}$. Giá trị này đạt được tại $x=2$

Câu 2:

1; Giải hệ phương trình:

\(\left\{{}\begin{matrix}x+y=7\\3x-2y=16\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=7-y\\3x=16+2y\end{matrix}\right.\)

 \(\left\{{}\begin{matrix}x=7-y\\3.\left(7-y\right)=16+2y\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=7-y\\21-3y=16+2y\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=7-y\\2y+3y=21-16\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=7-y\\5y=5\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=7-y\\y=5:5\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=7-y\\y=1\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=7-1\\y=1\end{matrix}\right.\)

\(\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\)

Vậy (\(x;y\)) = (6; 1)

2; Đường thẳng y = (m - 3)\(x\) + 2m -  2 cắt đường thẳng y = 3\(x\) - 2

tại một điểm trên trục hoành nên y = 0

Ta có hệ phương trình: 

\(\left\{{}\begin{matrix}\left(m-3\right)x+2m-2=0\\3x-2=0\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\left(m-3\right)x+2m-2=0\\3x=2\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\left(m-3\right)x+2m-2=0\left(1\right)\\x=\dfrac{2}{3}\end{matrix}\right.\)

Thay \(x\) = \(\dfrac{2}{3}\) vào phương trình (1) ta có:

(m - 3)\(\dfrac{2}{3}\) + 2m - 2= 0

\(\dfrac{2}{3}\)m - 2 + 2m -  2 = 0

  \(\dfrac{2}{3}\)m + 2m = 2 + 2

    \(\dfrac{8}{3}\)m = 4

       m = 4 : \(\dfrac{8}{3}\)

       m = \(\dfrac{3}{2}\) 

Kết luận với m = \(\dfrac{3}{2}\) thì phương trình đường thẳng y = (m - 3)\(x\) + 2m - 2 cắt đường thẳng y = 3\(x\) - 2 tại một điểm trên trục hoành. 

x + 3y = 5

x + y = 3

=>2y = 5 - 3 = 2

=> y = 2 : 2 = 1

=> x = 3 - 1

Bài dưới em không biết, em mới lớp 4 thôi...

Bài 1:

 \(\left\{{}\begin{matrix}x+3y=5\\x+y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x+3y-x-y=5-3\\x+y=3\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2x=2\\y=3-x\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=1\\y=3-1=2\end{matrix}\right.\)

Bài 2:

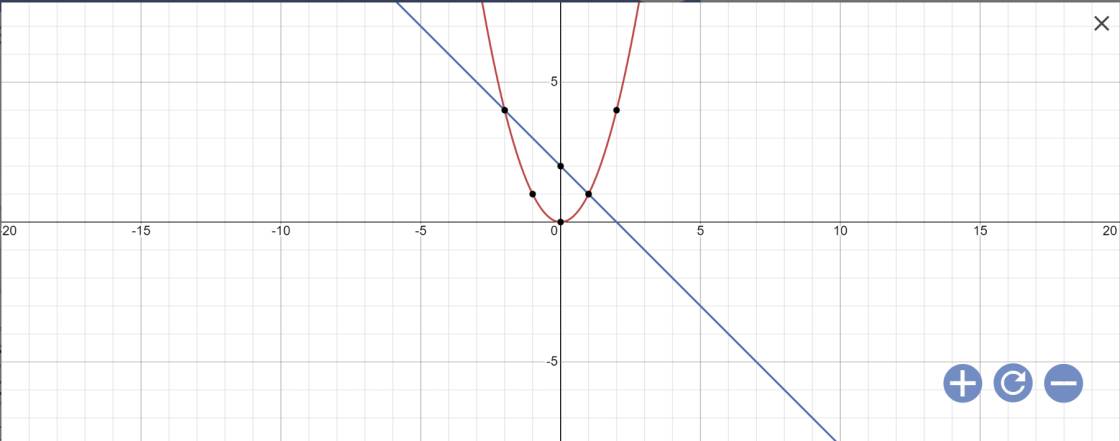
Phương trình hoành độ giao điểm là:

\(x^2=-x+2\)

=>\(x^2+x-2=0\)

=>(x+2)(x-1)=0

=>\(\left[{}\begin{matrix}x=-2\\x=1\end{matrix}\right.\)

Thay x=-2 vào y=-x+2, ta được:

y=-(-2)+2=4

Thay x=1 vào y=-x+2, ta được:

y=-1+2=1

Vậy: (P) giao (d) tại A(-2;4); B(1;1)

a: Xét (O) có

AB,AC lần lượt là các tiếp tuyến

DO đó: AO là phân giác của góc BAC

=>\(\widehat{BAO}=\dfrac{\widehat{BAC}}{2}=30^0\)

Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}\)

=>\(\dfrac{2}{OA}=sin30=\dfrac{1}{2}\)

=>OA=4(cm)

Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên OBAC là tứ giác nội tiếp đường tròn đường kính OA

Tâm là trung điểm của OA

Bán kính là \(R=\dfrac{OA}{2}=2\left(cm\right)\)

b: Xét (O) có

\(\widehat{ABM}\) là góc tạo bởi tiếp tuyến BA và dây cung BM

\(\widehat{BNM}\) là góc nội tiếp chắn cung BM

Do đó: \(\widehat{ABM}=\widehat{BNM}\)

Xét ΔABM và ΔANB có

\(\widehat{ABM}=\widehat{ANB}\)

\(\widehat{BAM}\) chung

Do đó: ΔABM~ΔANB

=>\(\dfrac{AB}{AN}=\dfrac{AM}{AB}\)

=>\(AB^2=AM\cdot AN\)

ĐKXĐ: \(x\ge0;x\ne1\)

\(A=\left(\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}}{x-1}\right):\dfrac{1}{\left(\sqrt{x}+1\right)^2}+1\)

\(=\left(\dfrac{\sqrt{x}+1+2\left(\sqrt{x}-1\right)-3\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right).\left(\sqrt{x}+1\right)^2+1\)

\(=\dfrac{-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\left(\sqrt{x}+1\right)^2+1\)

\(=\dfrac{-\left(\sqrt{x}+1\right)}{\sqrt{x}-1}+1\)

\(=\dfrac{-2}{\sqrt{x}-1}\)

\(A=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{2}{\sqrt{x}+1}-\dfrac{3\sqrt{x}}{x-1}\right):\dfrac{1}{x+2\sqrt{x}+1}+1\)

\(ĐKXĐ:x\ge0.x\ne1\)

\(A=\left(\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{2\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{3\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x+1}\right)}\right):\dfrac{1}{\left(\sqrt{x}+1\right)^2}+1\)

\(A=\left(\dfrac{\sqrt{x}+1+2\sqrt{x}-2-3\sqrt{x}}{x-1}\right):\dfrac{1}{\left(\sqrt{x}+1\right)^2}+1\)

\(A=\dfrac{-1}{x-1}.\dfrac{\left(\sqrt{x}+1\right)^2}{1}+1\)

\(A=\dfrac{-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)^2}{1}+1\)

\(A=\dfrac{-1}{\sqrt{x}-1}.\dfrac{\sqrt{x}+1}{1}+1\)

\(A=\dfrac{-\left(\sqrt{x}+1\right)}{\sqrt{x}-1}+1\)

\(A=\dfrac{-\sqrt{x}-1}{\sqrt{x-1}}+1\)

\(A=\dfrac{-\sqrt{x}-1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x-1}}\)

\(A=\dfrac{-2}{\sqrt{x}-1}\)

a: Xét tứ giác BDOM có \(\widehat{BDO}+\widehat{BMO}=90^0+90^0=180^0\)

nên BDOM là tứ giác nội tiếp

=>\(\widehat{DOM}+\widehat{CBE}=180^0\)

Xét (O) có

\(\widehat{CBE}\) là góc nội tiếp chắn cung CE

\(\widehat{CAE}\) là góc nội tiếp chắn cung CE

Do đó: \(\widehat{CBE}=\widehat{CAE}\)

=>\(\widehat{DOM}+\widehat{CAE}=180^0\)

1: Xét tứ giác ABCK có \(\widehat{BAC}=\widehat{BKC}=90^0\)

nên ABCK là tứ giác nội tiếp

2:

Xét ΔCKB vuông tại K và ΔCEF vuông tại E có

\(\widehat{KCB}\) chung

Do đó: ΔCKB~ΔCEF

=>\(\dfrac{CK}{CE}=\dfrac{CB}{CF}\)

=>\(CK\cdot CF=CB\cdot CE\)

Xét ΔACB vuông tại A có AE là đường cao

nên \(CE\cdot CB=CA^2\)

=>\(CA^2=CK\cdot CF\)

=>\(\dfrac{CA}{CF}=\dfrac{CK}{CA}\)

Xét ΔCAK và ΔCFA có

\(\dfrac{CA}{CF}=\dfrac{CK}{CA}\)

\(\widehat{ACK}\) chung

Do đó: ΔCAK~ΔCFA

1. Chứng minh tứ giác ABCK nội tiếp:
Ta có ∆ABC vuông tại A, do đó góc ACB là góc vuông.
Gọi H là trực tâm của ∆BFC, suy ra BH ⊥ FC.
Vì A là trung điểm của EF, AE = EF và AE ⊥ BC (vì AE là đường cao), suy ra E là trung điểm của BC.
Từ đó, BK cũng là đường cao của ∆BFC, suy ra BK ⊥ FC.
Vậy tứ giác ABCK có hai đường chéo AC và BK cùng vuông góc với cạnh BC, suy ra tứ giác ABCK nội tiếp đường tròn đường kính BC.
2. Chứng minh tam giác CAK đồng dạng với tam giác CFA:
Vì tứ giác ABCK nội tiếp, suy ra góc BAC = góc BKC (cùng chắn cung BC).
Góc BAC là góc vuông (vì ∆ABC vuông tại A), suy ra góc BKC cũng là góc vuông.
Do đó, ∆BKC vuông tại K.
Vì ∆ABC vuông tại A, suy ra góc ABC + góc BAC = 90°.
Tương tự, trong ∆BFC vuông tại F, ta có góc BFC + góc FBC = 90°.
Vì E là trung điểm của BC, suy ra BE = EC và góc ABC = góc FBC.
Từ đó, góc BAC = góc BKC và góc ABC = góc FBC, suy ra ∆CAK đồng dạng với ∆CFA theo trường hợp góc-góc.
3. Chứng minh H là trung điểm của AE:
Vì H là trực tâm của ∆BFC, suy ra BH ⊥ FC và CH ⊥ BF.
Vì BK là đường cao của ∆BFC, suy ra BK ⊥ FC.
Vì E là trung điểm của BC và AE ⊥ BC, suy ra AE là đường trung bình của ∆BFC.
Đường trung bình trong tam giác vuông cũng là đường cao, suy ra H là giao điểm của AE và BK.
Do đó, H chia AE thành hai đoạn bằng nhau, suy ra H là trung điểm của AE.