a) Hệ phương trình có nghiệm duy nhất là 

\(\left\{{}\begin{matrix}2x-y=3\\x+4y=6\end{matrix}\right.\)

b) Hệ phương trình có vô số nghiệm là 

\(\left\{{}\begin{matrix}2x-y=3\\4x-2y=6\end{matrix}\right.\)

em mới lên lớp 7 nên chưa giải đc

e k b lm

\(\dfrac{\sqrt{15}-\sqrt{5}}{\sqrt{3}-1}+\dfrac{5-2\sqrt{5}}{2\sqrt{5}-4}\)

\(=\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}+\dfrac{\sqrt{5}\left(\sqrt{5}-2\right)}{2\left(\sqrt{5}-2\right)}\)

\(=\sqrt{5}+\dfrac{\sqrt{5}}{2}\)

\(=\dfrac{2\sqrt{5}+\sqrt{5}}{2}\)

\(=\dfrac{3\sqrt{5}}{2}\)

A B C D O E F G H x y I

1/

Ta có

sđ cung AC = sđ cung BC (1)

\(sđ\widehat{CFG}=\dfrac{1}{2}\left(sđcungBC+sđcungAE\right)\) (góc có đỉnh ở trong hình tròn) (2)

\(sđ\widehat{CHE}=\dfrac{1}{2}sđcungCAE=\dfrac{1}{2}\left(sđcungAC+sđcungAE\right)\) (góc nội tiếp) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{CFG}=\widehat{CHE}\)

Ta có

\(\widehat{CFG}+\widehat{EFG}=\widehat{EFC}=180^o\)

\(\Rightarrow\widehat{CHE}+\widehat{EFG}=180^o\)

=> EFGH là tứ giác nội tiếp (Tứ giác có hai góc đối bù nhau là tứ giác nội tiếp)

2/

sđ cung AC = sđ cung BC (4)

\(sđ\widehat{AGC}=\dfrac{1}{2}\left(sđcungAC+sđcungBH\right)\) (5) (góc có đỉnh ở trong hình tròn)

\(sđ\widehat{CHy}=\dfrac{1}{2}sđcungCBH=\dfrac{1}{2}\left(sđcungBC+sđcungBH\right)\) (6) (Góc giữa tiếp tuyến và dây cung)

Từ (4) (5) (6) \(\Rightarrow\widehat{AGC}=\widehat{CHy}\)

Mà AC = AG (gt) => tgACG cân tại A \(\Rightarrow\widehat{AGC}=\widehat{ACG}\)

\(\Rightarrow\widehat{ACG}=\widehat{CHy}\) mà 2 góc trên ở vị trí so le trong => xy//AC

ko bt

\(\sqrt[]{3-\sqrt[]{5}}:\sqrt[]{2}\)

\(=\sqrt[]{3-\sqrt[]{5}}.\dfrac{1}{\sqrt[]{2}}\)

\(=\dfrac{\sqrt[]{3-\sqrt[]{5}}}{\sqrt[]{2}}\)

\(=\sqrt[]{\dfrac{3-\sqrt[]{5}}{2}}\)

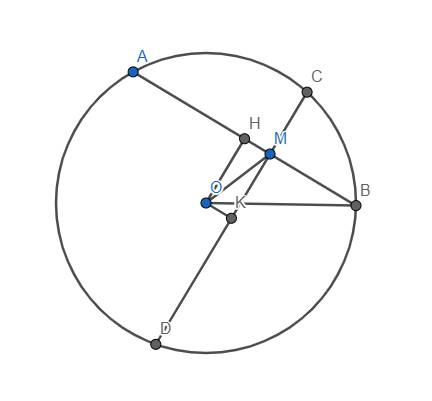
 Hạ \(OH\perp AB\), \(OK\perp CD\). Dễ thấy tứ giác OHMK là hình chữ nhật \(\Rightarrow HK=OM\)

 Lại có \(AB^2=4HB^2=4\left(OB^2-OH^2\right)=4R^2-4OH^2\) (1)

 và \(CD^2=4CK^2=4\left(OC^2-OK^2\right)=4R^2-4OK^2\) (2)

Từ (1) và (2), suy ra \(AB^2+CD^2=8R^2-4\left(OH^2+OK^2\right)\) \(=8R^2-4HK^2=8R^2-4OM^2\) không đổi, đpcm.

A B C H D I K

a/

\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10cm\) (pitago)

\(\dfrac{AD}{DC}=\dfrac{AB}{AC}=\dfrac{6}{8}=\dfrac{3}{4}\) (T/c đường phân giác)

\(\Rightarrow AD=\dfrac{3}{\left(3+4\right)}.AC=\dfrac{30}{7}cm\)

\(DC=\dfrac{4}{3+4}.AC=\dfrac{40}{7}cm\)

\(AB^2=BH.BC\) (Trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)

\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)

\(\Rightarrow CH=BC-BH=10-3,6=6,4cm\)

\(AH^2=BH.CH\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông xuống cạnh huyền bằng tích các hình chiếu của 2 cạnh góc vuông trên cạnh huyền)

\(\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3,6.6,4}=4,8cm\)

b/

Xét tg vuông BHI và tg vuông ABD có

\(\widehat{ABD}=\widehat{CBD}\) (gt)

=> tg BHI đồng dạng với tg ABD \(\Rightarrow\dfrac{BD}{BI}=\dfrac{AB}{BH}\)

Xét tg ABH có

\(\dfrac{AI}{HI}=\dfrac{AB}{BH}\) (t/c đường phân giác )

\(\Rightarrow\dfrac{BD}{BI}=\dfrac{AI}{HI}\Rightarrow AI.BI=BD.HI\)

c/

HK//BD => HK//DI => DIHK là hình thang

Ta có tg BHI đồng dạng với tg ABD (cmt)

\(\Rightarrow\widehat{BIH}=\widehat{ADB}\) (1)

Ta có HK//BD (gt)

\(\Rightarrow\widehat{BIH}=\widehat{IHK}\) (góc so le trong) (2)

\(\Rightarrow\widehat{ADB}=\widehat{DKH}\) (góc đồng vị) (3)

Từ (1) (2) và (3) \(\Rightarrow\widehat{IHK}=\widehat{DKH}\)

=> DIHK là hình thang cân

\(P=\dfrac{2x\sqrt[]{x}-\sqrt[]{x}+1}{x-1}\left(x\ge0;x\ne1\right)\)

\(\Rightarrow P=\dfrac{x\sqrt[]{x}-\sqrt[]{x}+x\sqrt[]{x}+1}{x-1}\)

\(\Rightarrow P=\dfrac{\sqrt[]{x}\left(x-1\right)+\sqrt[]{x^3}+1}{x-1}\)

\(\Rightarrow P=\dfrac{\sqrt[]{x}\left(x-1\right)}{x-1}+\dfrac{\left(\sqrt[]{x}+1\right)\left(x-\sqrt[]{x}+1\right)}{\left(\sqrt[]{x}-1\right)\left(\sqrt[]{x}+1\right)}\)

\(\Rightarrow P=\sqrt[]{x}+\dfrac{\left(x-\sqrt[]{x}+1\right)}{\left(\sqrt[]{x}-1\right)}\)

Áp dụng định lí Py-ta-go vào tam giác vuông ABC, ta có:

\(AC=\sqrt{BC^2-AB^2}=\sqrt{8^2-6^2}=2\sqrt{7}\)                                                                     

Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:       

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{\left(2\sqrt{7}\right)^2}\\ \Rightarrow AH=\dfrac{3\sqrt{7}}{2}\)                           

 Áp dụng hệ thức lượng trong tam giác vuông ABC, ta có:     

\(AB^2=BH\cdot BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{8}=\dfrac{9}{2}\)                               

Ta có: 

\(sin\left(\widehat{ACB}\right)=\dfrac{AB}{BC}=\dfrac{6}{8}=\dfrac{3}{4}\\ \Rightarrow\widehat{ACB}\simeq48^o35'\)