N = x3 + x2.y - 2x2 -xy - y2 + 3y + x-1 biết x+y=2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


7/x = -3/15
⇒ 7⨯15 = x ⨯ (-3)
⇒ 105 = x ⨯ (-3)
⇒ x =105/-3
⇒ x =-35

Đặt \(f\left(x\right)=ax^2+bx+c\)
\(f\left(-2\right)\cdot f\left(3\right)\)
\(=\left[a\cdot\left(-2\right)^2+b\cdot\left(-2\right)+c\right]\left[a\cdot3^2+b\cdot3+c\right]\)
\(=\left(4a-2b+c\right)\left(9a+3b+c\right)\)
\(=\left(13a+b+2c-9a-3b-c\right)\left(9a+3b+c\right)\)
\(=\left(0-9a-3b-c\right)\left(9a+3b+c\right)=-\left(9a+3b+c\right)^2< =0\)

Gọi x, x + 1, x + 2 là ba số tự nhiên liên tiếp cần tìm (x ∈ ℕ)
Tích hai số đầu: x(x + 1) = x² + x
Tích hai số sau: (x + 1)(x + 2) = x² + 2x + x + 2 = x² + 3x + 2
Do tích hai số đầu nhỏ hơn tích hai số sau là 50 đơn vị nên:
x² + 3x + 2 - x² - x = 50
2x = 50 - 2
2x = 48
x = 48 : 2
x = 24 (nhận)
Vậy ba số cần tìm lần lượt là: 24; 25; 26
Gọi 3 số tự nhiên liên tiếp đó lần lượt là
Vì tích 2 số đầu nhỏ hơn tích 2 số sau là 50
Từ nên
Vậy 3 số tự nhiên liên tiếp cần tìm là

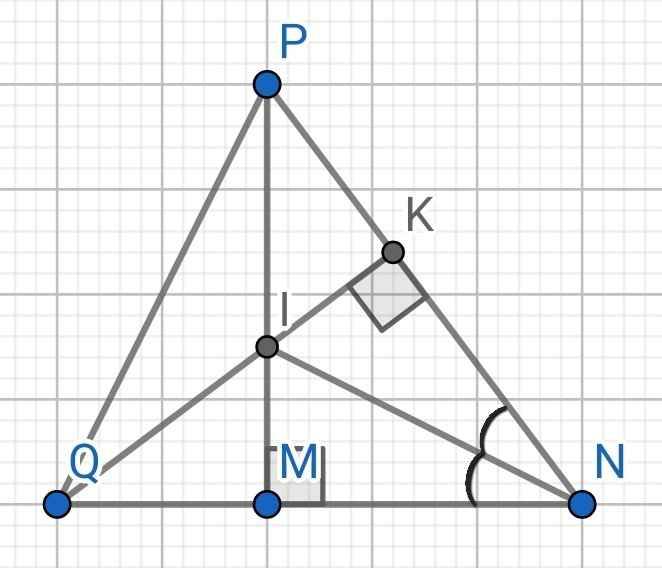
b) Do IK ⊥ NP (gt)
⇒ QK ⊥ NP
⇒ QK là đường cao của ∆NQP
Do ∆MNP vuông tại M (gt)
⇒ PM ⊥ MN
⇒ PM ⊥ QN
⇒ PM là đường cao thứ hai của ∆NQP
Mà PM và QK cắt nhau tại I
⇒ NI là đường cao thứ ba của ∆NQP
Do NI là tia phân giác của ∠MNP (gt)
⇒ NI là tia phân giác của ∠QNP
⇒ NI là đường phân giác của ∆NQP
∆NQP có:
NI là đường cao (cmt)
NI là đường phân giác (cmt)
⇒ ∆NQP cân tại N
\(N=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(=x^2\left(x+y\right)-2x^2-y\left(x+y\right)+3y+x-1\)
\(=2x^2-2x^2-2y+3y+x-1\)
=x+y-1
=2-1
=1