Tháng Một, chị Hạnh mua kg táo với giá đồng. Tháng Hai giá táo cao hơn tháng Một, chị Hạnh mua kg táo với giá đồng. Hỏi tháng Hai giá mỗi ki-lô-gam táo tăng lên bao nhiêu so với tháng Một?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{4}{9}+\dfrac{11}{8}-\dfrac{5}{6}=\dfrac{131}{72}-\dfrac{5}{6}=\dfrac{71}{72}\)

\(\left\{{}\begin{matrix}3x+2y=1\\5x+3y=-4\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\left(3x+2y\right).3=1.3\\\left(5x+3y\right).2=-4.2\end{matrix}\right.\)
\(\left\{{}\begin{matrix}9x+6y=3\\10x+6y=-8\end{matrix}\right.\)
\(\left\{{}\begin{matrix}9x+6y=3\\10x+6y-9x-6y=-8-3\end{matrix}\right.\)
\(\left\{{}\begin{matrix}9x+6y=3\\x=-11\end{matrix}\right.\)
\(\left\{{}\begin{matrix}9.\left(-11\right)+6y=3\\x=-11\end{matrix}\right.\)
\(\left\{{}\begin{matrix}6y=3+99\\x=-11\end{matrix}\right.\)
\(\left\{{}\begin{matrix}6y=102\\x=-11\end{matrix}\right.\)
\(\left\{{}\begin{matrix}y=102:6\\x=-11\end{matrix}\right.\)
\(\left\{{}\begin{matrix}y=17\\x=-11\end{matrix}\right.\)
Vậy (\(x;y\)) = (-11; 17)

Olm chào em, vấn đề em hỏi Olm xin hỗ trợ như sau:
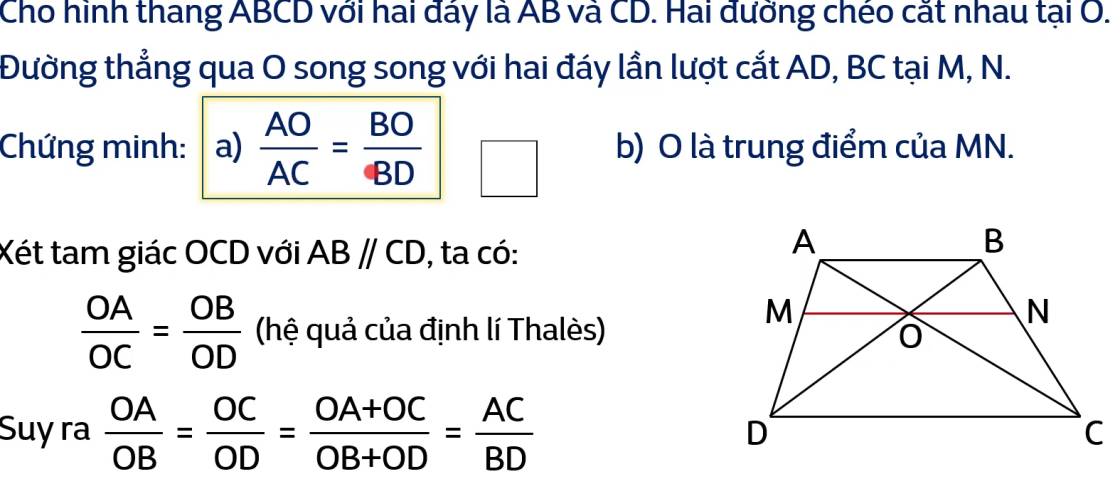
Đoạn \(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả của định lí Thales). Em hiểu rồi đúng chưa.
Từ dòng suy ra \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) = \(\dfrac{AC}{BD}\) là em không hiểu tại sao phải không?
Vậy Olm sẽ giảng cho em như sau:
\(\dfrac{OA}{OC}\) = \(\dfrac{OB}{OD}\) (hệ quả định lí Thales) ⇒ \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) (tc tỉ lệ thức)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{OA+OC}{OB+OD}\) (1)
Mặt khác O là giao điểm của AC và BD nên
\(\left\{{}\begin{matrix}OA+OC=AC\\OB+OD=BD\end{matrix}\right.\) (2)
Thay (2) vào (1) ta có: \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\) = \(\dfrac{AC}{BD}\)
Giải thích đoạn: \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\)
\(\dfrac{OA}{OB}\) = \(\dfrac{AC}{BD}\) (cmt) ⇒\(\dfrac{AO}{BO}=\dfrac{AC}{BD}\) ⇒ \(\dfrac{AO}{AC}\) = \(\dfrac{BO}{BD}\) (tính chất tỉ lệ thức)
Mọi chi tiết bài giảng liên hệ zalo 0385 168 017


\(\left\{{}\begin{matrix}-3x+2y=-11\\x-3y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x+2y=-11\\3x-6y=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4y=-11+18=7\\x-3y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=-\dfrac{7}{4}\\x=3y+6=3\cdot\dfrac{-7}{4}+6=-\dfrac{21}{4}+6=\dfrac{3}{4}\end{matrix}\right.\)

Gọi vận tốc dự định của ô tô là x(km/h)
(Điều kiện: x>0)
Thời gian dự định sẽ đi hết quãng đường là \(\dfrac{80}{x}\left(giờ\right)\)
Thời gian đi hết nửa quãng đường đầu tiên là \(\dfrac{40}{x}\left(giờ\right)\)
Vận tốc đi trên nửa quãng đường còn lại là:
x+10(km/h)
Thời gian đi hết nửa quãng đường còn lại là: \(\dfrac{40}{x+10}\left(giờ\right)\)
8 phút=2/15 giờ
Theo đề, ta có phương trình:
\(\dfrac{40}{x}+\dfrac{40}{x+10}+\dfrac{2}{15}=\dfrac{80}{x}\)
=>\(-\dfrac{40}{x}+\dfrac{40}{x+10}=-\dfrac{2}{15}\)
=>\(\dfrac{40}{x}-\dfrac{40}{x+10}=\dfrac{2}{15}\)
=>\(\dfrac{20}{x}-\dfrac{20}{x+10}=\dfrac{1}{15}\)
=>\(\dfrac{20\left(x+10\right)-20x}{x\left(x+10\right)}=\dfrac{1}{15}\)
=>\(\dfrac{200}{x\left(x+10\right)}=\dfrac{1}{15}\)
=>x(x+10)=3000
=>\(x^2+10x-3000=0\)
=>(x+60)(x-50)=0
=>\(\left[{}\begin{matrix}x=-60\left(loại\right)\\x=50\left(nhận\right)\end{matrix}\right.\)
vậy: vận tốc dự định của ô tô là 50km/h

10≤n≤99↔21≤2n+1≤201
2n+1 là số chính phương nên
2n + 1 ∈{25;49;81;121;169}
=>n ∈ {12;24;40;60;84}
=> 3n + 1 ∈{37;73;121;181;253}
=> n = 40
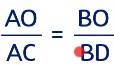
Giá 1kg táo trong tháng 1 là:
450000:18=25000(đồng)
Giá 1kg táo trong tháng 2 là:
420000:15=28000(đồng)
Giá trong tháng 2 so với tháng 1 thì tăng thêm:
28000-25000=3000(đồng)