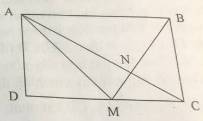
Cho hình vẽ, ABCD là hình chữ nhật có: MC = 2/5 DC = 10 cm; AD = 21 cm.
a) Tính diện tích hình thang ABCM;
b) Tính diện tích tam giác MNC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
Chiều cao của hình thang đó là:
336×2÷31+17=14( cm²)
Đáp số:14 cm².
Giải
Chiều cao của hình thang đó là:
336×2÷(31+17)=14( cm²)
Đáp số:14 cm².


\(\dfrac{x-1}{2}+\dfrac{x}{2}=x:2+\dfrac{1}{2}\)
\(\dfrac{x-1+x}{2}=\dfrac{x}{2}+\dfrac{1}{2}\)
\(\dfrac{2x-1}{2}=\dfrac{x+1}{2}\)
\(\dfrac{2x-1}{2}-\dfrac{x+1}{2}=0\)
\(\dfrac{2x-1-x-1}{2}=0\)
\(\dfrac{x-2}{2}=0\)
\(x-2=0.2=0\)
\(x=0+2=2\)
`<=> (2x-1)/2 = (x+1)/2`
`<=> 2x - 1 = x + 1
`<=> x = 2.`

tổng độ dài hai đáy là
412,5 x 2 : 15 = 55,4 (m)
đáy lớn là
55,4 - 20 = 35,4 (m)
\(CD=S_{ABCD}\times2:\left(AB\right)\)
\(\Rightarrow CD=412,5\times2:20\)
\(\Rightarrow CD=41,25m\)

Những số chia hết cho \(4\) là những số có tận cùng \(2\) chữ số chia hết cho \(4\) thì nó chia hết cho \(4\)
Những số chia hết cho \(5\) là những số có tận cùng là \(0\) hoặc \(5\)
Những số chia hết cho \(9\) là những số có tổng các chữ số chia hết cho \(9\)
Ta thử \(B=0\) mà \(90\) không chia hết cho \(4\) (Loại phương án này)
Ta thử \(B=5\) mà \(95\) không chia hết cho \(4\) (Loại phương án này)
Mà nếu đã không tìm được \(B\) thì sẽ không tìm được \(x\)
Vậy \(x\) không có giá trị nào để chia hết cho cả \(4;5\) và \(9\)

Diện tích hình tam giác EDC là :
13,5 x 10,2 : 2 = 68,85 ( m2 )
Đáp số : 68,85 m2

Diện tích giếng nước là: \(0,7\times0,7\times3,14=1,5386(m^2)\)
Diện tích của thành giếng đó là:
\(1,5386-(0,7-0,3)\times(0,7-0,3)\times3,14=1,0352(m^2)\)
a) MC = 2/5 DC nên DC = 5/2 MC = 5/2 . 10 = 25 cm.
Do đó, AB = CD = 25 cm.
Hình thang ABCM có hai đáy AB, CM và chiều cao BC = AD = 21 cm.
Diện tích hình thang ABCM bằng: (25 + 10) x 21 : 2 = 367,5 (cm2)
b) Hạ AH \(\perp\) BM, CK \(\perp\) BM.
Ta có \(\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{AB}{MC}=\dfrac{5}{2}\) (vì cùng chiều cao, tỉ lệ diện tích bằng tỉ lệ hai đáy), do đó \(\dfrac{AH}{CK}=\dfrac{S_{ABM}}{S_{BCM}}=\dfrac{5}{2}\) (chung đáy, tỉ lệ diện tích bằng tỉ lệ hai chiều cao)
\(\dfrac{S_{AMN}}{S_{CMN}}=\dfrac{AH}{CK}=\dfrac{5}{2}\Rightarrow\dfrac{S_{CMN}}{S_{AMC}}=\dfrac{2}{7}\)
\(S_{AMC}=\dfrac{1}{2}\times AD\times MC=\dfrac{1}{2}\times21\times10=105\left(cm^2\right)\)
\(S_{CMN}=\dfrac{2}{7}\times105=30\left(cm^2\right)\)