
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Vẽ đồ thị:
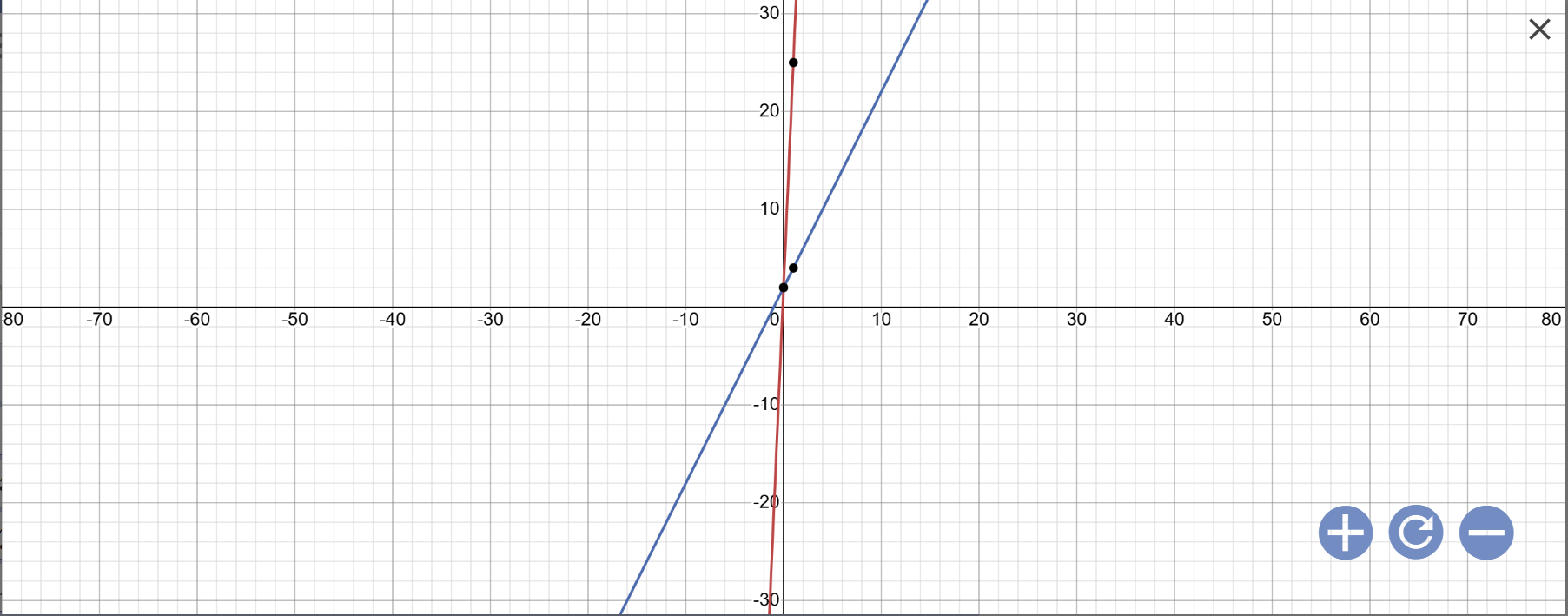
b: Tọa độ giao điểm của (d1) với trục Ox là:
\(\left\{{}\begin{matrix}y=0\\23x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\23x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{2}{23}\end{matrix}\right.\)
Tọa độ giao điểm của (d1) với trục Oy là:
\(\left\{{}\begin{matrix}x=0\\y=23x+2=23\cdot0+2=2\end{matrix}\right.\)
c: Phương trình hoành độ giao điểm là:
23x+2=2x+2
=>23x-2x=0
=>21x=0
=>x=0
Khi x=0 thì \(y=2x+2=2\cdot0+2=2\)
Vậy: (d1) cắt (d2) tại A(0;2)

`(-x^2 + x)/(-2x^2 + 3x - 1) ` `(đkxđ: x ne 1/2; x ne 1)`
`= (x^2 - x)/(2x^2 - 3x + 1) `
`= (x(x-1))/((x-1)(2x - 1))`
`= x/(2x -1)`
\(\dfrac{-x^2+x}{-2x^2+3x-1}\)
\(=\dfrac{x^2-x}{2x^2-3x+1}\)
\(=\dfrac{x\left(x-1\right)}{\left(2x-1\right)\left(x-1\right)}=\dfrac{x}{2x-1}\)

Chúng ta cần tìm giá trị lớn nhất và giá trị nhỏ nhất của hai hàm số đã chọn. ### **Câu a: \( F = \frac{2x + 3}{x^2 + 4} \)** #### **Bước 1: Tìm đạo hàm của \( F \)** Gọi: \[ F(x) = \frac{2x + 3}{x^2 + 4} \] Đạo hàm của \( F(x) \) theo quy tắc kinh tế: \[ F'(x) = \frac{(2)(x^2+4) - (2x+3)(2x)}{(x^2+4)^2} \] \[ = \frac{2x^2 + 8 - (4x^2 + 6x)}{(x^2+4)^2} \] \[ = \frac{-2x^2 - 6x + 8}{(x^2+4)^2} \] #### **Bước 2: Tìm các điểm cực trị** Phương pháp giải thích: \[ -2x^2 - 6x + 8 = 0 \] Chia hai vế cho -2: \[ x^2 + 3x - 4 = 0 \] \[ (x + 4)(x - 1) = 0 \] \[ x = -4, x = 1 \] #### **Bước 3: chắc hạn tại \( x \to \pm\infty \)** \[ \lim_{x \to \pm\infty} F(x) = 0 \] #### **Bước 4: Tính giá trị của \( F(x) \) tại các cực trị và một số điểm đặc biệt**### **Câu a: Tìm giá trị lớn nhất, nhỏ nhất của \( F = \frac{2x + 3}{x^2 + 4} \)** #### **Bước 1: Tìm đạo hàm của \( F(x) \)** Sử dụng quy tắc đạo hàm của một phân thức: \[ F(x) = \frac{2x + 3}{x^2 + 4} \] áp dụng công thức: \[ F'(x) = \frac{(2)(x^2 + 4) - (2x + 3)(2x)}{(x^2 + 4)^2} \] \[ = \frac{2x^2 + 8 - (4x^2 + 6x)}{(x^2 + 4)^2} \] \[ = \frac{-2x^2 - 6x + 8}{(x^2 + 4)^2} \] #### **Bước 2: Tìm các cực trị** Giải thích phương trình \( F'(x) = 0 \): \[ -2x^2 - 6x + 8 = 0 \] Chia hai vế cho -2: \[ x^2 + 3x - 4 = 0 \] Phân tích thành nhân tử: \[ (x + 4)(x - 1) = 0 \] \[ x = -4, x = 1 \] #### **Bước 3: dừng giới hạn tại \( x \to \pm\infty \)** \[ \lim_{x \to \pm\infty} F(x) = 0 \] Do đó đồ thị có đỉnh ngang là \( y = 0 \). #### **Bước 4: Tính giá trị của \( F(x) \) tại các cực trị** \[ F(-4) =

Olm chào em, em xem hướng dẫn chi tiết dưới đây em sẽ hiểu vì sao em nhé.
Giải:
\(x^2\) - 5\(x\) + 6
= (\(x^2\) - 3\(x\)) - (2\(x-6\))
= \(x\left(x-3\right)-2\left(x-3\right)\)
= (\(x-3\))(\(x-2\))

1: Để (d) cắt (d') tại một điểm trên trục tung thì
\(\left\{{}\begin{matrix}a\ne a'\\b=b'\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne m-2\\m-1=-2m\end{matrix}\right.\Leftrightarrow3m=1\)
=>\(m=\dfrac{1}{3}\)
2: Thay x=2 vào y=mx+m-1, ta được:
\(y=m\cdot2+m-1=3m-1\)
Thay x=2 và y=3m-1 vào (d'), ta được:
\(2\left(m-2\right)-2m=3m-1\)
=>3m-1=-4
=>3m=-3
=>m=-1
3: Thay x=-1 và y=2 vào (d), ta được:
\(m\cdot\left(-1\right)+m-1=2\)
=>-m+m-1=2
=>-1=2(vô lý)
vậy: \(m\in\varnothing\)

Giải:
Số trái cây sầu riêng cửa hàng đã bán được là:
400 x 20 : 100 = 80 (kg)
Kết luận số trái cây sầu riêng cửa hàng đã bán là 80 kg.

Các tỉ số theo định lí Thales là:
1; \(\frac{BD}{BA}\) = \(\frac{BE}{AC}\)
2; \(\frac{BD}{DA}\) = \(\frac{BE}{EC}\)
3; \(\frac{DA}{BA}\) = \(\frac{EC}{BC}\)

\(x^2-9x+8=0\)
=>\(x^2-x-8x+8=0\)
=>x(x-1)-8(x-1)=0
=>(x-1)(x-8)=0
=>\(\left[{}\begin{matrix}x-1=0\\x-8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=8\end{matrix}\right.\)
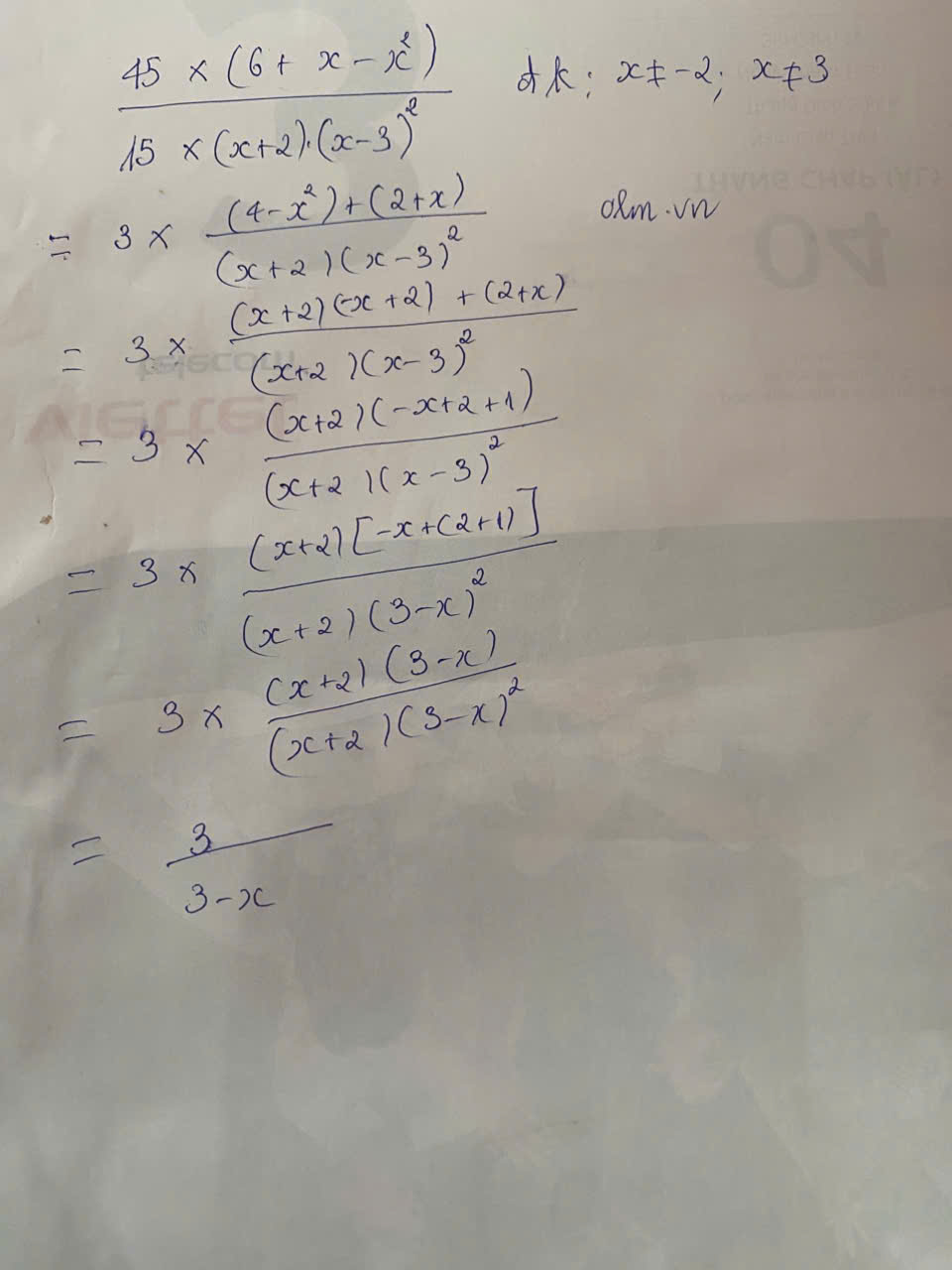
Ta có: MNPQ là hình bình hành
=>MP cắt NQ tại trung điểm của mỗi đường
=>O là trung điểm chung của MP và NQ
Xét ΔMQN có
ND,MO là các đường trung tuyến
ND cắt MO tại H
do đó: H là trọng tâm của ΔMQN
=>\(NH=\frac23ND\)
Xét ΔNQP có
NE,PO là các đường trung tuyến
NE cắt PO tại K
Do đó: K là trọng tâm của ΔNQP
=>\(NK=\frac23NE\)
Xét ΔNDE có \(\frac{NH}{ND}=\frac{NK}{NE}\left(=\frac23\right)\)
nên HK//DE
=>\(\frac{HK}{DE}=\frac{NH}{ND}=\frac23\)
=>\(\frac{28}{DE}=\frac23=\frac{28}{42}\)
=>DE=42(cm)