`3^3 - 2^2 . 5 + 125 : 5`

`= 27 - 4 . 5 +` \(\dfrac{125}{52}\)

`= 27 - 20 +` \(\dfrac{125}{52}\)

`= 7 +` \(\dfrac{125}{52}\)

`=` \(\dfrac{7.52+125}{52}\)

`=` \(\dfrac{489}{52}\)

\(3^3-2^2\cdot5+125:52\)

= \(27-4\cdot5+\dfrac{125}{52}\)

= \(27-20+\dfrac{125}{52}\)

= \(7+\dfrac{125}{52}\)

= \(\dfrac{52\cdot7+125}{52}\)

= \(\dfrac{489}{52}\)

Kẻ tia `Ot` là tia đối của tia `Ox`

=> \(\widehat{xOt}=180^o\)

Ta có: 

\(\widehat{yOt}=\widehat{xOt}-\widehat{xOy}=180^o-120^o=60^o\)

=> \(\widehat{tOz}=\widehat{zOy}-\widehat{yOt}=134^o-60^o=74^o\)

Mà \(\widehat{xOz};\widehat{zOt}\) là 2 góc kề bù

=> \(\widehat{zOx}+\widehat{zOt}=\widehat{xOt}\)

=> \(\widehat{xOz}=\widehat{xOt}-\widehat{tOz}=180^o-74^o=106^o\)

Vậy ...

Để giải phương trình này, chúng ta cần sử dụng phương pháp thử với các giá trị $n$ khác nhau hoặc giải bằng cách số học chi tiết.

Tuy nhiên, ta có thể nhận thấy rằng phương trình này có thể được giải bằng cách kiểm tra từng nhóm số. Bạn muốn mình giải phương trình này một cách cụ thể hay chỉ dừng ở đây?

`(x + 7) - 25 = 13`

`=> x +7 = 13 + 25`

`=> x+ 7 = 38`

`=> x = 38 - 7`

`=> x = 31`

Vậy `x=31`

\(\left(x+7\right)-25=13\)

\(x+7=13+25\)

\(x+7=38\)

\(x=38-7\)

\(x=31\)

vậy x = 31

Vòi 1 trong 1 giờ chảy được số phần bể là: 

`1 : 8 =` \(\dfrac{1}{8}\) (bể)

Vòi 2 trong 1 giờ chảy được số phần bể là: 

`1 : 6 =` \(\dfrac{1}{6}\) (bể)

Vòi 3 trong 1 giờ tháo được số phần bể là: 

`1 : 4 =` \(\dfrac{1}{4}\) (bể)

Cả 3 vòi cùng hoạt động thì trong 1 giờ chảy được số phần bể là: 

\(\dfrac{1}{8}+\dfrac{1}{6}-\dfrac{1}{4}=\dfrac{1}{24}\) (bể) 

Đáp số: ...

\(\dfrac{1}{2}\times\dfrac{1}{3}+\dfrac{1}{4}:\dfrac{1}{5}=\dfrac{1}{6}+\dfrac{1}{4}\times5=\dfrac{1}{6}+\dfrac{5}{4}=\dfrac{2}{12}+\dfrac{15}{12}=\dfrac{17}{12}\)

a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có

BD chung

\(\widehat{ABD}=\widehat{MBD}\)

Do đó: ΔBAD=ΔBMD

b: ΔBAD=ΔBMD

=>DA=DM

mà DM<DC(ΔDMC vuông tại M)

nên DA<DC

c: XétΔBKC có

KM,CA là các đường cao

KM cắt CA tại D

Do đó: D là trực tâm của ΔBKC

=>BD\(\perp\)KC tại N

Xét ΔDAK vuông tại A và ΔDMC vuông tại M có

DA=DM

\(\widehat{ADK}=\widehat{MDC}\)(hai góc đối đỉnh)

Do đó: ΔDAK=ΔDMC

=>DK=DC

=>ΔDKC cân tại D

\(x^2-9x-26=0\)

\(\text{Δ}=\left(-9\right)^2-4\cdot1\cdot\left(-26\right)=81+104=185>0\)

Do đó: Phương trình có hai nghiệm phân biệt là:

\(\left[{}\begin{matrix}x=\dfrac{9-\sqrt{185}}{2}\\x=\dfrac{9+\sqrt{185}}{2}\end{matrix}\right.\)

TY :>

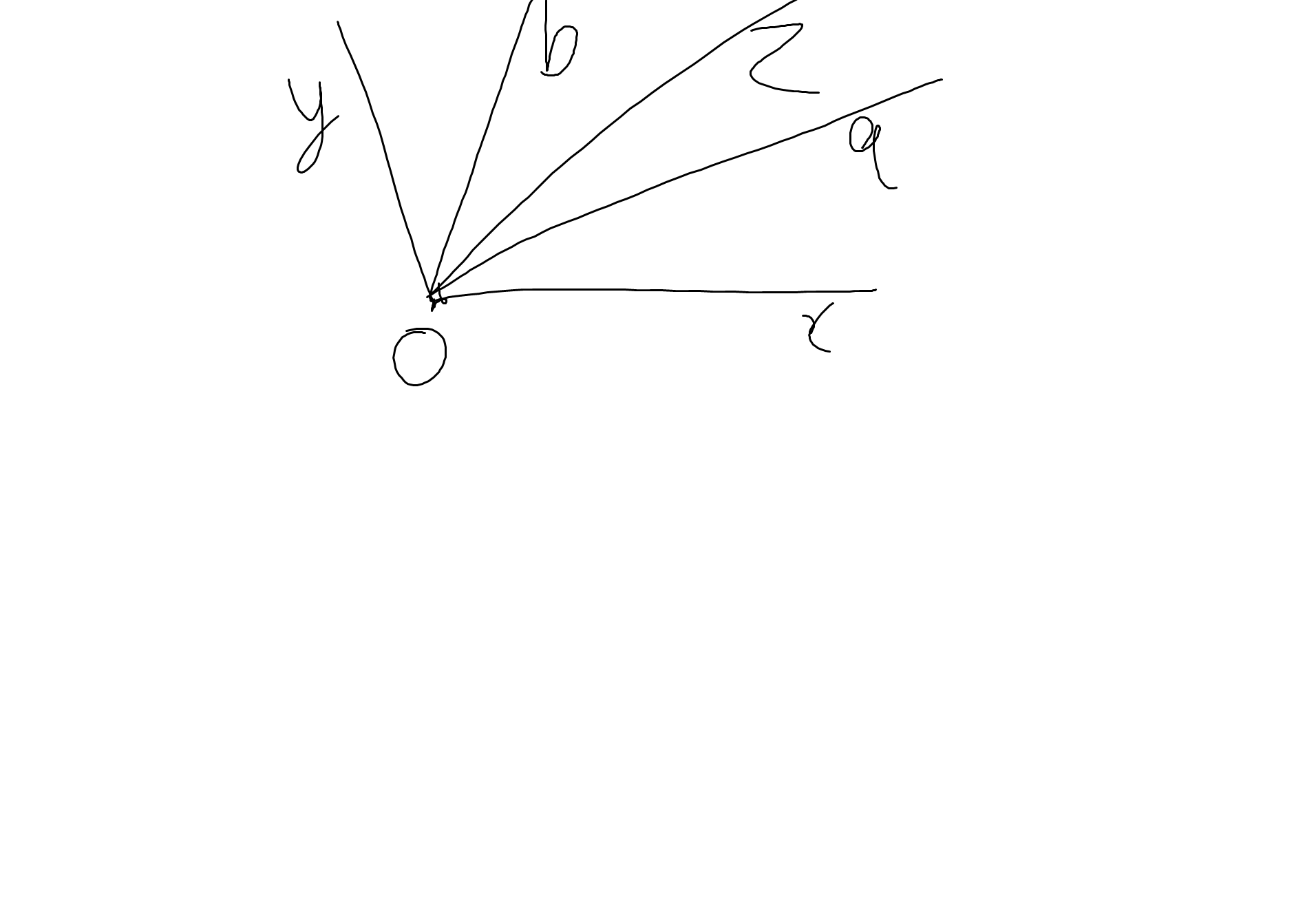
Oa là phân giác của góc xOz

=>\(\widehat{zOa}=\dfrac{\widehat{xOz}}{2}\)

Ob là phân giác của góc zOy

=>\(\widehat{zOb}=\dfrac{\widehat{zOy}}{2}\)

\(\widehat{aOb}=\widehat{zOa}+\widehat{zOb}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{zOy}\right)\)

\(=\dfrac{1}{2}\cdot\widehat{xOy}=\dfrac{1}{2}\cdot150^0=75^0\)

`(a_1 + a_2+... + a_9)/(a_3+a_6+a_9)`

`= ((a_3+a_6+a_9) + (a_2+a_5+a_8) + (a_1+a_4+a_7))/(a_3+a_6+a_9)`

`<= (3.(a_3+a_6+a_9))/(a_3+a_6+a_9) = 3 < 5`.