Cho hình bình hành ABCD. Gọi M, N thứ tự là trung điểm của các cạnh AB, BC. DM cắt AC ở I, DN cắt AC ở K. Chứng minh: AI = IK = KC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài `1`
\(a,5x^2-10xy=5x\left(x-2y\right)\\ b,3x\left(x-y\right)-6\left(x-y\right)=\left(x-y\right)\left(3x-6\right)\\ =3\left(x-y\right)\left(x-2\right)\\ c,2x\left(x-y\right)-4y\left(y-x\right)=2x\left(x-y\right)+4y\left(x-y\right)\\ =\left(x-y\right)\left(2x+4y\right)=2\left(x-y\right)\left(x+2y\right)\\ d,9x^2-9y^2=\left(3x\right)^2-\left(3y\right)^2=\left(3x-3y\right)\left(3x+3y\right)\\ f,xy-xz-y+z=\left(xy-xz\right)-\left(y-z\right)\\ =x\left(y-z\right)-\left(y-z\right)=\left(y-z\right)\left(x-1\right)\)
Bài `3`
\(a,3x^2+8x=0\\ \Leftrightarrow x\left(3x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x+8=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\3x=-8\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{8}{3}\end{matrix}\right.\)
\(b,9x^2-25=0\\ \Leftrightarrow\left(3x\right)^2-5^2=0\\ \Leftrightarrow\left(3x-5\right)\left(3x+5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}3x-5=0\\3x+5=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=5\\3x=-5\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(c,x^3-16x=0\\ \Leftrightarrow x\left(x^2-16\right)=0\\ \Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x-4=0\\x+4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
\(d,x^3+x=0\\ \Leftrightarrow x\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+1\in\varnothing\\x=0\end{matrix}\right.\Rightarrow x=0\)

a) (a - 2b)x(a + 2b)
b) x2-(y-3)2
=> (x-y+3)(x+y-3)
c) (2a + b - a)(2a + b + a)
=> (a+b)(3a+b)
d) (4(x - 1))2 - (5(x + y))2
⇔ (4x - 4 - 5x - 5y)(4x - 4 + 5x + 5y)
⇔ -(x + 5y + 4)(9x + 5y + -4)
e) (x + 5)2
f) (5x - 2y)2
h) (x - 5)(x2 + 5x + 25)
k) (x + 5)3

Lời giải:
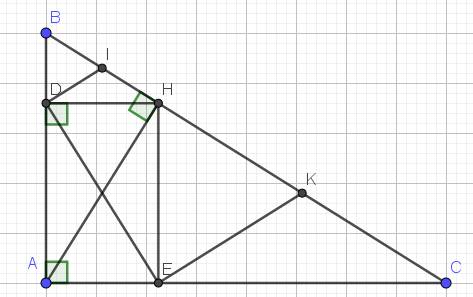
a. Xét tứ giác $ADHE$ có 3 góc vuông $\widehat{A}=\widehat{D}=\widehat{E}=90^0$ nên tứ giác $ADHE$ là hình chữ nhật.
b.
Xét tam giác vuông $BDH$ vuông tại $D$ có $DI$ là đường trung tuyến ứng với cạnh huyền $BH$ nên $DI=\frac{BH}{2}=IH$
$\Rightarrow DIH$ là tam giác vuông tại $I$
$\Rightarrow \widehat{IDH}=\widehat{IHD}$ (1)
$ADHE$ là hình chữ nhật nên $\widehat{HDE}=\widehat{HAE}=\widehat{HAC}$ (2)
Từ $(1); (2)\Rightarrow \widehat{IDH}+\widehat{HDE}=\widehat{IHD}+\widehat{HAC}$
$\Rightarrow \widehat{IDE}=\widehat{IHD}+\widehat{HAC}$.
Mà $\widehat{IHD}=\widehat{HCA}$ (2 góc đồng vị)
$\Rightarrow \widehat{IDE}=\widehat{HCA}+\widehat{HAC}=180^0-\widehat{AHC}=180^0-90^0=90^0$
$\Rightarrow DI\perp DE$
c. Tương tự phần a ta suy ra $DE\perp EK$
Vậy $DI\perp DE, EK\perp DE$
$\Rightarrow DI\parallel EK$ và $DI, EK$ cùng vuông góc với $DE$
$\Rightarrow DIKE$ là hình thang vuông.
d.
Có: $DI=\frac{BH}{2}\Rightarrow BH=2DI=2.1=2$ (cm)
$EK=\frac{CH}{2}\Rightarrow CH=2EK=8$ (cm)
$\Rightarrow BC=BH+CH=2+8=10$ (cm)
$S_{ABC}=AH.BC:2=6.10:2=30$ (cm2)

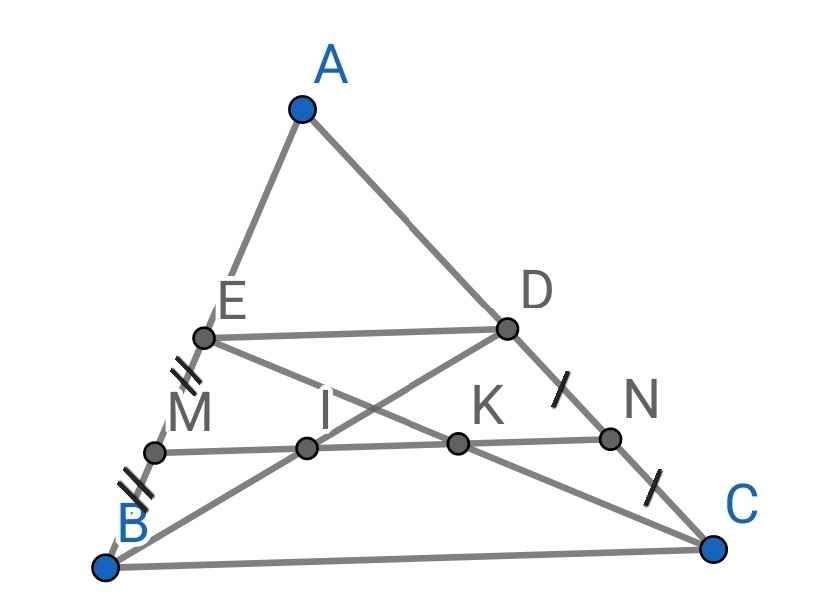
Do BD là đường trung tuyến của ∆ABC (gt)
⇒ D là trung điểm của AC
Do CE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AB
⇒ DE là đường trung bình của ∆ABC
⇒ DE // BC và DE = BC : 2
⇒ BC = 2DE
Do DE // BC (cmt)
⇒ BCDE là hình thang
Do M là trung điểm của BE (gt)
N là trung điểm của CD (gt)
⇒ MN là đường trung bình của hình thang BCDE
⇒ MN // DE // BC và MN = (DE + BC) : 2
Do MN // DE (cmt)
⇒ MI // DE và NK // DE
∆BDE có:
MI // DE (cmt)
M là trung điểm của BE (gt)
⇒ I là trung điểm của BD
⇒ MI là đường trung bình của ∆BDE
⇒ MI = DE : 2 (1)
∆CDE có:
NK // DE (cmt)
N là trung điểm của CD (gt)
⇒ K là trung điểm của CE
⇒ NK là đường trung bình của ∆CDE
⇒ NK = DE : 2 (2)
Mà MI = DE : 2
⇒ MI = NK = DE : 2
⇒ MI + NK = DE
Ta có:
MN = (DE + BC) : 2
Mà BC = 2DE (cmt)
⇒ MN = (DE + 2DE) : 2
= DE + DE : 2
Lại có:
MN = MI + IK + NK
= (MI + NK) + IK
= DE + IK
⇒ DE + IK = DE + DE : 2
⇒ IK = DE : 2 (3)
Từ (1), (2) và (3) ⇒ MI = IK = KN
Xét Δ���ΔBED có {��//����=��{MI//EDME=BM suy ra ��=��ID=IB.
Xét Δ���ΔCED có {��//����=��{NK//EDNC=ND suy ra ��=��KE=KC.
Suy ra ��=12��MI=21ED; ��=12��NK=21ED; ��=12��ED=21BC.
��=��−��=12��−12��=��−12��=12��IK=MK−MI=21BC−21DE=DE−21DE=21DE.
Vậy ��=��=��MI=IK=KN.

A B C M N G D E
a/
Xét tg ABC có
NA=NB; MA=MC => MN là đường trung bình của tg ABC => MN//BC
Xét tg GBC có
DG=DB; EG=EC => DE là đường trung bình của tg GBC => DE//BC
=> MN//DE (cùng // BC)
b/
Xét tg ABG có
NA=NB; DG=DB => ND là đường trung bình của tg ABG => ND//AG
Xét tg ACG có
MA=MC; EG=EC => ME là đường trung bình của tg ACG => ME//AG
=> ND//ME (cùng // với AG)
a) Vì ��BM, ��CN là các đường trung tuyến của Δ���ΔABC nên ��=��MA=MC, ��=��NA=NB.
Do đó ��MN là đường trung bình của Δ ���Δ ABC, suy ra ��MN // ��BC. (1)
Ta có ��DE là đường trung bình của Δ ���Δ GBC nên ��DE // ��BC. (2)
Từ (1) và (2) suy ra ��MN // ��DE.
b) Xét Δ ���Δ ABG, ta có ��ND là đường trung bình.
Xét Δ ���Δ ACG, ta có ��ME là đường trung bình.
Do đó ��ND // ��AG, ��ME // ��AG.
Suy ra ��ND // ��ME.

A B C D M O E
a/ Goi E là trung điểm của MC
Từ gt \(AM=\dfrac{1}{2}MC\Rightarrow AM=ME=EC\)
Xét tg BCM có
ME=EC (cmt); DB=DC (gt) => DE là đường trung bình của tg BCM
=> DE//BM
Xét tg ADE có
AM=ME (cmt)
BM//DE (cmt) =>OM//DE
=> OA=OD (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
b/
Ta có DE là đường trung bình của tg BCM \(\Rightarrow DE=\dfrac{1}{2}BM\)
Xét tg ADE có
OA=OD (cmt); AM=ME (cmt) => OM là đường trung bình của tg ADE
\(\Rightarrow OM=\dfrac{1}{2}DE=\dfrac{1}{2}.\dfrac{1}{2}BM=\dfrac{1}{4}BM\)
a) Qua �D vẽ một đường thẳng song song với ��BM cắt ��AC tại �N.
Xét Δ ���Δ MBC có ��=��DB=DC và ��DN // ��BM nên ��=��=12��MN=NC=21MC (định lí đường trung bình của tam giác).
Mặt khác ��=12��AM=21MC, do đó ��=��=12��AM=MN=21MC.
Xét Δ ���Δ AND có ��=��AM=MN và ��BM // ��DN nên ��=��OA=OD hay �O là trung điểm của ��AD.
b) Xét Δ ���Δ AND có ��OM là đường trung bình nên ��=12��OM=21DN. (1)
Xét Δ ���Δ MBC có ��DN là đường trung bình nên ��=12��DN=21BM. (2)
Từ (1) và (2) suy ra ��=14��OM=41BM.

Gọi K là trung điểm của CD
a: Xét ΔBDC có
M là trung điểm của BC
K là trung điểm của CD
Do đó: MK là đường trung bình
=>MK//BD
hay ID//MK
Xét ΔAMK có
I là trung điểm của AM
ID//MK
Do đó: D là trung điểm của AK
=>AD=DK=KC
=>AD=1/2DC
b: Xét ΔAMK có
I là trung điểm của AM
D là trung điểm của AK
Do đó: ID là đường trung bình
=>ID=MK/2
hay MK=2ID
Ta có: MK là đường trung bình của ΔBDC
nên MK=BD/2
=>BD/2=2ID
hay BD=4ID
Đúng thầy cho em like nhé !
a) Kẻ ��MN // ��BD, �∈��N∈AC.
��MN là đường trung bình trong △���△CBD
Suy ra �N là trung điểm của ��CD (1).
��IN là đường trung bình trong △���△AMN
Suy ra �D là trung điểm của ��AN (2).
Từ (1) và (2) suy ra ��=12��AD=21DC.
b) Có ��=12��ID=21MN; ��=12��MN=21BD, nên ��=��BD=ID.



367+1290{36:6}?