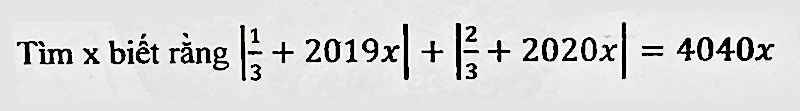
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{5^2}{1\cdot6}+\dfrac{5^2}{6\cdot11}+...+\dfrac{5^2}{26\cdot31}\)
\(=5\left(\dfrac{5}{1\cdot6}+\dfrac{5}{6\cdot11}+...+\dfrac{5}{26\cdot31}\right)\)
\(=5\left(1-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{11}+...+\dfrac{1}{26}-\dfrac{1}{31}\right)\)
\(=5\left(1-\dfrac{1}{31}\right)=5\cdot\dfrac{30}{31}=\dfrac{150}{31}\)

\(25M=\dfrac{5^{12}+25}{5^{12}+1}=1+\dfrac{24}{5^{12}+1}\)
\(25N=\dfrac{5^{20}}{5^{20}+1}=\dfrac{5^{20}+1-1}{5^{20}+1}=1-\dfrac{1}{5^{20}+1}\)
\(\dfrac{24}{5^{12}+1}>\dfrac{-1}{5^{20}+1}\)
=>\(\dfrac{24}{5^{12}+1}+1>\dfrac{-1}{5^{20}+1}+1\)
=>25M>25N
=>M>N

x×4+x=55,35�×4+�=55,35
x×4+x×1=55,35�×4+�×1=55,35
x×(4+1)=55,35�×(4+1)=55,35
x×5=55,35�×5=55,35
x=55,35:5�=55,35:5
x=11,07�=11,07
Vậy x = 11,07`
x×4+x=55,35�×4+�=55,35
x×4+x×1=55,35�×4+�×1=55,35
x×(4+1)=55,35�×(4+1)=55,35
x×5=55,35�×5=55,35
x=55,35:5�=55,35:5
x=11,07�=11,07
Vậy x = 11,07`

đổi 20 phút=1/3 giờ
quãng đường từ nhà đến trừng là:
1,2*1/3=0,4(km)
thời gian huy đi từ nhà đến trường vào sáng nay là:
10+20=30 phút
Vận tốc sáng nay của Huy là:
0,4:30=1/75(km/s)

Tổng của các số từ 1 đến 2024 là:
\(\dfrac{2024\left(2024+1\right)}{2}=1012\cdot2025⋮2\)
=>Tổng là số chẵn

Giải:
Cứ 1 đường thẳng tạo với 15 - 1 đường thẳng còn lại số góc nhỏ hơn góc bẹt là: 15 - 1 góc
Với 15 đường thẳng sẽ tạo được số góc nhỏ hơn góc bẹt là:
(15 - 1) x 15 = 210 (góc)
Đáp số: 210 góc

bài 9:
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)
Do đó: ΔAHB~ΔBCD
b: ta có: ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD^2=9^2+12^2=225=15^2\)
=>BD=15(cm)
Ta có: ΔAHB~ΔBCD
=>\(\dfrac{AH}{BC}=\dfrac{AB}{BD}\)
=>\(\dfrac{AH}{9}=\dfrac{12}{15}\)
=>\(AH=9\cdot\dfrac{12}{15}=9\cdot\dfrac{4}{5}=7,2\left(cm\right)\)
Bài 10:
a: Xét ΔOEA vuông tại E và ΔODB vuông tại D có
\(\widehat{EOA}=\widehat{DOB}\)(hai góc đối đỉnh)
Do đó: ΔOEA~ΔODB
=>\(\dfrac{OE}{OD}=\dfrac{OA}{OB}\)
=>\(OE\cdot OB=OA\cdot OD\)
b: Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
\(\widehat{ECB}\) chung
Do đó: ΔCEB~ΔCDA
=>\(\dfrac{CE}{CD}=\dfrac{CB}{CA}\)
=>\(\dfrac{CE}{CB}=\dfrac{CD}{CA}\)
Xét ΔCED và ΔCBA có
\(\dfrac{CE}{CB}=\dfrac{CD}{CA}\)
\(\widehat{ECD}\) chung
Do đó: ΔCED~ΔCBA

Lời giải:
Vì $|\frac{1}{3}+2019x|+|\frac{2}{3}+2020x|\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow 4040x\geq 0\Rightarrow x\geq 0$
$\Rightarrow |\frac{1}{3}+2019x|=\frac{1}{3}+2019x; |\frac{2}{3}+2020x|=\frac{2}{3}+2020x$
Bài toán trở thành:
$\frac{1}{3}+2019x+\frac{2}{3}+2020x=4040x$
$\Rightarrow 1+4039x=4040x$
$\Rightarrow x=1$ (tm)