Oa là phân giác của góc xOz

=>\(\widehat{zOa}=\dfrac{\widehat{xOz}}{2}\)

Ob là phân giác của góc zOy

=>\(\widehat{zOb}=\dfrac{\widehat{zOy}}{2}\)

\(\widehat{aOb}=\widehat{zOa}+\widehat{zOb}=\dfrac{1}{2}\left(\widehat{xOz}+\widehat{zOy}\right)\)

\(=\dfrac{1}{2}\cdot\widehat{xOy}=\dfrac{1}{2}\cdot150^0=75^0\)

Kẻ tia `Ot` là tia đối của tia `Ox`

=> \(\widehat{xOt}=180^o\)

Ta có: 

\(\widehat{yOt}=\widehat{xOt}-\widehat{xOy}=180^o-120^o=60^o\)

=> \(\widehat{tOz}=\widehat{zOy}-\widehat{yOt}=134^o-60^o=74^o\)

Mà \(\widehat{xOz};\widehat{zOt}\) là 2 góc kề bù

=> \(\widehat{zOx}+\widehat{zOt}=\widehat{xOt}\)

=> \(\widehat{xOz}=\widehat{xOt}-\widehat{tOz}=180^o-74^o=106^o\)

Vậy ...

Bài 3: Các cặp góc so le trong là: \(\widehat{tBO};\widehat{BOC}\); \(\widehat{OBC};\widehat{yOB}\); \(\widehat{BCO};\widehat{x'OC}\); \(\widehat{t'CO};\widehat{BOC}\)

Các cặp góc đồng vị là:

\(\widehat{xBt};\widehat{xOy}\); \(\widehat{tBO};\widehat{x'Oy}\); \(\widehat{y'Ct'};\widehat{x'Oy'}\); \(\widehat{t'CO};\widehat{x'Oy}\)

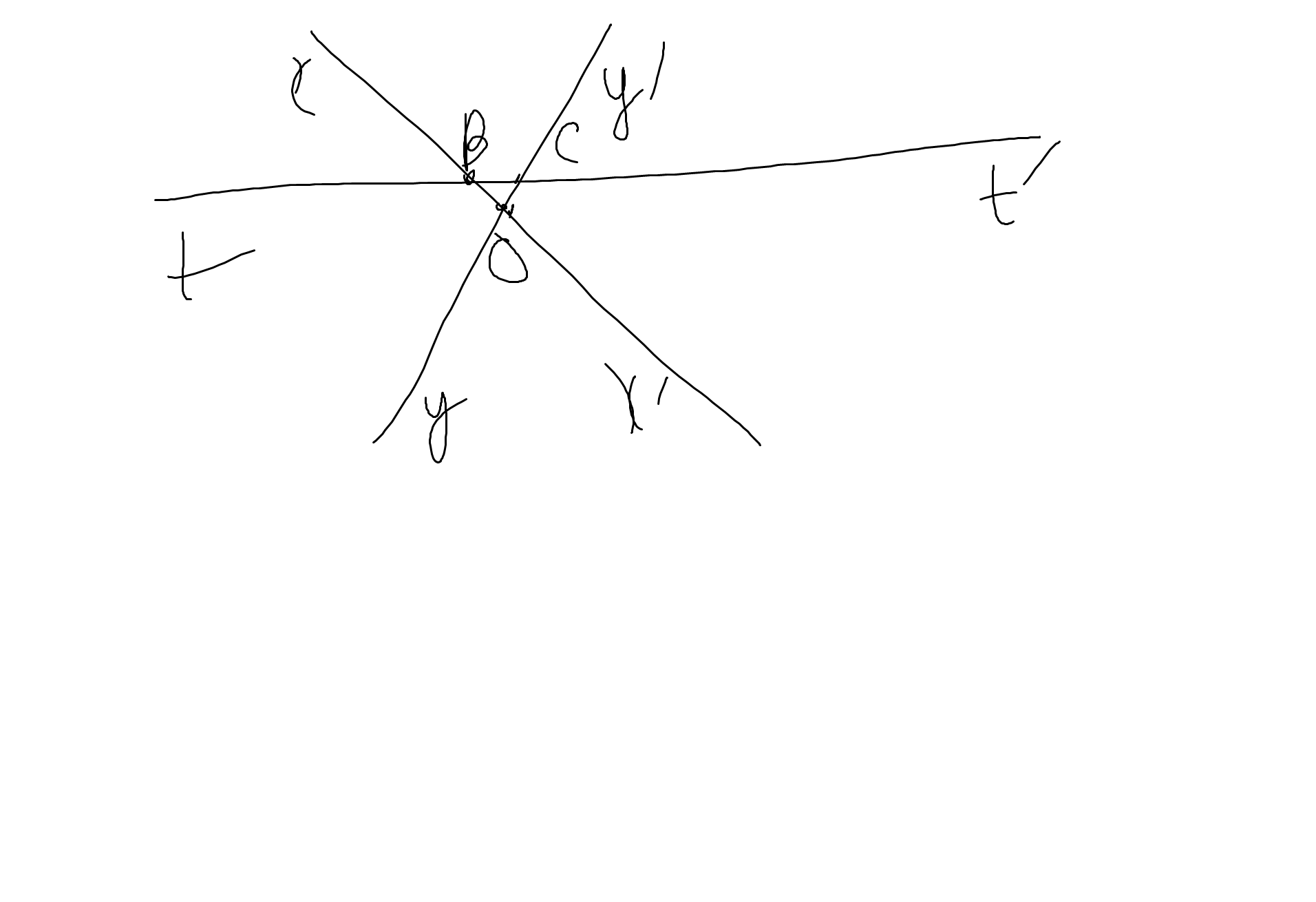
Bài 2: 

Các cặp góc so le trong là \(\widehat{FEC};\widehat{ACB}\)

Các cặp góc đồng vị là \(\widehat{ADE};\widehat{ABC}\); \(\widehat{AED};\widehat{ACB}\)

Các cặp góc trong cùng phía là: \(\widehat{BDE};\widehat{B}\); \(\widehat{DEC};\widehat{ECB}\)

\(x^3+ax+b\\ =\left(x^3+4x^2+3x\right)+\left(-4x^2-16x-12\right)+\left(a+13\right)x+\left(b+12\right)\\ =x\left(x^2+4x+3\right)-4\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\\ =\left(x-4\right)\left(x^2+4x+3\right)+\left(a+13\right)x+\left(b+12\right)\)

Để `x^3+ax+b` chia hết cho `x^2+4x+3` thì:

\(\left\{{}\begin{matrix}a+13=0\\b+12=0\end{matrix}\right.=>\left\{{}\begin{matrix}a=-13\\b=-12\end{matrix}\right.\)

Ta có: 

\(1+2+3+...+n\)

Số lượng số hạng là: `(n-1):1+1=n` (số hạng) 

Tổng của dãy số là: `(n+1)*n/2` 

Áp dụng ta có:

\(\dfrac{1}{1+2+3}+\dfrac{1}{1+2+3+4}+....+\dfrac{1}{1+2+3+...+100}\\ =\dfrac{1}{\dfrac{3\cdot\left(3+1\right)}{2}}+\dfrac{1}{\dfrac{4\cdot\left(4+1\right)}{2}}+...+\dfrac{1}{\dfrac{100\cdot\left(100+1\right)}{2}}\\ =\dfrac{2}{3\cdot4}+\dfrac{2}{4\cdot5}+...+\dfrac{2}{100\cdot101}\\ =2\left(\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+...+\dfrac{1}{100\cdot101}\right)\\ =2\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{100}-\dfrac{1}{101}\right)\\ =2\left(\dfrac{1}{3}-\dfrac{1}{101}\right)\\ =2\cdot\dfrac{98}{303}\\ =\dfrac{196}{303}\)

trả lời xong nhớ cho coin

ko bế ơi

like thôi

quan trao đổi khí ở động vật là bề mặt cơ thể, mang, hệ thống ống khí, phổi.

Cơ quan trao đổi khí ở thực vật là tất cả các bộ phận có khả năng thấm khí của cơ thể. Tuy nhiên, trao đổi khí giữa cơ thể thực vật với môi trường chủ yếu thông qua các khí khổng ở lá và bì khổng (lỗ vỏ) ở thân cây.

+ So sánh sự trao đổi khí ở cơ thể thực vật và cơ thể động vật:

    • Giống nhau: Lấy O2 và thải CO2

    • Khác nhau:

      - Trao đổi khí giữa cơ thể thực vật với môi trường được thực hiện chủ yếu thông qua các khí khổng ở lá và bì khổng ở thân cây. Động vật trao đổi khí với môi trường xung quanh nhờ cơ quan hô hấp, đó là bề mặt cơ thể, hệ thống ống khí, mang, phổi.

      - Động vật chỉ trao đổi khí với môi trường nhờ quá trình hô hấp (lấy khí O2, thải khí CO2). Thực vật trao đổi khí với môi trường nhờ cả hô hấp (lấy khí O2, thải khí CO2) và quang hợp (lấy khí CO2, thải khí O2)

Bài tập lấy ở đâu vậy bạn 

a: Ta có: \(\widehat{bMB}=\widehat{NMC}\)(hai góc đối đỉnh)

mà \(\widehat{bMB}=50^0\)

nên \(\widehat{NMC}=50^0\)

Ta có: \(\widehat{MNC}+\widehat{aNC}=180^0\)(hai góc kề bù)

=>\(\widehat{MNC}+110^0=180^0\)

=>\(\widehat{MNC}=70^0\)

Xét ΔMNC có \(\widehat{NMC}+\widehat{MNC}+\widehat{C}=180^0\)

=>\(\widehat{C}+50^0+70^0=180^0\)

=>\(\widehat{C}=60^0\)

b: Ta có: \(\widehat{NMB}+\widehat{NMC}=180^0\)(hai góc kề bù)

=>\(\widehat{NMB}+50^0=180^0\)

=>\(\widehat{NMB}=130^0\)

Ta có: MN//AB

=>\(\widehat{CMN}=\widehat{CBA}\)(hai góc đồng vị)

=>\(\widehat{CBA}=50^0\)

BN là phân giác của góc CBA

=>\(\widehat{NBM}=\dfrac{\widehat{ABC}}{2}=25^0\)

Xét ΔNMB có \(\widehat{NMB}+\widehat{BNM}+\widehat{NBM}=180^0\)

=>\(\widehat{MNB}=180^0-130^0-25^0=25^0\)

c: BN là phân giác của góc CBA

=>\(\widehat{ABN}=\dfrac{\widehat{ABC}}{2}=25^0\)

Xét ΔABC có \(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^0\)

=>\(\widehat{BAN}+60^0+50^0=180^0\)

=>\(\widehat{BAN}=70^0\)

Xét ΔBAN có \(\widehat{BAN}+\widehat{ABN}+\widehat{ANB}=180^0\)

=>\(\widehat{ANB}=180^0-75^0-25^0=85^0\)

Bài 1:

a: \(\dfrac{a}{b}>1\)

=>\(\dfrac{a}{b}-1>0\)

=>\(\dfrac{a-b}{b}>0\)

mà b>0

nên a-b>0

=>a>b

b: a>b

=>\(\dfrac{a}{b}>\dfrac{b}{b}\)

=>\(\dfrac{a}{b}>1\)

c: a/b<1

=>\(\dfrac{a}{b}-1< 0\)

=>\(\dfrac{a-b}{b}< 0\)

mà b>0

nên a-b<0

=>a<b

d: a<b

=>\(\dfrac{a}{b}< \dfrac{b}{b}\)

=>\(\dfrac{a}{b}< 1\)