Tìm số tự nhiên n khác 0 để \(A=2n^3-3n+1\) là số nguyên tố
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì y = y => tam giác trên vuông cân
Trong tam giác cân , đường cao là đường trung tuyến , đường trung trực , đường phân giác
Trong tam giác vuông cân , đường trung tuyến = 1/2 cạnh huyền
=> đường trung tuyến = x =5
Theo định lý pitago tong tam giác vuông => 52 + x2 = y2
25 + 52 = y2
25 + 25 = y2
50 = y2 => y = \(\sqrt{50}\)
Vậy x = 5 , y = \(\sqrt{50}\)
Ta có: \(\frac{1}{5^2}=\frac{1}{y^2}+\frac{1}{y^2}=\frac{2}{y^2}\Rightarrow y=5\sqrt{2}\)
\(x^2+5^2=y^2=\left(5\sqrt{2}\right)^2=2.5^2\Rightarrow x=5\).

Đáp án+Giải thích các bước giải:
Bài 11:
a)x=30x+15a)x=30x+15 (nghìn đồng)
b)b) Vì An được giảm 10%10% và phải trả 121,5121,5 nghìn đồng nên ta có:
(100%−10%)x=121,5(100%-10%)x=121,5
⇔90%x=121,5⇔90%x=121,5
mà x=30x+15x=30x+15
⇒(30x+15).90%=121,5⇒(30x+15).90%=121,5
⇔(30x+15).0,9=121,5⇔(30x+15).0,9=121,5
⇔30x+15=135⇔30x+15=135
⇔ 30x=120⇔ 30x=120
⇔x=4(t⇔x=4(t/m)/m)
Vậy An đã mua 44 ly trà sữa

(*) \(\Leftrightarrow4sinx.cosx+1=sinx-cosx\)
Đặt a = sin x ; b = cos x \(\left(-1\le a;b\le1\right)\) . Ta có :
\(\hept{\begin{cases}a^2+b^2=1\left(1\right)\\4ab+1=a-b\left(2\right)\end{cases}}\)
(2) <=> : \(a\left(4b-1\right)=-b-1\)
TH 1 : \(b=\frac{1}{4}\) ko t/m
TH 2 : \(b\ne\frac{1}{4}\) ; ta có : \(a=\frac{b+1}{1-4b}\)
Thay vào (1) được : \(\left(\frac{b+1}{1-4b}\right)^2+b^2=1\Leftrightarrow\left(b+1\right)^2+b^2\left(1-4b\right)^2=\left(1-4b\right)^2\)
\(\Leftrightarrow b^2+2b+1+b^2\left(16b^2-8b+1\right)=16b^2-8b+1\)
\(\Leftrightarrow16b^4-8b^3+2b^2+2b+1=16b^2-8b+1\)
\(\Leftrightarrow16b^4-8b^3-14b^2+10b=0\)
\(\Leftrightarrow8b^4-4b^3-7b^2+5b=0\)
\(\Leftrightarrow b\left(8b^3-4b^2-7b+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}b=0\\b=-1\end{cases}}\)
Với b = 0 ; suy ra : a = 1 ( t/m ) Suy ra L \(\hept{\begin{cases}sinx=1\\cosx=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{\pi}{2}+2k\pi\\x=\frac{\pi}{2}+k\pi\end{cases}}\Leftrightarrow x=\frac{\pi}{2}+2k\pi}\) ( k thuộc Z )
Với b = - 1 ; suy ra a = 0 ; làm tương tự
Ko chắc
Đặt \(sinx-cosx=t,t\in\left[-\sqrt{2},\sqrt{2}\right]\).
\(\Rightarrow t^2=\left(sinx-cosx\right)^2=sin^2x+cos^2x-sin2x=1-sin2x\)
\(\Leftrightarrow sin2x=1-t^2\)
Phương trình ban đầu tương đương với:
\(2\left(1-t^2\right)=t-1\)
\(\Leftrightarrow\orbr{\begin{cases}t=1\left(tm\right)\\t=-\frac{3}{2}\left(l\right)\end{cases}}\)
Với \(t=1\):
\(sinx-cosx=1\)
\(\Leftrightarrow\sqrt{2}sin\left(x-\frac{\pi}{4}\right)=1\)
\(\Leftrightarrow\orbr{\begin{cases}x-\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x-\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{cases}}\left(k\inℤ\right)\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=\pi+k2\pi\end{cases}}\left(k\inℤ\right)\)

Do ABCD là hình thang cân nên AD = BC, AC = BC, ˆD=ˆCD^=C^
Xét hai tam giác ADC và BCD, ta có: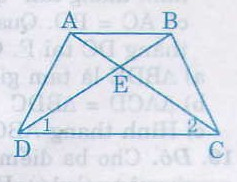
AD = BC (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra ˆC1=ˆD1C1^=D1^
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, ˆD=ˆCD^=C^ , DC là cạnh chung.

\(KL//MN\Rightarrow\widehat{K}+\widehat{N}=180^o\)
mà \(8\widehat{K}=\widehat{N}\)
suy ra \(\widehat{K}+8\widehat{K}=180^o\Leftrightarrow\widehat{K}=20^o\Rightarrow\widehat{N}=8.20^o=160^o\)


\(\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)^2=\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\)
\(\Leftrightarrow\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=\frac{a+b+c}{abc}=0\)
\(\Rightarrow a+b+c=0\)
Nếu cả ba số \(a,b,c\)đều là số lẻ thì \(a+b+c\)là số lẻ (mâu thuẫn vì \(a+b+c=0\)là số chẵn).
Do đó ít nhất một trong ba số \(a,b,c\)là số chẵn, do đó \(abc\)chia hết cho \(2\).
Ta có: \(a+b=-c\)
\(\Leftrightarrow\left(a+b\right)^3=-c^3\)
\(\Leftrightarrow a^3+b^3+3ab\left(a+b\right)=-c^3\)
\(\Leftrightarrow a^3+b^3+c^3=3abc⋮\left(abc\right)\)
Ta có đpcm.
A = (2n)^3−3n+1
⇔ A = (2n)^3−2n−n+1
⇔ A = 2n(n^2−1)−(n−1)
⇔ A = 2n(n−1)(n+1)−(n−1)
⇔ A = (2n^2+2n−1)(n−1)
Vì A là số nguyên tố nên n - 1 = 1
⇒ n = 2