ΔABC cân tại A

mà AD là đường trung tuyến

nên AD\(\perp\)BC

Xét ΔADB vuông tại D có DE là đường cao

nên \(DE\cdot AB=DA\cdot DB\)

\(\left(DE+AB\right)^2-\left(DA+DB\right)^2\)

\(=DE^2+AB^2+2\cdot DE\cdot AB-DA^2-DB^2-2\cdot DA\cdot DB\)

\(=DE^2+\left(AB^2-AB^2\right)=DE^2>0\)

=>\(\left(DE+AB\right)^2>\left(DA+DB\right)^2\)

=>DE+AB>DA+DB

Bài 1:

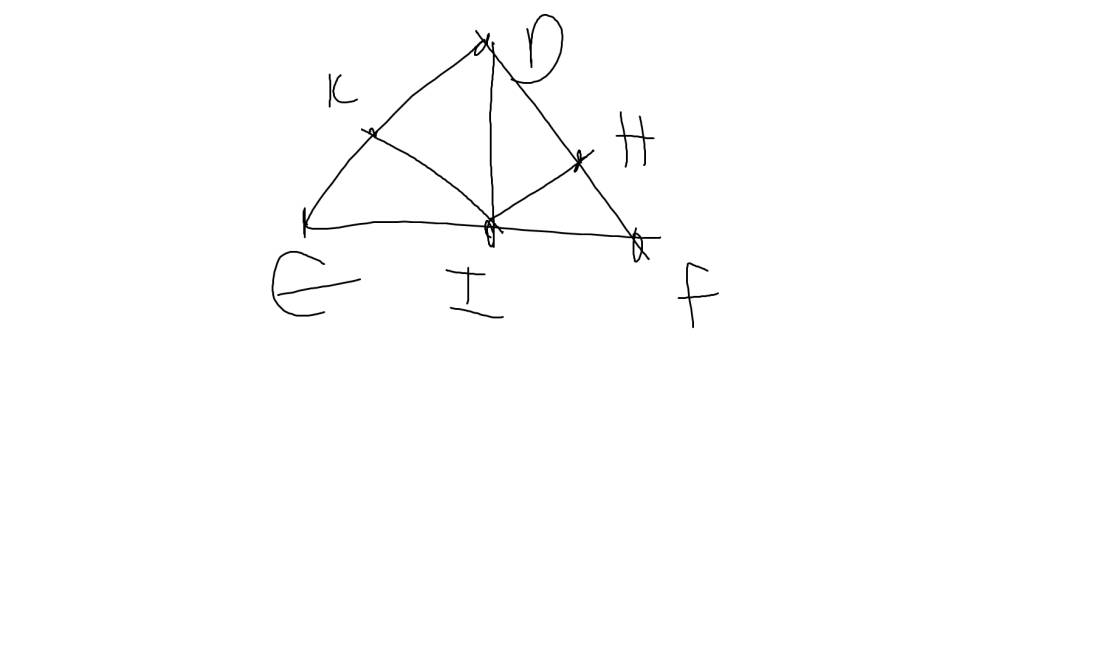
a: Xét ΔDEI và ΔDFI có

DE=DF

EI=FI

DI chung

Do đó: ΔDEI=ΔDFI

b: Ta có: ΔDEI=ΔDFI

=>\(\widehat{DIE}=\widehat{DIF}\)

mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)

nên \(\widehat{DIE}=\widehat{DIF}=\dfrac{180^0}{2}=90^0\)

=>DI\(\perp\)EF

ΔDEI=ΔDFI

=>\(\widehat{EDI}=\widehat{FDI}\)

=>DI là phân giác của góc EDF

c: Xét ΔIKE vuông tại K và ΔIHF vuông tại H có

IE=IF

\(\widehat{IEK}=\widehat{IFH}\)

Do đó: ΔIKE=ΔIHF

d: ta có: ΔIKE=ΔIHF

=>KE=HF và IK=IH

Ta có: DK+KE=DE

DH+HF=DF

mà DE=DF và KE=HF

nên DK=DH

=>D nằm trên đường trung trực của HK(1)

Ta có: IK=IH

=>I nằm trên đường trung trực của HK(2)

Từ (1),(2) suy ra DI là đường trung trực của HK

=>DI\(\perp\)HK

Xét ΔDEF có \(\dfrac{DK}{DE}=\dfrac{DH}{DF}\)

nên KH//EF

Bài 2:

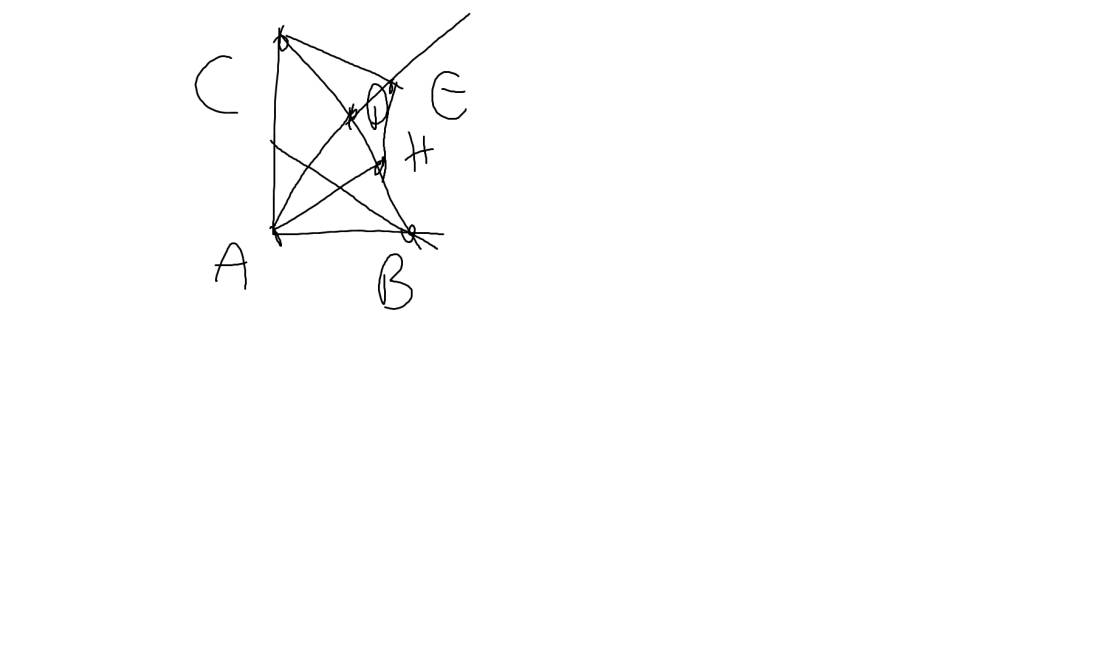
a: ΔABC vuông tại A

=>\(\widehat{ABC}+\widehat{ACB}=90^0\)

=>\(\widehat{ABC}=90^0-30^0=60^0\)

Xét ΔABD có

AH là đường cao

AH là đường trung tuyến

Do đó: ΔABD cân tại A

Xét ΔABD cân tại A có \(\widehat{ABD}=60^0\)

nên ΔABD đều

b: ΔABD đều

=>\(\widehat{BAD}=\widehat{BDA}=60^0\) và AB=BD=AD

\(\widehat{BAD}+\widehat{CAD}=\widehat{BAC}\)

=>\(\widehat{CAD}+60^0=90^0\)

=>\(\widehat{CAD}=30^0\)

Xét ΔDCA có \(\widehat{DCA}=\widehat{DAC}\)

nên ΔDAC cân tại D

=>DA=DC

c: Xét ΔDEC vuông tại E và ΔDHA vuông tại H có

DC=DA

\(\widehat{EDC}=\widehat{HDA}\)

Do đó: ΔDEC=ΔDHA

=>AH=CE và DE=DH

d: Xét ΔDEH và ΔDAC có

\(\dfrac{DE}{DA}=\dfrac{DH}{DC}\)

\(\widehat{EDH}=\widehat{ADC}\)

Do đó: ΔDEH~ΔDAC

=>\(\widehat{DEH}=\widehat{DAC}\)

=>EH//AC

Ta có: S_xq HHCN = (Chiều dài + chiều rộng).2.chiều cao(cm²) => = (58 + 45).2.x(cm²)= 206x(cm²).

Bài 2:

a: Xét ΔABC vuông tại A và ΔADC vuông tại A có

AB=AD

AC chung

Do đó: ΔABC=ΔADC

b: ΔABC=ΔADC

=>CB=CD
=>ΔCBD cân tại C

c: BF cắt DE tại I

nên B,I,F thẳng hàng

Bài 1:

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có

BD chung

BA=BE

Do đó: ΔBAD=ΔBED

b:

Sửa đề: Chứng minh DA<DC

Ta có: ΔBAD=ΔBED

=>DA=DE
mà DE<DC

nên DA<DC

Gọi số cây lớp 7A,7B,7C trồng được lần lượt là a(cây),b(cây),c(cây)

(ĐK: \(a,b,c\in Z^+\))

Số cây trồng được tỉ lệ thuận với số học sinh nên ta có:

\(\dfrac{a}{30}=\dfrac{b}{32}=\dfrac{c}{33}\)

Lớp 7A trồng được ít hơn lớp 7C là 6 cây nên c-a=6

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{30}=\dfrac{b}{32}=\dfrac{c}{33}=\dfrac{c-a}{33-30}=\dfrac{6}{3}=2\)

=>\(a=30\cdot2=60;b=32\cdot2=64;c=33\cdot2=66\)

Vậy: số cây lớp 7A,7B,7C trồng được lần lượt là 60(cây),64(cây),66(cây)

Bài 10:

a: \(DN=NE=\dfrac{DE}{2}\)

\(DM=MF=\dfrac{DF}{2}\)

mà DE=DF

nên DN=NE=DM=MF

Xét ΔDEM và ΔDFN có

DE=DF

\(\widehat{EDM}\) chung

DM=DN

Do đó: ΔDEM=ΔDFN

=>ME=FN

b: Xét ΔNEF và ΔMFE có

NE=MF

FE chung
NF=ME

Do đó: ΔNEF=ΔMFE

=>\(\widehat{KFE}=\widehat{KEF}\)

=>KE=KF

c: Xét ΔDKE và ΔDKF có

DK chung

KE=KF

DE=DF

Do đó: ΔKDE=ΔKDF

=>\(\widehat{KDE}=\widehat{KDF}\)

=>DK là phân giác của góc EDF

d: Ta có: ΔDEF cân tại D

mà DK là đường phân giác

nên DK là đường trung trực của EF

=>DK\(\perp\)EF tại trung điểm H của EF

Bài 11:

a: Ta có: \(\widehat{DBM}=\widehat{ABC}\)(hai góc đối đỉnh)

\(\widehat{ECN}=\widehat{ACB}\)(hai góc đối đỉnh)

mà \(\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{DBM}=\widehat{ECN}\)

Xét ΔDMB vuông tại M và ΔENC vuông tại N có

BD=CE
\(\widehat{DBM}=\widehat{ECN}\)

Do đó: ΔDMB=ΔENC

=>DM=EN

b: Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)

\(\widehat{ACB}+\widehat{ACN}=180^0\)

mà \(\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{ABM}=\widehat{ACN}\)

Xét ΔABM và ΔACN có

AB=AC

\(\widehat{ABM}=\widehat{ACN}\)

BM=CN

Do đó: ΔABM=ΔACN

=>AM=AN

=>ΔAMN cân tại A

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

b: Xét ΔEAD và ΔECB có

EA=EC

\(\widehat{AED}=\widehat{CEB}\)(hai góc đối đỉnh)

ED=EB

Do đó: ΔEAD=ΔECB

=>\(\widehat{EAD}=\widehat{ECB}\)

=>AD//CB

c: Sửa đề: AP=CQ

Xét ΔEAP và ΔECQ có

EA=EC

\(\widehat{EAP}=\widehat{ECQ}\)(AP//CQ)

AP=CQ

Do đó: ΔEAP=ΔECQ

=>\(\widehat{AEP}=\widehat{CEQ}\)

=>\(\widehat{AEP}+\widehat{AEQ}=180^0\)

=>P,Q,E thẳng hàng

a: Xét ΔBAD và ΔBED có

BA=BE

\(\widehat{ABD}=\widehat{EBD}\)

BD chung

Do đó: ΔBAD=ΔBED

=>\(\widehat{BAD}=\widehat{BED}\)

=>\(\widehat{BED}=90^0\)

=>DE\(\perp\)BC

b: ΔBAD=ΔBED

=>DA=DE

Xét ΔADK vuông tại A và ΔEDC vuông tại E có

DA=DE

\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)

Do đó:ΔADK=ΔEDC

c: Ta có: ΔADK=ΔEDC

=>AK=EC

Ta có: BA+AK=BK

BE+EC=BC

mà BA=BE và AK=EC

nên BK=BC

=>ΔBKC cân tại B

d: Xét ΔBKC có

CA,KE là các đường cao

CA cắt KE tại D

Do đó: D là trực tâm của ΔBKC

=>BD\(\perp\)KC