3/1x2 + 3/2x3 + 3/3x4 + ..... 3/2021x2022
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tỉ số giữa số tiền của Tom và số tiền của Jerry là:
\(\dfrac{5}{6}:\dfrac{3}{4}=\dfrac{5}{6}\cdot\dfrac{4}{3}=\dfrac{20}{18}=\dfrac{10}{9}\)
Tổng số phần bằng nhau là 10+9=19(phần)
Số tiền của Tom là \(420:19\cdot10=\dfrac{4200}{19}\left(USD\right)\)
Số tiền của Jerry là: \(420:19\cdot9=\dfrac{3780}{19}\left(USD\right)\)

Do \(x;y;z\le1\Rightarrow x+y+z\le3\)
Đồng thời: \(\left\{{}\begin{matrix}\left(1-z\right)\left(1-x\right)\ge0\Rightarrow1+zx\ge x+z\\\left(1-x\right)\left(1-y\right)\ge0\Rightarrow1+xy\ge x+y\\\left(1-y\right)\left(1-z\right)\ge0\Rightarrow1+yz\ge y+z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}1+y+zx\ge x+y+z\\1+z+xy\ge x+y+z\\1+x+yz\ge x+y+z\end{matrix}\right.\)
\(\Rightarrow\dfrac{x}{1+y+zx}+\dfrac{y}{1+z+xy}+\dfrac{z}{1+x+yz}\le\dfrac{x}{x+y+z}+\dfrac{y}{x+y+z}+\dfrac{z}{x+y+z}\)
\(=\dfrac{x+y+z}{x+y+z}\le\dfrac{3}{x+y+z}\)
Dấu "=" xảy ra khi \(x=y=z=1\)

Gọi số học sinh nam và số học sinh nữ lần lượt là a(bạn),b(bạn)
(Điều kiện: \(a,b\in Z^+\))
Số học sinh nam bằng 20/17 số học sinh nữ nên \(\dfrac{a}{20}=\dfrac{b}{17}\)
Tổng số học sinh nam và 4 lần số học sinh nữ là 352 nên a+4b=352
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{20}=\dfrac{b}{17}=\dfrac{a+4b}{20+4\cdot17}=\dfrac{352}{88}=4\)
=>\(a=4\cdot20=80;b=4\cdot17=68\)
Vậy: số học sinh nam và số học sinh nữ lần lượt là 80 bạn và 68 bạn

Bài 1:
a: 9h45p-7h45p=2h
Sau 2h thì người thứ nhất đi được 2*10=20(km/h)
=>Độ dài còn lại là 68-20=48(km/h)
Tổng vận tốc hai xe là 10+14=24(km/h)
Hai người gặp nhau sau khi người thứ hai xuất phát được:
48:24=2(giờ)
Hai người gặp nhau lúc:
9h45p+2h=11h45p
b:
Thời gian người thứ nhất đi từ A đến chỗ gặp nhau là:
2+2=4(giờ)
Chỗ gặp nhau cách A:
\(4\cdot10=40\left(km\right)\)

\(\left(x-2\right).\left(x-2\right)+2024=\left(x-2\right)^2+2024\ge2024\forall x\in R\\ Vậy:min_{BT}=2024\Leftrightarrow x-2=0\Leftrightarrow x=2\)

\(A=\dfrac{\left|x-2022\right|+2024-1}{\left|x-2022\right|+2024}=1-\dfrac{1}{\left|x-2022\right|+2024}\)
Do \(\left|x-2022\right|\ge0;\forall x\Rightarrow\left|x-2022\right|+2024\ge2024\)
\(\Rightarrow-\dfrac{1}{\left|x-2022\right|+2024}\ge-\dfrac{1}{2024}\)
\(\Rightarrow A\ge1-\dfrac{1}{2024}=\dfrac{2023}{2024}\)
\(A_{min}=\dfrac{2023}{2024}\) khi \(x-2022=0\Rightarrow x=2022\)

Lời giải:
$\frac{3}{1\times 3}+\frac{3}{3\times 5}+\frac{3}{5\times 7}+....+\frac{3}{57\times 59}$
$=\frac{3}{2}(\frac{3-1}{1\times 3}+\frac{5-3}{3\times 5}+\frac{7-5}{5\times 7}+....+\frac{59-57}{57\times 59})$
$=\frac{3}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{57}-\frac{1}{59})$
$=\frac{3}{2}(1-\frac{1}{59})=\frac{87}{59}$
Sửa đề: \(\dfrac{3}{1.3}+\dfrac{3}{3.5}+...+\dfrac{3}{57.59}\)
\(=\dfrac{3}{2}\left(\dfrac{2}{1.3}+\dfrac{2}{3.5}+...+\dfrac{2}{57.59}\right)\)
\(=\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{57}-\dfrac{1}{59}\right)\)
\(=\dfrac{3}{2}.\left(1-\dfrac{1}{59}\right)\)
\(=\dfrac{3}{2}.\dfrac{58}{59}=\dfrac{87}{59}\)

Lời giải:
Gọi hai số lần lượt là $a,b$. Theo bài ra ta có:
$a+b=25$
$2a-3b=5$
$\Rightarrow 3(a+b)+(2a-3b)=25.3+5$
$\Rightarrow 5a=80$
$\Rightarrow a=80:5=16$
$b=25-16=9$
Vậy hai số cần tìm là $16$ và $9$

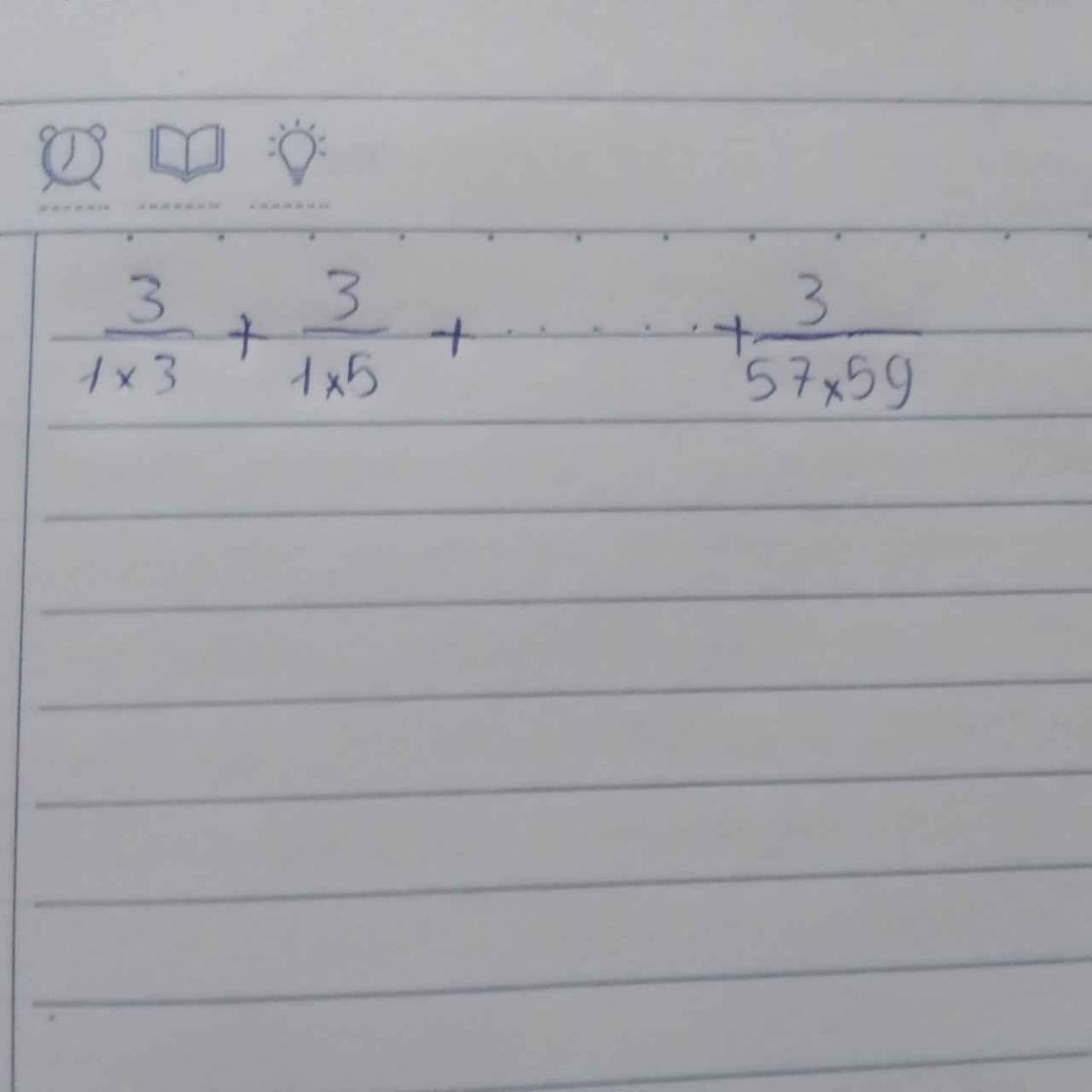
\(\dfrac{3}{1.2}+\dfrac{3}{2.3}+\dfrac{3}{3.4}+...+\dfrac{3}{2021.2022}\)
\(=3\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{2021.2022}\right)\)
\(=3.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\right)\)
\(=3.\left(1-\dfrac{1}{2022}\right)\)
\(=\dfrac{2021}{674}\)