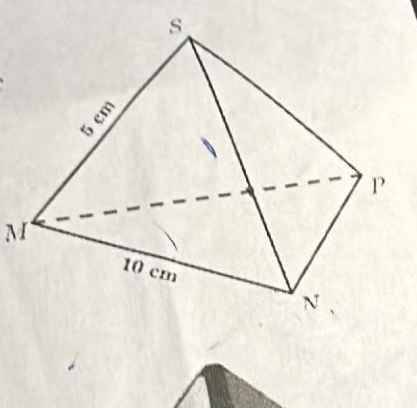
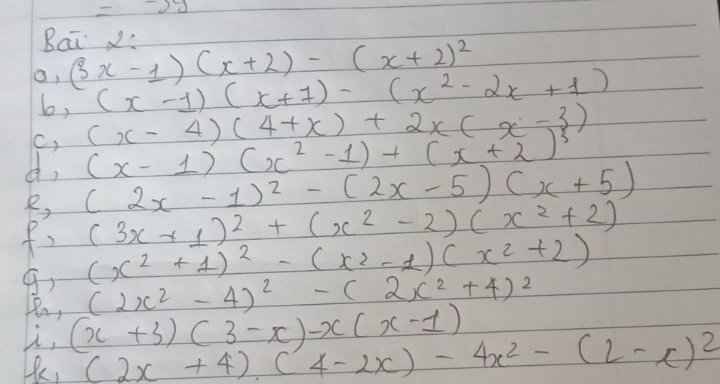Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: T= y-2x+4 với 36x2 +16y2 =9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=100^2-99^2+98^2-97^2+...+2^2-1^2\)
\(=\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\)
=100+99+98+97+...+2+1
\(=\dfrac{100\cdot101}{2}=50\cdot101=5050\)
\(A=100^2-99^2+98^2-97^2+...+2^2-1^2\\ =\left(100^2-99^2\right)+\left(98^2-97^2\right)+...+\left(2^2-1^2\right)\\ =\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+...+\left(2-1\right)\left(2+1\right)\\ =199+195+...+7+3\\ =\dfrac{\left[\left(199-3\right):4+1\right]\cdot\left(199+3\right)}{2}\\ =\dfrac{\left(196:4+1\right)\cdot202}{2}\\ =5050\)

ĐKXĐ: \(x\notin\left\{7;-1945\right\}\)
\(\dfrac{19x+8}{x-7}\cdot\dfrac{5x-9}{x+1945}+\dfrac{19x+8}{7-x}\cdot\dfrac{4x-2}{x+1945}\)
\(=\dfrac{19x+8}{x-7}\cdot\dfrac{5x-9}{x+1945}-\dfrac{19x+8}{x-7}\cdot\dfrac{4x-2}{x+1945}\)
\(=\dfrac{19x+8}{x-7}\cdot\dfrac{5x-9-4x+2}{x+1945}\)
\(=\dfrac{19x+8}{x+1945}\cdot\dfrac{x-7}{x-7}=\dfrac{19x+8}{x+1945}\)

a: Đề sai rồi bạn
b: Xét ΔIBK và ΔICN có
IB=IC
\(\widehat{BIK}=\widehat{CIN}\)(hai góc đối đỉnh)
IK=IN
Do đó: ΔIBK=ΔICN
=>BK=CN

\(4\left(x-2\right)-3\left(x+1\right)=5\)
\(\Leftrightarrow4x-8-3x-3=5\)
\(\Leftrightarrow\left(4x-3x\right)=5+8+3\)
\(\Leftrightarrow x=16\)
Vậy \(x=16\)

\(\text{Sửa đề }:x^4-3x+2=(x-1)(x^3+ax^2+bx-2)\\\Leftrightarrow x^4-x^3+x^3-x^2+x^2-x-2x+2=(x-1)(x^3+ax^2+bx-2)\\\Leftrightarrow x^3(x-1)+x^2(x-1)+x(x-1)-2(x-1)=(x-1)(x^3+ax^2+bx-2)\\\Leftrightarrow (x-1)(x^3+x^2+x-2)=(x-1)(x^3+ax^2+bx-2)\\\Rightarrow a=b=1\)

Bài 2:
Độ dài của `1/3` quãng đường đầu là:
`1/3*600=200` (km)
Thời gian xe đi trên `1/3` quãng đường đầu là:
\(\dfrac{200}{x}\left(h\right)\)
Quãng đường còn lại là: `600 - 200 = 400`(km)
Vận tốc của xe khi đi trên quãng đường còn lại: `x+10` (km/h)
Thời gian xe đi trên quãng đường còn lại là:
\(\dfrac{400}{x+10}\left(h\right)\)
Biểu thức thể hiện thời gian xe đi từ Hà Nội đến Quãng Ngãi là:
\(\dfrac{200}{x}+\dfrac{400}{x+10}=\dfrac{200\left(x+10\right)}{x\left(x+10\right)}+\dfrac{400x}{x\left(x+10\right)}=\dfrac{200x+2000+400x}{x\left(x+10\right)}=\dfrac{600x+2000}{x\left(x+10\right)}\)

a) \(x^2-36=0\)
\(\Leftrightarrow x^2-6^2=0\)
\(\Leftrightarrow\left(x-6\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-6=0\\x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
Vậy: ...
b) \(x^2-10x+25=0\)
\(\Leftrightarrow x^2-2\cdot x\cdot5+5^2=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
Vậy: ...
a) \(x^2-36=0\)
\(\Leftrightarrow x^2=36\)
\(\Leftrightarrow x^2=\left(\pm6\right)^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-6\end{matrix}\right.\)
Vậy \(x\in\left\{6;-6\right\}\)
b) \(x^2-10x+25=0\)
\(\Leftrightarrow x^2-2.x.5+5^2=0\)
\(\Leftrightarrow\left(x-5\right)^2=0\)
\(\Leftrightarrow x-5=0\)
\(\Leftrightarrow x=5\)
Vậy \(x=5\)

a) \(\left(3x-1\right)\left(x+2\right)-\left(x+2\right)^2\)
\(=\left(3x^2+6x-x-2\right)-\left(x+2\right)^2\)
\(=\left(3x^2+5x-2\right)-\left(x^2+4x+4\right)\)
\(=3x^2+5x-2-x^2-4x-4\)
\(=2x^2+x-6\)
b) \(\left(x-1\right)\left(x+1\right)-\left(x^2-2x+1\right)\)
\(=\left(x^2-1\right)-\left(x^2-2x+1\right)\)
\(=x^2-1-x^2+2x-1\)
\(=2x-2\)
c) \(\left(x-4\right)\left(4+x\right)+2x\left(x-3\right)\)
\(=\left(x-4\right)\left(x+4\right)+2x\left(x-3\right)\)
\(=\left(x^2-16\right)+2x^2-6x\)
\(=x^2-16+2x^2-6x\)
\(=3x^2-6x-16\)
d) \(\left(x-1\right)\left(x^2-1\right)+\left(x+2\right)^3\)
\(=\left(x^3-x-x^2+1\right)+\left(x^3+6x^2+12x+8\right)\)
\(=x^3-x-x^2+1+x^3+6x^2+12x+8\)
\(=2x^3+5x^2+11x+9\)
e) \(\left(2x-1\right)^2-\left(2x-5\right)\left(x+5\right)\)
\(=\left(4x^2-4x+1\right)-\left(2x^2+10x-5x-25\right)\)
\(=\left(4x^2-4x+1\right)-\left(2x^2+5x-25\right)\)
\(=4x^2-4x+1-2x^2-5x+25\)
\(=2x^2-9x+26\)
f) \(\left(3x+1\right)^2-\left(x^2-1\right)\left(x^2+2\right)\)
\(=\left(9x^2+6x+1\right)-\left(x^4+2x^2-x^2-2\right)\)
\(=\left(9x^2+6x+1\right)-\left(x^4+x^2-2\right)\)
\(=9x^2+6x+1-x^4-x^2+2\)
\(=-x^4+8x^2+6x+3\)
g) \(\left(x^2+1\right)^2-\left(x^2-1\right)\left(x^2+2\right)\)
\(=\left(x^4+2x^2+1\right)-\left(x^4+2x^2-x^2-2\right)\)
\(=\left(x^4+2x^2+1\right)-\left(x^4+x^2-2\right)\)
\(=x^4+2x^2+1-x^4-x^2+2\)
\(=x^2+3\)
h) \(\left(2x^2-4\right)^2-\left(2x^2+4\right)^2\)
\(=\left(4x^4-16x^2+16\right)-\left(4x^4+16x^2+16\right)\)
\(=4x^4-16x^2+16-4x^4-16x^2-16\)
\(=-32x^2\)