TK

B1: Đặt 3 quả táo nằm cạnh nhau

B2: Xác định đường thẳng nằm ngang chia đôi các quả táo

B3: Tiếp tục xác định đường thằng chia đôi một nửa các quả táo, dựa trên đường thẳng xác định ở bước 2

B4: Cắt ngang đường đã xác định ở bước 3

Để Na có thể cắt 3 quả táo thành 4 phần mà mỗi phần chỉ cần cắt một lần, cô ấy có thể thực hiện như sau:

1. Cắt một quả táo đầu tiên theo chiều dọc thành hai phần

2. Sau đó, cô ấy cắt một trong hai nửa đó theo chiều ngang, tạo ra hai phần nhỏ hơn (tổng cộng cô ấy đã cắt 3 quả táo thành 4 phần)

Như vậy, Na đã cắt 3 quả táo thành 4 phần một cách hiệu quả để phục vụ bố, mẹ, ông và bà.

?? Chx hiểu

???là sao bạn ơi

Phải có ảnh chứ bạn nhỉ !!!

ko ạ

B. không

thêm cũng được mà không thêm cũng được

Gọi chiều dài và chiều rộng hình chữ nhật đó lần lượt là a, b

Vì chu vi hình chữ nhật gấp 8 lần chiều rộng nên ta có:

`(a+b)\times 2=8\times b`

`a\times 2+b\times 2=8\times b`

`a\times 2=8\times b -b\times 2`

`a\times 2=b\times(8-2)`

`a\times 2=b\times 6`

$a=\frac{b\times 6}{2}=b\times 3$

hay chiều dài gấp 3 lần chiều rộng

Nếu ta coi chiều rộng của hình chữ nhật là 1 phần, thì chu vi của hình chữ nhật sẽ là 8 phần như thế.

Do chu vi của hình chữ nhật gấp 2 lần tổng chiều dài và chiều rộng nên tổng chiều dài và chiều rộng chiếm số phần là

$8:2=4$ (phần)

Mà chiều rộng chỉ có 1 phần nên chiều dài có số phần là

$4-1=3$ (phần)

Do chiều dài có 3 phần, chiều rộng có 1 phần nên chiều dài gấp chiều rộng số lần là

$3:1=3$ (lần)

Đáp số: 3 lần

đề đúng ko bạn ?

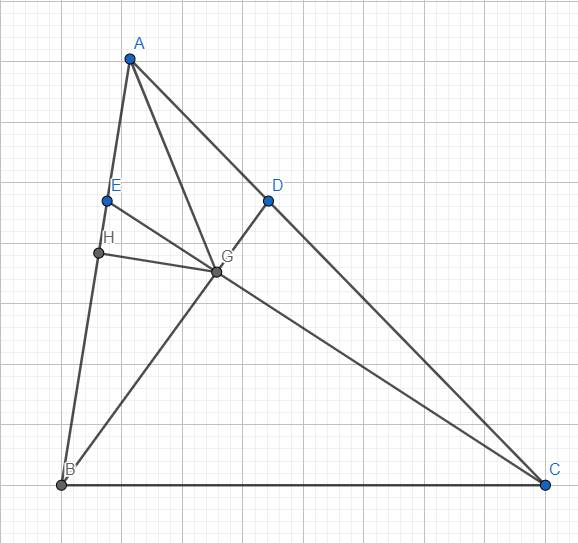
Gọi GH là đường cao của △BGE

Ta có: \(S_{BGE}=\dfrac{BE\times GH}{2}=10cm^2\)

Mà \(AE=2EB\Rightarrow BE=\dfrac{2}{3}AB\) nên:

\(\dfrac{\dfrac{2}{3}AB\times GH}{2}=10cm^2\)

\(\Rightarrow S_{AGB}=\dfrac{AB\times GH}{2}=15cm^2\)

    Đây là toán nâng cao chuyên đề lập số theo điều kiện cho trước, cấu trúc thi chuyên, thi học sinh giỏi các cấp, thi violympic. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng phương pháp giải ngược như sau:

                                           Giải:

+ Vì bỏ chữ số hàng chục của số đó ta được số mới kém số cần tìm 750 đơn vị nên số cần tìm phải lớn hơn 750 đơn vị. Vậy chữ số hàng trăm phải là 8.

Vậy số cần tìm chỉ có thể là: 836 hoặc 863

+ Nếu số cần tìm là 836 thì khi bỏ chữ số hàng chục ta được số mới là 86 khi đó theo bài ra ta có:

             836 - 86 = 750 (thỏa mãn)

+ Nếu số cần tìm là 863 thì khi bỏ chữ số hàng chục ta được số mới là 83 khi đó theo bài ra ta có:

           863 - 83 = 780 > 750 (không thỏa mãn)

Từ những lập luận và phân tích trên ta có số cần tìm là: 836

Đáp số: 836 

Olm chào em, Số chẵn bên tay phải và số lẻ ở bên tay trái em nhé. 

SỐ LẺ VÀ SỐ CHẴN EM CHƯA PHÂN BIỆT ĐƯỢC Ạ

đáp án E=MC ²

Công thức E=mc2E = mc^2E=mc2 là phương trình nổi tiếng của nhà vật lý học Albert Einstein. Phương trình này là một phần của thuyết tương đối hẹp và diễn tả mối quan hệ giữa năng lượng (E), khối lượng (m), và tốc độ ánh sáng trong chân không (c). Cụ thể:

• $E$ là năng lượng.
• $m$ là khối lượng.
• $c$ là tốc độ ánh sáng trong chân không, xấp xỉ 3×1083 \times 10^83×108 mét/giây.

Phương trình này cho thấy rằng khối lượng và năng lượng có thể hoán đổi cho nhau, nghĩa là một vật có khối lượng nhỏ cũng có thể chứa một lượng năng lượng khổng lồ. Điều này đã có những ứng dụng quan trọng trong nhiều lĩnh vực của vật lý, bao gồm cả việc giải thích năng lượng giải phóng trong phản ứng hạt nhân.

Albert Einstein đã công bố thuyết tương đối hẹp vào năm 1905 trong bài báo mang tên "Zur Elektrodynamik bewegter Körper" (Về điện động lực học của các vật chuyển động). Phương trình nổi tiếng E=mc2E = mc^2E=mc2 xuất hiện trong một bài báo tiếp theo vào năm 1905 với tiêu đề "Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?" (Sự quán tính của một vật có phụ thuộc vào năng lượng của nó không?).