`3x^2 + 4x - 4 = 0`

`<=> 3x^2 - 2x + 6x - 4 = 0`

`<=> (3x^2 - 2x) + (6x - 4) = 0`

`<=> x (3x - 2) + 2(3x - 2) = 0`

`<=> (x + 2)(3x - 2) = 0`

`<=> x = -2` hoặc `x = 2/3`

Vậy ...

\(x\) = \(-4+8\) / \(6\) = 2/3

Bài 17:

a:

Xét tứ giác OBAC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên OBAC là tứ giác nội tiếp

=>O,B,A,C cùng thuộc một đường tròn

Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

Ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC tại H và H là trung điểm của BC

Xét (O) có

ΔBCD nội tiếp

BD là đường kính

Do đó: ΔBCD vuông tại C

=>BC\(\perp\)CD
mà OA\(\perp\)BC

nên OA//CD

b: Xét (O) có

ΔBED nội tiếp

BD là đường kính

Do đó: ΔBED vuông tại E

=>BE\(\perp\)AD tại E

Xét ΔABD vuông tại B có BE là đường cao

nên \(AE\cdot AD=AB^2\left(3\right)\)

Xét ΔABO vuông tại B có BH là đường cao

nên \(AH\cdot AO=AB^2\left(4\right)\)

Từ (3),(4) suy ra \(AE\cdot AD=AH\cdot AO\)

=>\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)

Xét ΔAEH và ΔAOD có

\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)

\(\widehat{EAH}\) chung

Do đó: ΔAEH~ΔAOD

=>\(\widehat{AHE}=\widehat{ADO}\)

Bài 15:

a:

Xét (O) có

ΔBEC nội tiếp

BC là đường kính

Do đó: ΔBEC vuông tại E

=>BE\(\perp\)AC tại E

b: 

Xét (O) có

ΔBFC nội tiếp

BC là đường kính

Do đó: ΔBFC vuông tại F

=>CF\(\perp\)AB tại F

Xét ΔABC có

BE,CF là các đường cao

BE cắt CF tại H

Do đó: H là trực tâm của ΔABC

=>AH\(\perp\)BC tại D

Xét tứ giác BFHD có \(\widehat{BFH}+\widehat{BDH}=90^0+90^0=180^0\)

nên BFHD là tứ giác nội tiếp

Xét tứ giác CEHD có \(\widehat{CEH}+\widehat{CDH}=90^0+90^0=180^0\)

nên CEHD là tứ giác nội tiếp

Ta có: \(\widehat{FDH}=\widehat{FBH}\)(BFHD nội tiếp)

\(\widehat{EDH}=\widehat{ECH}\)(CEHD nội tiếp)

mà \(\widehat{FBH}=\widehat{ECH}\left(=90^0-\widehat{BAC}\right)\)

nên \(\widehat{FDH}=\widehat{EDH}\)

=>DA là phân giác của góc FDE

help me

a: Các kết quả có thể xảy ra nằm trong tập hợp sau:

\(\Omega=\left\{\left(1;1\right);\left(1;2\right);...;\left(6;5\right);\left(6;6\right)\right\}\)

=>Có 36 kết quả có thể xảy ra

b: Gọi A là biến cố "Tổng số chấm ở hai con xúc sắc là 7"

=>A={(1;6);(2;5);(3;4);(4;3);(5;2);(6;1)}

=>n(A)=6

=>\(P_A=\dfrac{6}{36}=\dfrac{1}{6}\)

a) Xúc xắc 1 có 6 kết quả (6 mặt)

Xúc xắc 2 có 6 kết quả

Số kết quả xảy ra khi tung 2 xúc xắc là: 

`6 xx 6 = 36` (kết quả) 

`69^2022`

`= (...9)^2022`

Có cùng chữ số tận cùng với `9^2022`

Ta có: `9^2022 = 9^(1011.2) = (9^2)^1011 = 81^1011` có tận cùng chữ số 1

Vậy ....

\(15^{15^{15^{15}}}\) có tận cùng là chữ số 5 do các chữ số tận cùng là 5 mũ bao nhiêu cũng tận cùng là 5 ngoại từ mũ 0

Để phương trình là phương trình bậc hai thì \(\sqrt{m}>=0\)

=>m>=0

Để phương trình có hai nghiệm phân biệt thì \(\left[-2\left(\sqrt{m}+1\right)\right]^2-4\left(\sqrt{m}+1\right)>0\)

=>\(4\left(m+2\sqrt{m}+1\right)-4\left(\sqrt{m}+1\right)>0\)

=>\(4\left(m+\sqrt{m}\right)>0\)(luôn đúng khi m>=0)

Điều kiện: `m >= 0`

Phương trình đã cho có 2 nghiệm phân biệt 

`<=> Δ' > 0`

`<=> (sqrt{m} + 1)^2 - (sqrt{m} + 1).1 > 0`

`<=> m^2 + 2sqrt{m} + 1 - sqrt{m} - 1 > 0`

`<=> m^2 + sqrt{m} >= 0` (Thỏa mãn với mọi `m >= 0)`

biểu đồ của em là :

Bài 1:

a: vẽ đồ thị:

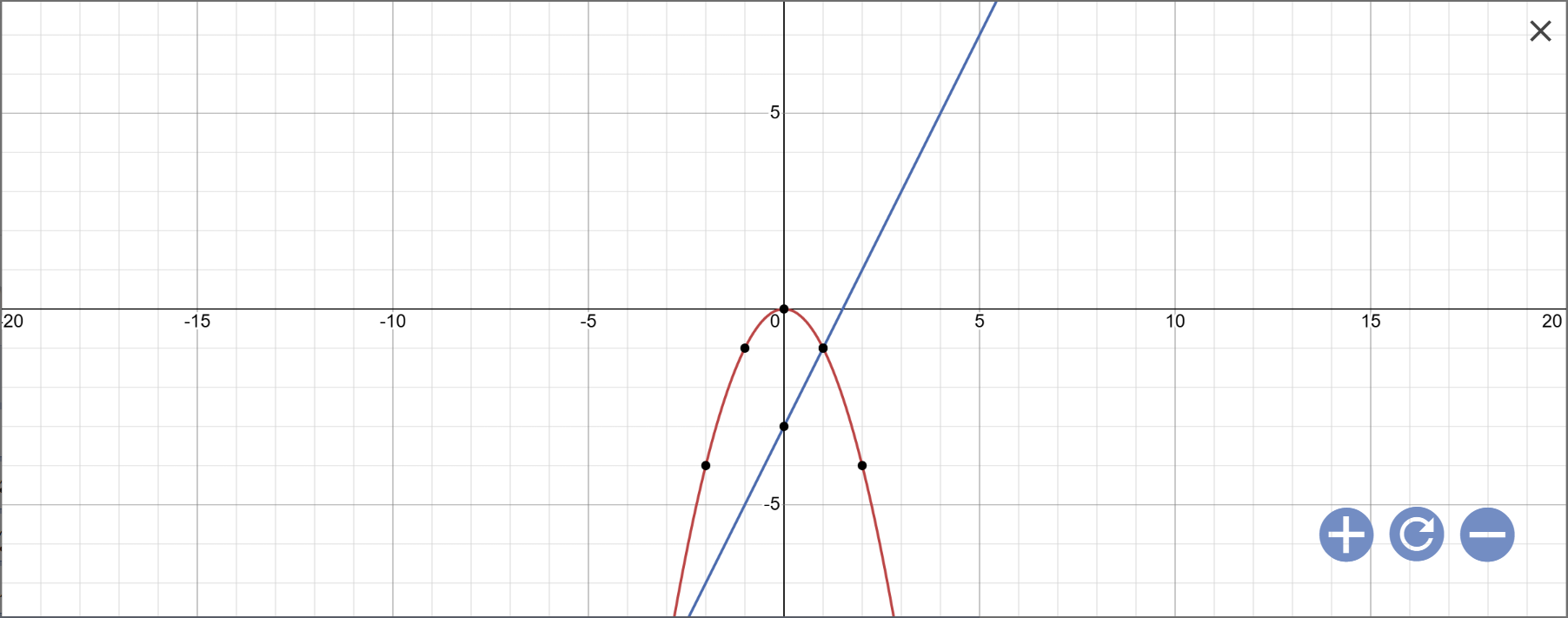
b: Phương trình hoành độ giao điểm là:

\(-x^2=2x-3\)

=>\(x^2+2x-3=0\)

=>(x+3)(x-1)=0

=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)

Khi x=-3 thì \(y=-x^2=-\left(-3\right)^2=-9\)

Khi x=1 thì \(y=-1^2=-1\)

Vậy: (P) cắt (d) tại A(-3;-9); B(1;-1)

Bài 2:

Phương trình hoành độ giao điểm là:

\(x^2=2x+8\)

=>\(x^2-2x-8=0\)

=>(x-4)(x+2)=0

=>\(\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)

Khi x=4 thì \(y=x^2=4^2=16\)

Khi x=-2 thì \(y=\left(-2\right)^2=4\)

Vậy: Tọa độ giao điểm là C(4;16); D(-2;4)

Bài 3:

Phương trình hoành độ giao điểm là:

\(3x^2=2x+1\)

=>\(3x^2-2x-1=0\)

=>\(3x^2-3x+x-1=0\)

=>(x-1)(3x+1)=0

=>\(\left[{}\begin{matrix}x-1=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{1}{3}\end{matrix}\right.\)

Khi x=1 thì \(y=3\cdot1^2=3\)

Khi x=-1/3 thì \(y=3\cdot\left(-\dfrac{1}{3}\right)^2=\dfrac{1}{3}\)

vậy: Tọa độ giao điểm là A(1;3); B(-1/3;1/3)

Bài 4:

a: Vẽ đồ thị: 

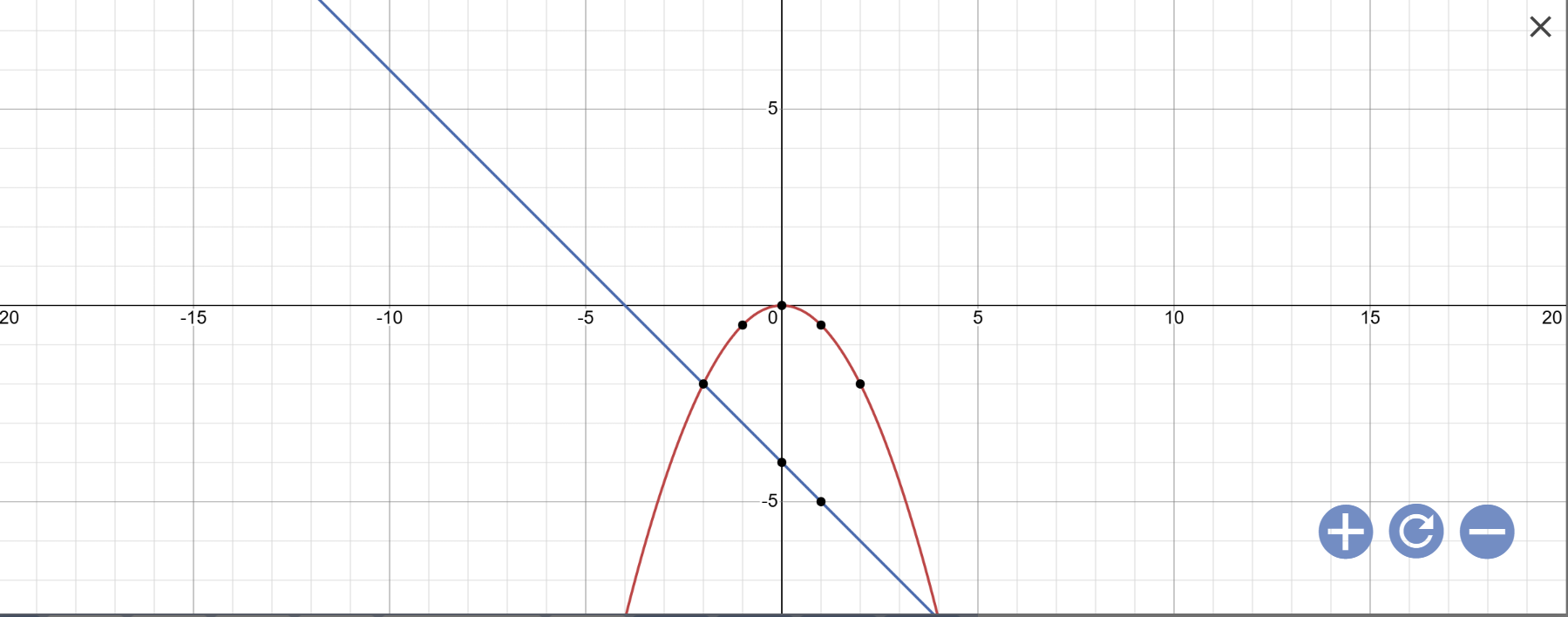
b: Phương trình hoành độ giao điểm là:

\(-\dfrac{x^2}{2}=-x-4\)

=>\(x^2=2x+8\)

=>\(x^2-2x-8=0\)

=>(x-4)(x+2)=0

=>\(\left[{}\begin{matrix}x-4=0\\x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)

Khi x=4 thì \(y=-x-4=-4-4=-8\)

Khi x=-2 thì y=-x-4=-(-2)-4=2-4=-2

Vậy: (P) cắt (d) tại A(4;-8); B(-2;-2)

Bài 5:

a: Vẽ đồ thị

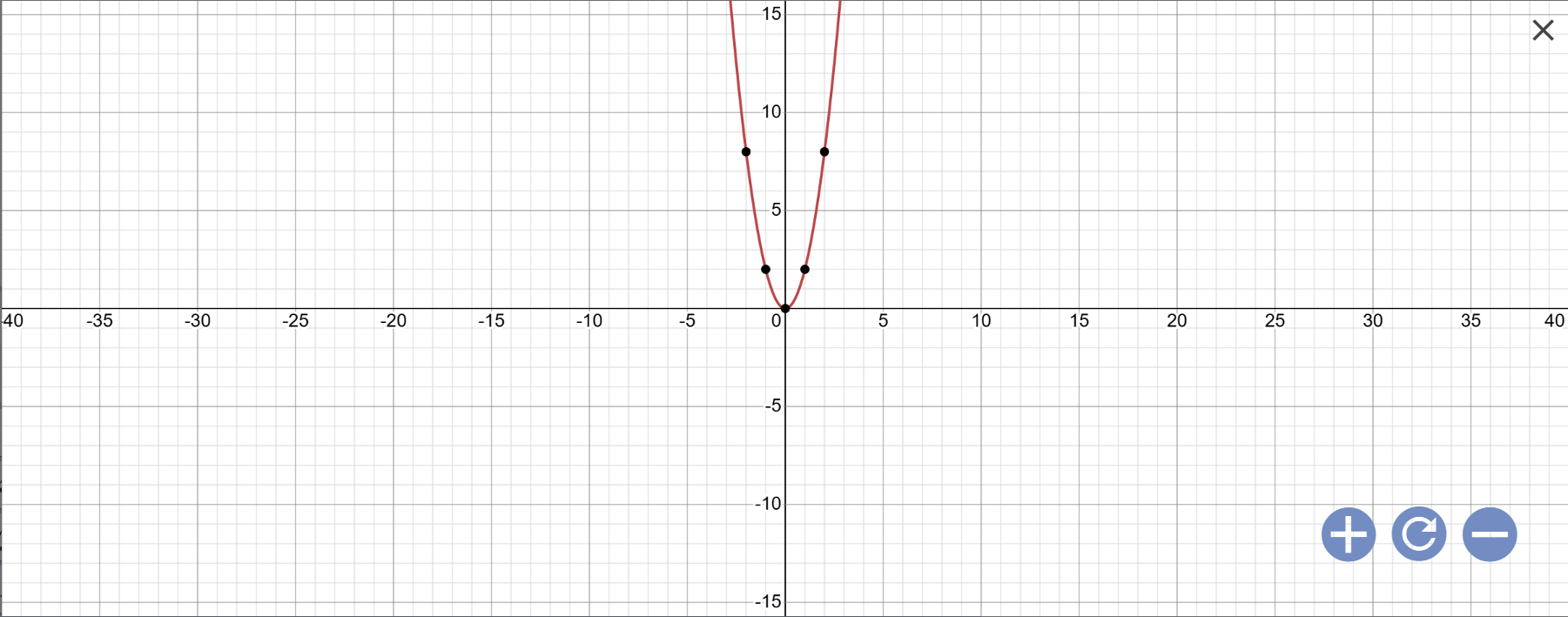
b: Phương trình hoành độ giao điểm là:

\(2x^2=5x-3\)

=>\(2x^2-5x+3=0\)

=>\(2x^2-2x-3x+3=0\)

=>(x-1)(2x-3)=0

=>\(\left[{}\begin{matrix}x-1=0\\2x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{2}\end{matrix}\right.\)

Khi x=1 thì \(y=2\cdot1^2=2\)

Khi x=3/2 thì \(y=2\cdot\left(\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)

Vậy: (d) cắt (P) tại A(1;2); \(B\left(\dfrac{3}{2};\dfrac{9}{2}\right)\)

Olm chào em, em cần đăng đầy đủ nội dung câu hỏi đó lên trên n này thì thầy cô mới có thể giải thích cho em tại sao lại có dòng:

- 4 x 1 x 2 em nhé.