
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=\dfrac{-\left(x^2+1\right)+2x^2-8x+8}{x^2+1}=-1+\dfrac{2\left(x-2\right)^2}{x^2+1}\ge-1\)
\(P_{min}=-1\) khi \(x-2=0\Rightarrow x=2\)
\(P=\dfrac{9\left(x^2+1\right)-8x^2-8x-2}{x^2+1}=9-\dfrac{2\left(2x+1\right)^2}{x^2+1}\le9\)
\(P_{max}=9\) khi \(2x+1=0\Rightarrow x=-\dfrac{1}{2}\)
\[
P = \frac{x^2 - 8x + 7}{x^2 + 1}
\]
\[
x^2 - 8x + 7 = (x^2 - 8x + 16) - 9 = (x-4)^2 - 9
\]
\[
P = \frac{(x-4)^2 - 9}{x^2 + 1}
\]
- Tại \( x = 0 \):
\[
P(0) = \frac{0^2 - 8 \times 0 + 7}{0^2 + 1} = \frac{7}{1} = 7
\]
- Tại \( x = 1 \):
\[
P(1) = \frac{1^2 - 8 \times 1 + 7}{1^2 + 1} = \frac{1 - 8 + 7}{2} = \frac{0}{2} = 0
\]
- Tại \( x = 2 \):
\[
P(2) = \frac{2^2 - 8 \times 2 + 7}{2^2 + 1} = \frac{4 - 16 + 7}{4 + 1} = \frac{-5}{5} = -1
\]
- Tại \( x = 4 \)
\[
P(4) = \frac{4^2 - 8 \times 4 + 7}{4^2 + 1} = \frac{16 - 32 + 7}{16 + 1} = \frac{-9}{17}
\]
- Tại \( x = -1 \):
\[
P(-1) = \frac{(-1)^2 - 8 \times (-1) + 7}{(-1)^2 + 1} = \frac{1 + 8 + 7}{1 + 1} = \frac{16}{2} = 8
\]
Dựa trên các giá trị đã tính, ta thấy rằng giá trị lớn nhất của \( P \) là \( 8 \) và giá trị nhỏ nhất là \( -1 \).
=> Max = 8
Min = -1

\(E=x^2-2xy+3y^2-2x-10y+20\\
=\left(x^2+y^2+1-2xy-2x+2y\right)+\left(2y^2-12y+72\right)-53\\
=\left(-x+y+1\right)^2+2\left(y-6\right)^2-53\)
Ta có:
`(-x+y+1)^2>=0` với mọi x,y
`2(y-6)^2>=0` với mọi y
`=>E=(-x+y+1)^2+2(y-6)^2-53>=-53` với mọi x,y
Dấu "=" xảy ra: `-x+y+1=0` và `y-6=0`
`<=>-x+7=0` và `y=6`
`<=>x=7` và `y=6`

\(D=\left(x^2-2xy+y^2\right)-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y\right)^2-12\left(x-y\right)+36+5y^2+9\)
\(=\left(x-y-6\right)^2+5y^2+9\)
Do \(\left\{{}\begin{matrix}\left(x-y-6\right)^2\ge0\\5y^2\ge0\end{matrix}\right.\) ;\(\forall x;y\)
\(\Rightarrow D\ge9\)
\(D_{min}=9\) khi \(\left\{{}\begin{matrix}x-y-6=0\\5y^2=0\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(6;0\right)\)

Ta có:
`14a + 21b + 5a - 2b`
`= (14a + 5a)+(21b - 2b)`
`= 19a + 19b`
`= 19. (a + b)`
`= 19 . 100`
`= 1900`
Vậy: `14a + 21b + 5a - 2b = 1900` với `a+b=100`

a: Xét ΔAHD vuông tại H và ΔDCB vuông tại C có
\(\widehat{ADH}=\widehat{DBC}\)(hai góc so le trong, AD//BC)
Do đó: ΔAHD~ΔDCB
b: Xét ΔBHA vuông tại H và ΔBAD vuông tại A có
\(\widehat{HBA}\) chung
DO đó ΔBHA~ΔBAD
=>\(\dfrac{BH}{BA}=\dfrac{BA}{BD}\)
=>\(BH\cdot BD=BA^2\)
c: ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(BH\cdot BD=BA^2\)
=>\(BH=\dfrac{3^2}{5}=1,8\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH=\sqrt{3^2-1,8^2}=2,4\left(cm\right)\)

\(1,M+N\\ =\left(2x^2-4xy+6y^2\right)+\left(2x^2+2xy-4y^2\right)\\ =2x^2-4xy+6y^2+2x^2+2xy-4y^2\\ =\left(2x^2+2x^2\right)+\left(-4xy+2xy\right)+\left(6y^2-4y^2\right)\\ =4x^2-2xy+2y^2\\ 2,M+\left(x^3-2xy^2+y^3\right)=x^3+5xy^2-y^3\\ =>M=\left(x^3+5xy^2-y^3\right)-\left(x^3-2xy^2+y^3\right)\\ =>M=x^3+5xy^2-y^3-x^3+2xy^2-y^3\\ =>M=\left(x^3-x^3\right)+\left(5xy^2+2xy^2\right)+\left(-y^3-y^3\right)\\ =>M=7xy^2-2y^3\)
1)
M + N = (2x² - 4xy + 6y²) + (2x² + 2xy - 4y²)
= 2x² - 4xy + 6y² + 2x² + 2xy - 4y²
= (2x² + 2x²) + (-4xy + 2xy) + (6y² - 4y²)
= 4x² - 2xy + 2y²
2)
M + (x³ - 2xy² + y³) = x³ + 5xy² - y³
M = x³ + 5xy² - y³ - (x³ - 2xy² + y³)
= x³ + 5xy² - y³ - x³ + 2xy² - y³
= (x³ - x³) + (5xy² + 2xy²) + (-y³ - y³)
= 7xy² - 2y³

\(a,2025-\left(2023-2022\right)^{2024}+\left(2024+1\right)^0\\ =2025-1^{2024}+2025^0\\ =2025-1+1\\ =2025\\ b,?\)
Nhìn đề câu b không hiểu bạn
`a, 2025 - (2023 - 2022)^2024+(2024+1)^0`
`= 2025 - 1^2024 + 2025^0`
`= 2025 - 1 +1`
`= 2024+1`
`=2025`
`b, (2^7)/13 . 3/(2^7)+ (2^10)/14 . 1/(2^6)`
`= 13/3+ (2^6 . 2^4)/14 . 1/(2^6)`
`= 13/3 + (2^4)/14`
`=13/3 + 16/14`
`= 115/21`

a, Diện tích xung quanh bể cá dạng hình hộp chữ nhật là:
\(2\cdot\left(4+5\right)\cdot10=180\left(cm^2\right)\)
Diện tích toàn phần bể cá dạng hình hộp chữ nhật là:
\(180+2\cdot4\cdot5=220\left(cm^2\right)\)
Thể tích bể cá dạng hình hộp chữ nhật là:
\(4\cdot5\cdot10=200\left(cm^3\right)\)
b, Diện tích xung quanh khi đổ nước vào bể cao 8 cm là:
\(2\cdot\left(4+5\right)\cdot8=144\left(cm^2\right)\)
Diện tích toàn phần khi đổ nước vào bể cao 8 cm là:
\(144+2\cdot4\cdot5=184\left(cm^2\right)\)
Thể tích khi đổ nước vào bể cao 8 cm là:
\(4\cdot5\cdot8=160\left(cm^3\right)\)
c, Thể tích phần không chứa nước là:
\(200-160=40\left(cm^2\right)\)
d, Tổng thể tích sau khi bỏ đá là:
\(160+100=260\left(cm^3\right)\)
Nước tràn ra ngoài là:
\(260-200=60\left(cm^3\right)\)
a) Diện tích xung quanh của bể cá là:
\(\left(4+5\right)\times2\times10=180\left(cm^2\right)\)
Diện tích toàn phần của bể cá là:
\(180+2\times4\times5=220\left(cm^2\right)\)
Thể tích của bể là:
\(4\times5\times10=200\left(cm^3\right)\)
b) Diện tích xung quanh:
\(\left(4+5\right)\times2\times8=144\left(cm^2\right)\)
Diện tích toàn phần:
\(144+2\times4\times5=184\left(cm^2\right)\)
Thể tích của nước có trong bể:
\(4\times5\times8=160\left(cm^3\right)\)
c) Diện tích phần không có nước là:
`200-160=40(cm^3)`
d) Khi bỏ cục đá vào thì thể tích của nước và cục đá là:
\(100+160=260\left(cm^2\right)\)
Vì: `260>200`
`=>` Nước bị tràn ra ngoài
Thể tích nước bị tràn là:
`260-200=60(cm^3)`

\(A=2+2^2+...+2^{100}\\ 2A=2^2+2^3+...+2^{101}\\ 2A-A=\left(2^2+2^3+...+2^{101}\right)-\left(2+2^2+...+2^{100}\right)\\ A=2^{101}-2\\ B=6^0+6^1+6^2+...+6^{1000}\\ 6B=6+6^2+...+6^{1001}\\ 6B-B=\left(6+6^2+...+6^{1001}\right)-\left(1+6+...+6^{1000}\right)\\ 5B=6^{1001}-1\\ B=\dfrac{6^{1001}-1}{5}\\ C=3+3^3+3^5+...+3^{101}\\ 3^2C=3^3+3^5+3^7+...+3^{103}\\ 9C-C=\left(3^3+3^5+3^7+...+3^{103}\right)-\left(3+3^3+3^5+...+3^{101}\right)\\ 8C=3^{103}-3\\ C=\dfrac{3^{103}-3}{8}\)
\(D=5+5^2+5^4+...+5^{98}\\ 5^2D=5^3+5^4+5^6+...+5^{100}\\ 25D-D=\left(5^3+5^4+5^6+....+5^{100}\right)-\left(5+5^2+5^4+...+5^{98}\right)\\ 24D=5^{100}+5^3-5-5^2\\ 24D=5^{100}+125-5-25\\ 24D=5^{100}+95\\ D=\dfrac{5^{100}+95}{24}\\ E=3^0+3^3+3^6+...+3^{96}+3^{99}\\ E=1+3^3+...+3^{99}\\ 3^3E=3^3+3^6+...+3^{102}\\ 27E-E=\left(3^3+3^6+...+3^{102}\right)-\left(1+3^3+...+3^{99}\right)\\ 26E=3^{102}-1\\ E=\dfrac{3^{102}-1}{6}\)
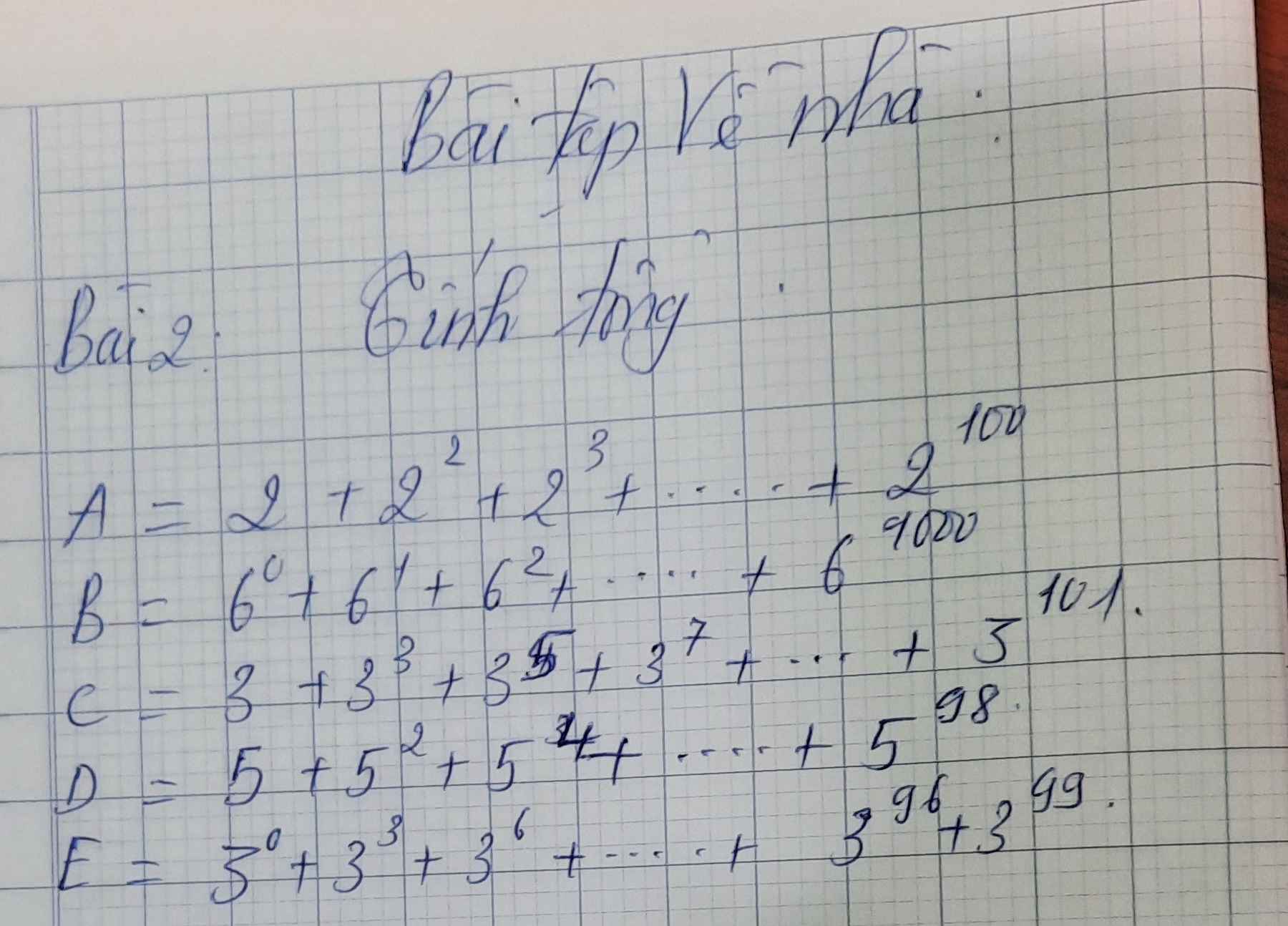
2)
\(a,8,2\times3,5+115+3,5\times1,8\\ =\left(8,2\times3,5+3,5\times1,8\right)+115\\ =3,5\times\left(8,2+1,8\right)+115\\ =3,5\times10+115\\ =35+115\\ =150\\ b,0,125\times0,12\times25\times1,7\times8\\ =\left(0,125\times8\right)\times\left(0,12\times25\right)\times1,7\\ =1\times3\times1,7\\ =3\times1,7\\ =5,1\)
Bài 1:
a: \(\left(57,17+8,63\right)\times9,5-98,44:2,3\)
=65,8x9,5-42,8
=625,1-42,8=582,3
b: \(61,35-8,6\times7,2:4,8+52,45\)
=61,35+52,45-12,9
=113,8-12,9=100,9