15

Số đó là: 15 

Vì khi ta thêm số 0 vào 15 thì ta được 105. Mà 105:15=7

Vậy số đó là:15

Ta có  1h = 60p 

    Do đó 4h 15p = 60x4 + 15 = 255 phút 

 2h 35p = 60x 2 + 35 = 155 phút 

Vậy 4h15p - 2h35p = 255 - 155 = 100 phút 

                                                    = 1h 40p

 Đ/s : 1h40 p

100

8 giờ tối = 20 giờ

Từ 5 giờ sáng đến 8 giờ tối có:

20 giờ - 5 giờ = 15 (giờ)

Mỗi giờ sớm 3 phút nên lúc 8 giờ tối đồng hồ chỉ:

8 giờ + 3 × 15 phút = 8 giờ 45 phút

a.

$=\frac{10-8xy^3+12xy^3+10}{4x^3y^2}=\frac{20+4xy^3}{4x^3y^2}$

$=\frac{5+xy^3}{x^3y^2}$
b.

$=\frac{4(x-2)+2(x+2)}{(x+2)(x-2)}+\frac{6-5x}{(x-2)(x+2)}$

$=\frac{6x-4}{(x+2)(x-2)}+\frac{6-5x}{(x-2)(x+2)}$

$=\frac{x+2}{(x-2)(x+2)}=\frac{1}{x-2}$
c.

$=\frac{4x+7-(3x+6)}{2x+2}=\frac{x+1}{2(x+1)}=\frac{1}{2}$

d.

$=\frac{y+6}{(y-2)(y+2)}-\frac{2}{y(y+2)}$

$=\frac{y(y+6)-2(y-2)}{y(y+2)(y-2)}=\frac{y^2+4y+4}{y(y+2)(y-2)}=\frac{(y+2)^2}{y(y+2)(y-2)}=\frac{y+2}{y(y-2)}$

e.

$=\frac{4y+7}{3y+2}.\frac{3y+2}{8y+14}=\frac{4y+7}{8y+14}=\frac{4y+7}{2(4y+7)}=\frac{1}{2}$
g.

$=\frac{3y+2}{4(2y+3)}.\frac{2y+3}{3y+2}=\frac{1}{4}$

h.

$=\frac{2y+3}{y+3}.\frac{3(y+3)}{2y+3}=3$

Lời giải:

a. $=\frac{6xy^2.3y}{6xy^2.4x^2}=\frac{3y}{4x^2}$

b.

$=\frac{(x-y)(x^2+xy+y^2)}{(x-y)(x+y)}=\frac{x^2+xy+y^2}{x+y}$

c.

$=\frac{5(4x^2-9)}{(2x+3)^2}=\frac{5(2x-3)(2x+3)}{(2x+3)^2}=\frac{5(2x-3)}{2x+3}$
d.

$=\frac{4x(x^2+2x+1)}{2x^2(x+1)}=\frac{4x(x+1)^2}{2x^2(x+1)}=\frac{2(x+1)}{x}$

Lời giải:

a. Bạn tự vẽ hình

b. PT hoành độ giao điểm của $(d), (d')$:

$x+2=-2x+8\Leftrightaarrow 3x=6\Leftrightarrow x=2$

$y=x+2=2+2=4$

Vậy $A$ có tọa độ $(2,4)$

$B\in Ox$ nên $y_B=0$

$B\in (d)$ nên $y_B=x_B+2\Rightarrow x_B=y_B-2=0-2=-2$
Vậy $B(-2,0)$
$C\in Ox$ nên $y_C=0$

$C\in (d')$ nên $y_C=-2x_C+8\Rightarrow x_C=\frac{y_C-8}{-2}=\frac{-8}{-2}=4$

Vậy $C(4,0)$

Diện tích tam giác $ABC$:

$S_{ABC}=\frac{d(A,BC).BC}{2}=\frac{d(A,Ox).BC}{2}=\frac{|y_A|(|x_B|+|x_C|)}{2}=\frac{4(2+4)}{2}=12$ (đvdt)

Dài quá bạn ơi

160

640 : 4 = 160

a.

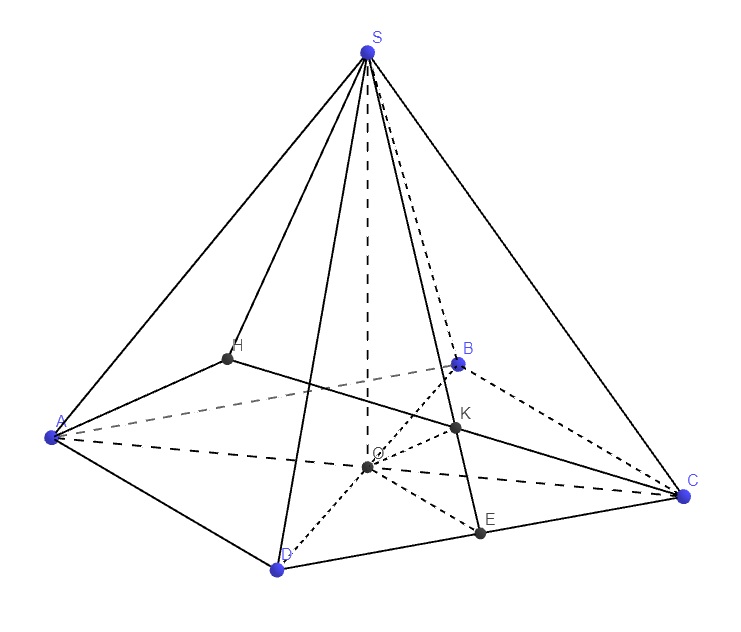
Do chóp S.ABCD đều \(\Rightarrow SO\perp\left(ABCD\right)\)

\(\Rightarrow\) O là hình chiếu vuông góc của S lên (ABCD)

\(\Rightarrow\Delta OAB\) là hình chiếu vuông góc của \(\Delta SAB\) lên (ABCD)

b.

Gọi E là trung điểm CD \(\Rightarrow OE\) là đường trung bình tam giác BCD

\(\Rightarrow OE||BC\Rightarrow OE\perp CD\)

\(\Rightarrow CD\perp\left(SOE\right)\)

Trong mp (SOE), từ O kẻ \(OK\perp SE\)

\(OK\in\left(SOE\right)\Rightarrow CD\perp OK\)

\(\Rightarrow OK\perp\left(SCD\right)\)

Trong mp (ACK), qua A kẻ đường thẳng song song OK cắt CK kéo dài tại H

\(\Rightarrow AH\perp\left(SCD\right)\Rightarrow SH\) là hình chiếu vuông góc của SA lên (SCD)

\(\Rightarrow\widehat{ASH}\) là góc giữa SA và (SCD) hay \(\widehat{ASH}=\varphi\)

\(OE=\dfrac{1}{2}BC=\dfrac{a}{2}\) 

Áp dụng hệ thức lượng trong tam giác vuông SOE:

\(OK=\dfrac{SO.OE}{\sqrt{SO^2+OE^2}}=\dfrac{a\sqrt{5}}{5}\)

O là trung điểm AC và \(OK||SH\Rightarrow OK\) là đường trung bình tam giác CAH

\(\Rightarrow AH=2OK=\dfrac{2a\sqrt{5}}{5}\)

\(OA=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\Rightarrow SA=\sqrt{SO^2+OA^2}=\dfrac{a\sqrt{6}}{2}\)

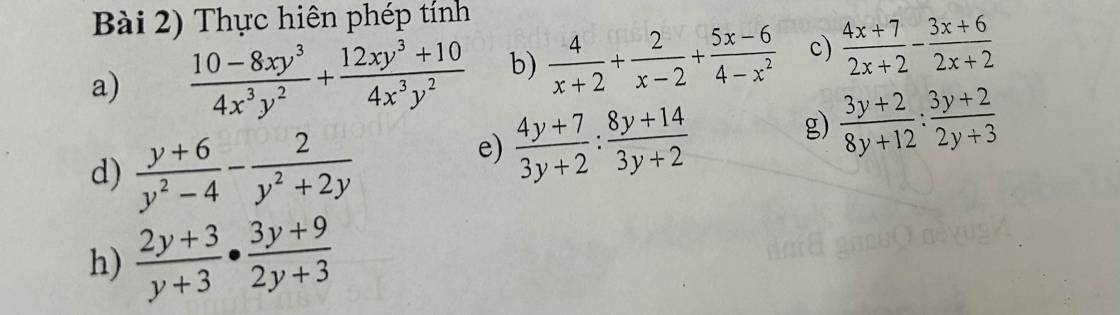
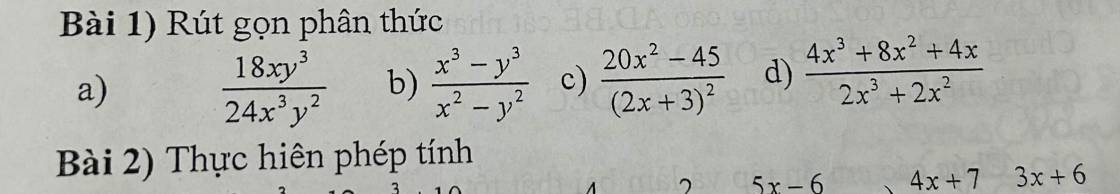
\(\Rightarrow sin\varphi=\dfrac{AH}{SA}=\dfrac{2\sqrt{30}}{15}\)