Tính giá trị biểu thức hợp lí:
\(\dfrac{2^{19}.27^3+15.2^{18}.3^8}{9^4.4^{10}+12^{10}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

48÷1×5=240(con gà)
Vậy lúc đầu bác An mang 240 con gà ra chợ bán

\(4987m^2=49dam^287m^2\)
\(320060dam^2=32km^26000m^2\)
3,2 yến=32kg
36dm=3,6m
5,4 tấn=5400kg
148dm=1480cm
1,2kg=1200g
204m=2040dm
1/5 tạ=20kg

2m16cm=216cm
Nửa chu vi tấm vải là 618:2=309(cm)
Chiều rộng tấm vải là 309-216=93(cm)
Đổi 2m16cm=216cm
Chiều rộng tấm vải là:
(618÷2)-216=93(cm)
Đ/s: 93cm

Thời gian còn lại để Minh đạp xe đến trường là:
7h-6h30p-10p=20p=1/3(giờ)
vận tốc Minh cần đi để đến trường đúng giờ là:
\(2,5:\dfrac{1}{3}=7,5\left(\dfrac{km}{h}\right)\)

a: Xét ΔBDE vuông tại E và ΔBCD vuông tại D có
\(\widehat{DBE}\) chung
Do đó: ΔBDE~ΔBCD
b: Xét ΔBFD vuông tại F và ΔBDA vuông tại D có
\(\widehat{FBD}\) chung
Do đó: ΔBFD~ΔBDA
=>\(\dfrac{BF}{BD}=\dfrac{BD}{BA}\)
=>\(BD^2=BF\cdot BA\)
c: Ta có: ΔBDE~ΔBCD
=>\(\dfrac{BD}{BC}=\dfrac{BE}{BD}\)
=>\(BD^2=BE\cdot BC\)
=>\(BF\cdot BA=BE\cdot BC\)
=>\(\dfrac{BF}{BC}=\dfrac{BE}{BA}\)
Xét ΔBFE và ΔBCA có
\(\dfrac{BF}{BC}=\dfrac{BE}{BA}\)
\(\widehat{FBE}\) chung
Do đó: ΔBFE~ΔBCA
=>\(\widehat{BFE}=\widehat{BCA}\)
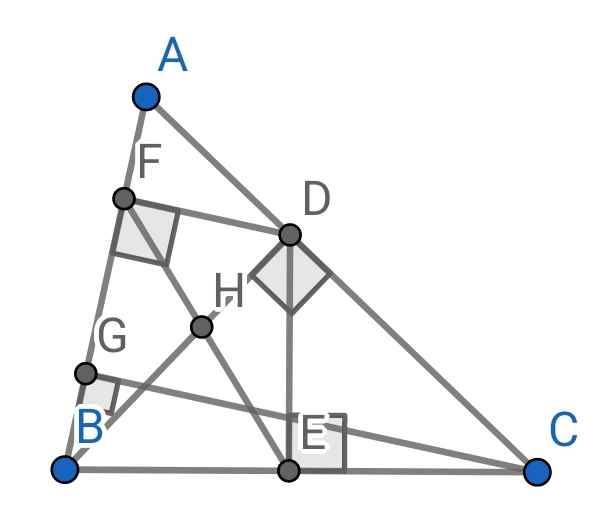
a) Xét hai tam giác vuông: ∆BDE và ∆BCD có:
∠B chung
⇒ ∆BDE ∽ ∆BCD (g-g)
b) Xét hai tam giác vuông: ∆BFD và ∆BDA có:
∠B chung
⇒ ∆BFD ∽ ∆BDA (g-g)
⇒ BF/BD = BD/BA
⇒ BD² = BF.BA
c) Do ∆BDE ∽ ∆BCD (cmt)
⇒ BD/BC = BE/BD
⇒ BD² = BE.BC
Mà BD² = BF.BA (cmt)
⇒ BF.BA = BE.BC
⇒ BF/BC = BE/BA
Xét ∆BFE và ∆BCA có:
BA/BC = BE/BA (cmt)
∠B chung
⇒ ∆BFE ∽ ∆BCA (c-g-c)
d) Em xem lại đề, đề thiếu vì hình bị mất

1: Xét ΔCEH vuông tại E và ΔCAB vuông tại A có
\(\widehat{ECH}\) chung
Do đó: ΔCEH~ΔCAB
2: Xét tứ giác AHEB có \(\widehat{HAB}+\widehat{HEB}=90^0+90^0=180^0\)
nên AHEB là tứ giác nội tiếp
=>\(\widehat{HBC}=\widehat{EAC}\)
3:
Xét ΔIBA và ΔIEH có
\(\widehat{IBA}=\widehat{IEH}\)(ABEH là tứ giác nội tiếp)
\(\widehat{BIA}=\widehat{EIH}\)(hai góc đối đỉnh)
Do đó; ΔIBA~ΔIEH
=>\(\dfrac{AB}{EH}=\dfrac{AI}{HI}\)
=>\(AB\cdot HI=AI\cdot HE\)

\(\dfrac{2^{19}\cdot27^3+15\cdot4^9\cdot9^4}{9^4\cdot4^{10}+12^{10}}\)
=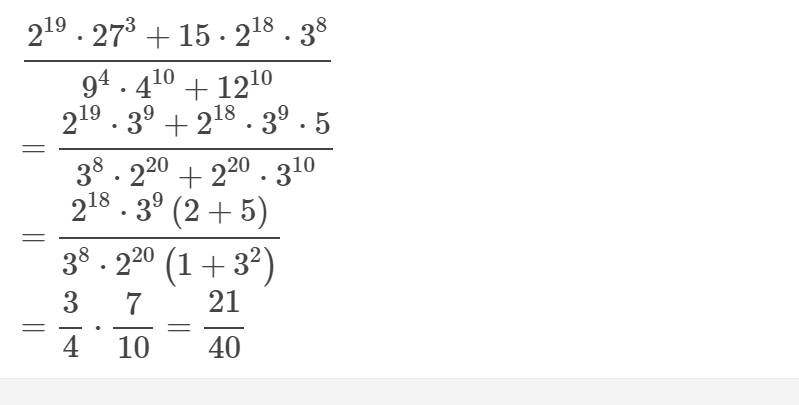

a: \(C=\left(\dfrac{2+x}{2-x}+\dfrac{4x^2}{4-x^2}-\dfrac{2-x}{2+x}\right):\dfrac{x^2-x}{2x-x^2}\)
\(=\left(\dfrac{-\left(x+2\right)}{x-2}-\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right)\cdot\dfrac{x\left(2-x\right)}{x\left(x-1\right)}\)
\(=\dfrac{-\left(x+2\right)^2-4x^2+\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{2-x}{x-1}\)
\(=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x+2\right)}\cdot\dfrac{-1}{x-1}\)
\(=\dfrac{-4x^2-8x}{\left(x+2\right)\left(x-1\right)}\cdot\left(-1\right)=\dfrac{4x\left(x+2\right)}{\left(x+2\right)\left(x-1\right)}=\dfrac{4x}{x-1}\)
b: Để C=1 thì 4x=x-1
=>3x=-1
=>\(x=-\dfrac{1}{3}\left(nhận\right)\)
c: Để C là số nguyên thì \(4x⋮x-1\)
=>\(4x-4+4⋮x-1\)
=>\(4⋮x-1\)
=>\(x-1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(x\in\left\{2;0;3;-1;5;-3\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{3;-1;5;-3\right\}\)

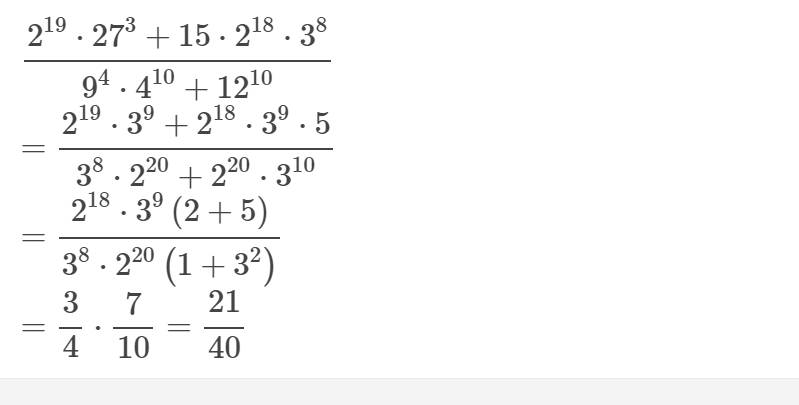

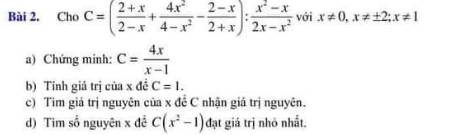
\(\dfrac{2^{19}\cdot27^3+15\cdot2^{18}\cdot3^8}{9^4\cdot4^{10}+12^{10}}\)
\(=\dfrac{2^{19}\cdot3^9+2^{18}\cdot3^9\cdot5}{3^8\cdot2^{20}+2^{20}\cdot3^{10}}\)
\(=\dfrac{2^{18}\cdot3^9\left(2+5\right)}{3^8\cdot2^{20}\left(1+3^2\right)}\)
\(=\dfrac{3}{4}\cdot\dfrac{7}{10}=\dfrac{21}{40}\)
Các bạn giúp mình với!