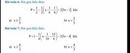Giải Dùm Mình Đi

n3−n2+2n+7n2+1=(n3+n)−(n2+1)+n+8n2+1=n(n2+1)−(n2+1)+n+8n2+1n3−n2+2n+7n2+1=(n3+n)−(n2+1)+n+8n2+1=n(n2+1)−(n2+1)+n+8n2+1

n−1+n+8n2+1n−1+n+8n2+1

Do n3−n2+2n+7⋮n2+1n3−n2+2n+7⋮n2+1 ⇒n3−n2+2n+7n2+1∈Z⇒n3−n2+2n+7n2+1∈Z

⇒n−1+n+8n2+1∈Z⇒n−1+n+8n2+1∈Z

⇒n=−8

đến n-1+\(\frac{n+8}{n^2+1}\)nguyên .=>(n+8)(n-8) chia hết cho n²+1 [vì n+8 luôn chia hết cho n²+1]

=>(n²-64) chia hết cho (n²+1) hay (n²+1-65) chia hết cho (n²+1) mà n²+1 >0 với mọi n nguyên

=>n²+1 thuộc Ư₍₆₅₎={5,13,1,65}

=>n thuộc {2,-2,0,8,-8} 

thử lại ta có : n=0 (thỏa mãn) .

n=-2 (ko thỏa mãn)

n=2 (thỏa mãn)

n=8 (ko thỏa mãn)

n=-8 (thỏa mãn)

vậy n thuộc {0;2;-8}

\(\frac{x}{-3}\)\(=\) \(\frac{y}{7}\)và \(x^2-y^2=160\)

Đặt : \(\frac{x}{-3}=\frac{y}{7}=k\)

\(\Rightarrow\hept{\begin{cases}x=-3k\\y=7k\end{cases}}\)

Thay vào : \(x^2-y^2=160\)ta được :

\(\left(-3k\right)^2-\left(7k\right)^2=160\)

\(\left(-3\right)^2.k^2-\left(7\right)^2.k^2=160\)

\(9.k^2-49.k^2=160\)

\(\left(9-49\right).k^2=160\)

\(-40.k=160\)

\(k=-4\)

Thay vào ta được :

\(\Rightarrow\hept{\begin{cases}x=-3.\left(-4\right)=12\\y=7.\left(-4\right)=-28\end{cases}}\)

Vậy ....................

$A\left(x\right)={\left(3-4+x^2\right)}^{2004}{\left(3+4x+x^2\right)}^{2005}$

Đa thức $A\left(x\right)$ sau khi bỏ dấu ngoặc:

$A\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+...+a_{1}x+a_0$

Với $n=2.2004+2.2005=8018$

Ta thay $x=1$ thì $A\left(1\right)=a_n+a_{n-1}+...+a_1+a_0$

$\Rightarrow A\left(1\right)$ là tổng các hệ số của $A\left(x\right)$ khi bỏ dấu ngoặc

Ta có: $A\left(1\right)={\left(3-4.1+1^2\right)}^{2004}{\left(3+4.1+1^2\right)}^{2005}$

$=0^{2004}{.8}^{2005}=0$

Vậy tổng các hệ số của đa thức $A\left(x\right)$ nhận được sau khi bỏ dấu ngoặc là $0$

\(a,2x^2-4x>0\)

=>  \(2x\left(x-2\right)>0\)

=> \(\orbr{\begin{cases}2x>0\\x-2>0\end{cases}\Leftrightarrow\orbr{\begin{cases}x>0\\x>2\end{cases}}}\)