Tìm n biết rằng: n3 - n2 + 2n + 7 chia hết cho n2 + 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A\left(x\right)=\left(3-4x+x^2\right)^{2004}\left(3+4x+x^2\right)^{2005}\)
Đa thức A(x) sau khi bỏ dấu ngoặc:
\(A\left(x\right)=a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0\)
Với n = 2 . 2004 + 2 . 2005 = 8018
Ta thay x=1 thì \(A\left(1\right)=a_n+a_{n-1}+a_1+a_0\)
⇒ A(1) là tổng các hệ số của A(x) khi bỏ dấu ngoặc
Ta có: \(A\left(1\right)=\left(3-4\cdot1+1^2\right)^{2004}\left(3+4\cdot1+1^2\right)^{2005}\)
\(=0^{2004}\cdot8^{2005}=0\)
Vậy tổng các hệ số của đa thức A(x) nhận được sau khi bỏ dấu ngoặc là 0

\(=\left(x-\frac{1}{3}\right)^2+1\)
\(=x^2-\frac{2}{3}x+\frac{1}{9}+1\)
\(=x^2-\frac{2}{3}x+\frac{10}{9}\)


Đáp án :
\(-3\notinℕ\)
\(-3\in Z\)
\(-3\in Q\)
\(\frac{-2}{3}\notin Z\)
\(\frac{-2}{3}\in Q\)
\(N\subset Z\subset Q\)
tả lời minh ko biết đánh kí hiệu nên là vậy nha
-3 ko thuộc N / -3 thuộc Z / -3 thuộc Q
-2/3 ko thuộc Q / -2/3 thuộc Q / N là tập hợp con của Z mà Z lại là tập hợp con của Q
chúc bn có 1 năm học mới vui vẻ

\(a)\)\(\left[\left(\frac{1}{9}\div\frac{8}{27}\right)\div-\frac{1}{3}\right]\div\frac{81}{128}\)
\(=\)\(\left[\left(\frac{1}{9}.\frac{27}{8}\right)\div-\frac{1}{3}\right]\div\frac{81}{128}\)
\(=\)\(\left[\frac{3}{8}\div-\frac{1}{3}\right]\div\frac{81}{128}\)
\(=\)\(\left[\frac{3}{8}.-3\right]\div\frac{81}{128}\)
\(=\)\(-\frac{9}{8}\div\frac{81}{128}\)
\(=\)\(-\frac{9}{8}.\frac{128}{81}\)
\(=\)\(-\frac{16}{9}\)
\(b)\)\(\left(-\frac{7}{15}\right).\frac{5}{8}.\left(\frac{15}{-7}\right).\left(-32\right)\)
\(=\)\(\frac{-7.5.15}{15.8.-7}.\left(-32\right)\)
\(=\)\(\frac{5}{8}.\left(-32\right)\)
\(=\)\(-20\)

Ta có : \(\frac{2020}{2021}=\frac{2020.2022}{2021.2022}=\frac{\left(2021-1\right)\left(2021+1\right)}{2021.2022}=\frac{2021^2-1}{2021.2022}\)
\(\frac{2021}{2022}=\frac{2021^2}{2021.2022}\)
Vì 20212 > 20212 - 1 nên \(\frac{2021^2-1}{2021.2022}< \frac{2021^2}{2021.2022}\)
Hay \(\frac{2020}{2021}< \frac{2021}{2022}\)

 ai giải được hết hộ mình chứng tả cần cù và mình tym cho nha
ai giải được hết hộ mình chứng tả cần cù và mình tym cho nha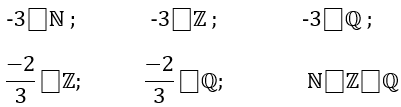
đến n - 1 + \(\frac{n+8}{n^2+1}\) nguyên .=>(n+8)(n-8) chia hết cho n2+1 [vì n+8 luôn chia hết cho n2+1]
=>(n2-64) chia hết cho (n2+1) hay (n2+1-65) chia hết cho (n2+1) mà n2+1 >0 với mọi n nguyên
=>n2+1 thuộc Ư(65)={5,13,1,65}
=>n thuộc {2,-2,0,8,-8}
thử lại ta có : n=0 (thỏa mãn) .
n=-2 (ko thỏa mãn)
n=2 (thỏa mãn)
n=8 (ko thỏa mãn)
n=-8 (thỏa mãn)
vậy n thuộc {0;2;-8}
\(\frac{n^3-n^2+2n+7}{n^2+1}=\frac{(n^3+n)-(n^2+1)+n+8}{n^2+1}=\frac{n(n^2+1)+n+8}{n^2+1}\)
\(n-1+\frac{n+8}{n^2+1}\)
Do \(n^3-n^2+2n+7⋮n^2+1\Rightarrow\frac{n^3-n^2+2n+7}{n^2+1}\)
\(n-1+\frac{n+8}{n^2+1}\)
\(\Rightarrow n=-8\)