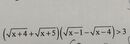Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.







\(D=[4;+\infty)\)
Bất phương trình tương đương:
\(\frac{\sqrt{x-4}-\sqrt{x-1}}{\sqrt{x+4}-\sqrt{x+5}}>3\)
\(\Leftrightarrow\sqrt{x-4}+3\sqrt{x+5}>3\sqrt{x+4}+\sqrt{x-1}\)
\(\Leftrightarrow10x+41+6\sqrt{x^2+x-20}>10x+35+6\sqrt{x^2+3x-4}\)(Vì VP và VT dương)
\(\Leftrightarrow1+\sqrt{x^2+x-20}>\sqrt{x^2+3x-4}\)
\(\Leftrightarrow1+2\sqrt{x^2+x-20}+x^2+x-20>x^2+3x-4\)(Vì \(VT>VP\ge0\))
\(\Leftrightarrow2\sqrt{x^2+x-20}>2x+15\)
\(\Leftrightarrow2x+15< 0\left(h\right)\hept{\begin{cases}2x+15\ge0\\4\left(x^2+x-20\right)>4x^2+60x+225\end{cases}}\)
\(\Leftrightarrow x< -\frac{15}{2}\left(h\right)\hept{\begin{cases}x\ge-\frac{15}{2}\\x< -\frac{305}{56}\end{cases}}\Leftrightarrow x< -\frac{305}{56}\)
Kết hợp TXĐ thì BPT vô nghiệm.