giúp mik với!!

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


AB//CD
=>\(y=\widehat{BDC}\)(hai góc so le trong)
=>\(y=45^0\)
AB//CD
=>\(x+100^0=180^0\)
=>\(x=80^0\)
\(x-y=80^0-45^0=35^0\)

xx'//yy'
=>\(\widehat{xAB}+\widehat{yBz}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{yBz}+70^0=180^0\)
=>\(\widehat{yBz}=110^0\)
xx'//yy'
=>\(\widehat{xAB}=\widehat{yBz'}\)(hai góc đồng vị)
=>\(\widehat{yBz'}=70^0\)

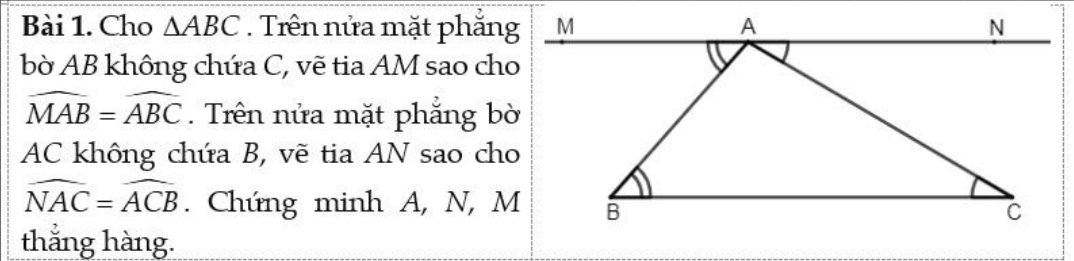
Ta có: \(\widehat{MAB}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên MA//BC
Ta có: \(\widehat{NAC}=\widehat{ACB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NA//BC
Ta có: MA//BC
NA//BC
MA,NA có điểm chung là A
Do đó: M,A,N thẳng hàng

a: \(\left(-\dfrac{2}{5}-\dfrac{4}{3}+\dfrac{1}{4}\right)-\left(\dfrac{3}{5}-\dfrac{1}{3}-\dfrac{3}{4}\right)\)
\(=-\dfrac{2}{5}-\dfrac{4}{3}+\dfrac{1}{4}-\dfrac{3}{5}+\dfrac{1}{3}+\dfrac{3}{4}\)
\(=\left(-\dfrac{2}{5}-\dfrac{3}{5}\right)+\left(-\dfrac{4}{3}+\dfrac{1}{3}\right)+\left(\dfrac{1}{4}+\dfrac{3}{4}\right)\)
=-1-1+1=-1
b: \(\dfrac{2}{5}-\left(\dfrac{4}{3}+\dfrac{4}{5}\right)-\left(-\dfrac{1}{9}-0,4\right)+\dfrac{11}{9}\)
\(=\dfrac{2}{5}-\dfrac{4}{3}-\dfrac{4}{5}+\dfrac{1}{9}+\dfrac{2}{5}+\dfrac{11}{9}\)
\(=\left(\dfrac{2}{5}-\dfrac{4}{5}+\dfrac{2}{5}\right)+\left(-\dfrac{4}{3}+\dfrac{1}{9}+\dfrac{11}{9}\right)\)
\(=0+\left(-\dfrac{4}{3}+\dfrac{12}{9}\right)=0\)
c: \(\dfrac{11}{8}\cdot\left[\left(-\dfrac{5}{11}:\dfrac{13}{8}-\dfrac{5}{11}:\dfrac{13}{5}\right)+\dfrac{-6}{33}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\cdot\dfrac{8}{13}-\dfrac{5}{11}\cdot\dfrac{5}{13}-\dfrac{2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left[-\dfrac{5}{11}\left(\dfrac{8}{13}+\dfrac{5}{13}\right)-\dfrac{2}{11}\right]+\dfrac{3}{4}\)
\(=\dfrac{11}{8}\cdot\left(-\dfrac{5}{11}-\dfrac{2}{11}\right)+\dfrac{3}{4}=\dfrac{-7}{8}+\dfrac{3}{4}=-\dfrac{1}{8}\)
d: \(A=\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{2}{3}\right)+\dfrac{4}{9}:\left(\dfrac{1}{11}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\left(\dfrac{1}{15}-\dfrac{10}{15}\right)+\dfrac{4}{9}:\left(\dfrac{2}{22}-\dfrac{5}{22}\right)\)
\(=\dfrac{4}{9}:\dfrac{-9}{15}+\dfrac{4}{9}:\dfrac{-3}{22}\)
\(=\dfrac{4}{9}\cdot\dfrac{-5}{3}+\dfrac{4}{9}\cdot\dfrac{-22}{3}=\dfrac{4}{9}\cdot\left(-\dfrac{5}{3}-\dfrac{22}{3}\right)=\dfrac{4}{9}\left(-9\right)=-4\)

a: Trên tia Ox, ta có: OM<ON
nên M nằm giữa O và N
=>OM+MN=ON
=>MN+4=8
=>MN=4(cm)
b: Ta có: M nằm giữa O và N
MN=MO(=4cm)
Do đó: M là trung điểm của ON
c: Trên tia Ox, ta có: OP<OM
nên P nằm giữa O và M
=>OP+PM=OM
=>PM+2=4
=>PM=2(cm)
Ta có: P nằm giữa O và M
mà OP=PM(=2cm)
nên P là trung điểm của OM
Trên tia Ox, ta có: OM<OQ
nên M nằm giữa O và Q
=>OM+MQ=OQ
=>MQ+4=6
=>MQ=2(cm)
Vì MP=MQ(=2cm)
nên M là trung điểm của PQ
Trên tia Ox, ta có: OQ<ON
nên Q nằm giữa O và N
=>OQ+QN=ON
=>QN+6=8
=>QN=2(cm)
Vì MQ=QN(=2cm)
nên Q là trung điểm của MN

a: Các cặp tia đối nhau gốc A là:
AB,Ax
AO,Ax
Ay,Ax
b: Trên tia Ay, ta có: AO<AB(3cm<6cm)
nên O nằm giữa A và B
=>AO+OB=AB
=>OB+3=6
=>OB=3(cm)
c: Vì O nằm giữa A và B
và OA=OB(=3cm)
nên O là trung điểm của AB
a) Cặp tia đối nhau gốc A trên hình vẽ là tia OA và tia AO.
b) Độ dài đoạn thẳng OB có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông OAB:
OB² = OA² + AB²
OB² = 3² + 6²
OB² = 9 + 36
OB² = 45
OB = √45 ≈ 6.71 cm
c) Điểm O không phải là trung điểm của đoạn thẳng AB. Để chứng minh điều này, ta có thể tính độ dài của OA và OB:
OA = 3 cm
OB = 6.71 cm
Ta thấy OA ≠ OB, do đó O không là trung điểm của AB.
tick mik nha

a: Trên tia AB, ta có: AC<AB
nên C nằm giữa A và B
=>AC+CB=AB
=>CB+1=4
=>CB=3(cm)
b: B là trung điểm của CD
=>\(CD=2\cdot CB=2\cdot3=6\left(cm\right)\)

Hình bạn tự vẽ nhé.
Ta có: \(ON+NM=OM\\ \Rightarrow3+MN=7\\ \Rightarrow MN=4cm\)
Mà \(A\) là trung điểm \(MN\)
\(\Rightarrow NA=AM=\dfrac{1}{2}MN\\ \Rightarrow NA=AM=2cm\)
Ta có: \(OA=ON+NA\\ \Rightarrow OA=3+2\\ \Rightarrow OA=5cm\)
Vậy...

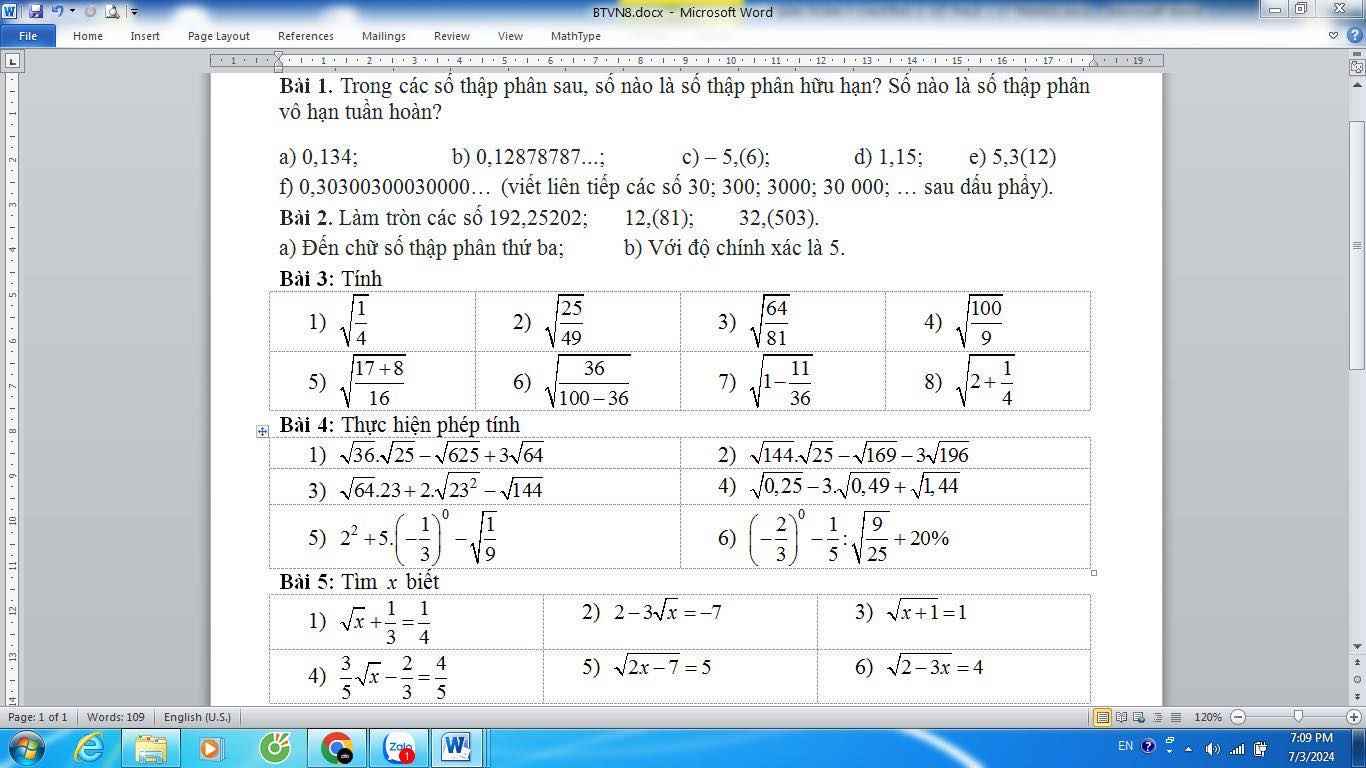
Câu 3:
1: \(\sqrt{\dfrac{1}{4}}=\dfrac{\sqrt{1}}{\sqrt{4}}=\dfrac{1}{2}\)
2: \(\sqrt{\dfrac{25}{49}}=\dfrac{\sqrt{25}}{\sqrt{49}}=\dfrac{5}{7}\)
3: \(\sqrt{\dfrac{64}{81}}=\dfrac{\sqrt{64}}{\sqrt{81}}=\dfrac{8}{9}\)
4: \(\sqrt{\dfrac{100}{9}}=\dfrac{\sqrt{100}}{\sqrt{9}}=\dfrac{10}{3}\)
5: \(\sqrt{\dfrac{17+8}{16}}=\sqrt{\dfrac{25}{16}}=\dfrac{\sqrt{25}}{\sqrt{16}}=\dfrac{5}{4}\)
6: \(\sqrt{\dfrac{36}{100-36}}=\sqrt{\dfrac{36}{64}}=\sqrt{\dfrac{9}{16}}=\dfrac{\sqrt{9}}{\sqrt{16}}=\dfrac{3}{4}\)
7: \(\sqrt{1-\dfrac{11}{36}}=\sqrt{\dfrac{36}{36}-\dfrac{11}{36}}=\sqrt{\dfrac{25}{36}}=\dfrac{\sqrt{25}}{\sqrt{36}}=\dfrac{5}{6}\)
8: \(\sqrt{2+\dfrac{1}{4}}=\sqrt{\dfrac{9}{4}}=\dfrac{\sqrt{9}}{\sqrt{4}}=\dfrac{3}{2}\)
Câu 5:
1: ĐKXĐ: x>=0
\(\sqrt{x}+\dfrac{1}{3}=\dfrac{1}{4}\)
=>\(\sqrt{x}=\dfrac{1}{4}-\dfrac{1}{3}=-\dfrac{1}{12}\)<0(vô lý)
=>Phương trình vô nghiệm
2: ĐKXĐ: x>=0
\(2-3\sqrt{x}=-7\)
=>\(3\sqrt{x}=2+7=9\)
=>\(\sqrt{x}=3\)
=>\(x=3^2=9\)(nhận)
3: ĐKXĐ: x+1>=0
=>x>=-1
\(\sqrt{x+1}=1\)
=>\(x+1=1^2=1\)
=>x=1-1=0(nhận)
4: ĐKXĐ: x>=0
\(\dfrac{3}{5}\sqrt{x}-\dfrac{2}{3}=\dfrac{4}{5}\)
=>\(\dfrac{3}{5}\sqrt{x}=\dfrac{2}{3}+\dfrac{4}{5}=\dfrac{10}{15}+\dfrac{12}{15}=\dfrac{22}{15}\)
=>\(\sqrt{x}=\dfrac{22}{15}:\dfrac{3}{5}=\dfrac{22}{15}\cdot\dfrac{5}{3}=\dfrac{110}{45}=\dfrac{22}{9}\)
=>\(x=\left(\dfrac{22}{9}\right)^2=\dfrac{264}{81}\)
5: ĐKXĐ: 2x-7>=0
=>x>=7/2
\(\sqrt{2x-7}=5\)
=>\(2x-7=5^2=25\)
=>2x=7+25=32
=>x=32/2=16(nhận)
6: ĐKXĐ: 2-3x>=0
=>3x<=2
=>\(x< =\dfrac{2}{3}\)
\(\sqrt{2-3x}=4\)
=>\(2-3x=4^2=16\)
=>3x=2-16=-14
=>\(x=-\dfrac{14}{3}\left(nhận\right)\)


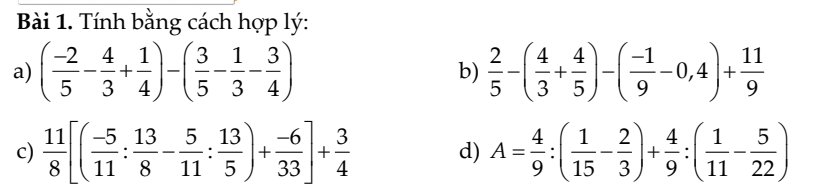
\(a.\dfrac{\dfrac{3}{4}-\dfrac{3}{5}+\dfrac{3}{7}+\dfrac{3}{13}}{\dfrac{11}{4}-\dfrac{11}{5}+\dfrac{11}{7}+\dfrac{11}{13}}:\dfrac{\dfrac{3}{5}-\dfrac{3}{8}+\dfrac{3}{11}}{\dfrac{7}{5}-\dfrac{7}{9}+\dfrac{7}{11}}\\ =\dfrac{3\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{11}\right)}{11\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{11}\right)}:\dfrac{3\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}{7\left(\dfrac{1}{5}-\dfrac{1}{9}+\dfrac{1}{11}\right)}\\ =\dfrac{3}{11}:\dfrac{3}{7}\\ =\dfrac{3}{11}\cdot\dfrac{7}{3}\\ =\dfrac{7}{11}\\ b.\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{19\cdot21}\\ =\dfrac{1}{2}\cdot\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{19\cdot21}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{19}-\dfrac{1}{21}\right)\\ =\dfrac{1}{2}\cdot\left(1-\dfrac{1}{21}\right)\\ =\dfrac{1}{2}\cdot\dfrac{20}{21}=\dfrac{10}{21}\)