tìm nghiệm của đa thức H(x)=3-x^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


35 x 4 : 1 + 100 : 35 : 6 : 5 + 34
= 140 : 1 + \(\frac{20}{7}\) : 6 : 5 + 34
= 140 + \(\frac{10}{21}\) : 5 + 34
= (140 + 34) + \(\frac{2}{21}\)
= 174 + \(\frac{2}{21}\)
= \(\frac{3654}{21}\) + \(\frac{2}{21}\)
= \(\frac{3656}{21}\)

a)
f(x)= -x5 -7x4 -2x3+ x2 + 4x + 8
g(x)=x5 +7x4+2x3+3x2 - 3x -8
f(x)+g(x) =0 -0 -0 + 4x2 +x+0
g(x)=x5 +7x4+2x3+3x2 - 3x -8
f(x)= -x5 -7x4 -2x3+ x2 + 4x + 8
g(x)-f(x) =2x5+14x4+4x3+2x2-7x -16
b)
Bậc:5
Hệ số cao nhất:2
hệ số tự do:16
c)
Để đt h(x) có nghiệm thì
4x2+x=0
->4x.x+x=0
->(4x+1)x=0
->th1:x=0 -> x=0
4x+1=0 -> x=-1/4
Vậy đt h(x) có nghiệm là x=0 hoặc x=-1/4
Lần sau bn viết rõ hơn nhé
mik dich mún lòi mắt

Giải:
Nếu y tỉ lệ nghịch với x theo tỉ lệ là a thì x cũng tỉ lệ với y theo hệ số tỉ lệ là a

a: Bảng tần số:
| Cân nặng | 28 | 30 | 31 | 32 | 36 | 45 | |
| Số bạn | 3 | 3 | 5 | 6 | 2 | 1 | N=20 |
Tần số tương ứng của giá trị 32 là \(\dfrac{6}{20}=30\%\)
=>Sai
b: Sai
c: Sai
d: Sai

Giải:
(\(x-3\))\(^5\) = 4.(\(x-3\))\(^3\)
(\(x-3\))\(^5\) - 4.(\(x-3\))\(^3\) = 0
(\(x-3\))\(^3\).[(\(x-3)^2\) - 4] = 0
\(\left[\begin{array}{l}x-3=0\\ \left(x-3\right)^2=4\end{array}\right.\)
\(\left[\begin{array}{l}x=3\\ x-3=-2\\ x-3=2\end{array}\right.\)
\(\left[\begin{array}{l}x=3\\ x=-2+3\\ x=2+3\end{array}\right.\)
\(\left[\begin{array}{l}x=3\\ x=1\\ x=5\end{array}\right.\)
Vậy \(x\in\left\lbrace1;3;5\right\rbrace\)
(x - 3)⁵ = 4(x - 3)³
(x - 3)⁵ - 4(x - 3)³ = 0
(x - 3)³.[(x - 3)² - 4] = 0
(x - 3)³.(x - 3 - 2)(x - 3 + 2) = 0
(x - 3)³(x - 5)(x - 1) = 0
(x - 3)³ = 0 hoặc x - 5 = 0 hoặc x - 1 = 0
*) (x - 3)³ = 0
x - 3 = 0
x = 3
*) x - 5 = 0
x = 5
*) x - 1 = 0
x = 1
Vậy x = 1; x = 3; x = 5

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: ΔAHB=ΔAHC
=>\(\widehat{HAB}=\widehat{HAC}\)
=>AH là phân giác của góc BAC
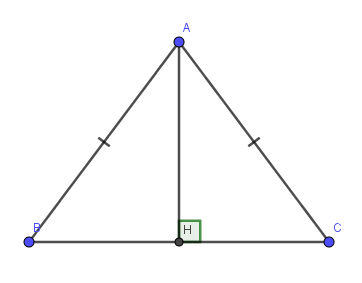
a) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:
\(AB=AC\left(gt\right)\)
\(AH\) là cạnh chung
\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)
b) Do \(\Delta AHB=\Delta AHC\left(cmt\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (hai góc tương ứng)
\(\Rightarrow AH\) là tia phân giác của \(\widehat{BAC}\)

a.
\(H\left(x\right)=A\left(x\right)+B\left(x\right)\)
\(H\left(x\right)=x^4+3x^3-5x^2+7x+\left(-x^4\right)-3x^3+5x^2+7\)
\(H\left(x\right)=7x+7\)
b.
\(K\left(x\right)=A\left(x\right)-B\left(x\right)\)
\(K\left(x\right)=x^4+3x^3-5x^2+7x-\left(-x^4-3x^3+5x^2+7\right)\)
\(K\left(x\right)=2x^4+6x^3-10x^2+7x-7\)
c.
\(H\left(x\right)=7x+7=0\)
\(7x=-7\)
\(x=-1\)
Vậy nghiệm của H(x) là \(x=-1\)

[3 x 3 - 7 x (+2)]: (2 x 2 - 3)
= [9 - 14):(4 - 3)
= - 5: 1
= - 5
H(\(x\)) = 3 - \(x^2\)
H(\(x\)) = 0 khi và chỉ khi:
3 - \(x^2\) = 0
\(x^2=3\)
\(\left[\begin{array}{l}x=-\sqrt3\\ x=\sqrt3\end{array}\right.\)
Vậy H(\(x\)) có hai nghiệm là: -\(\sqrt3\); \(\sqrt3\)