Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





a ta có
\(\left|x+\frac{1}{5}\right|-x+\frac{4}{7}\ge x+\frac{1}{5}-x+\frac{4}{7}=\frac{27}{35}\) dấu bằng xảy ra khi \(x\ge-\frac{1}{5}\)
b. \(\left|x-\frac{2006}{2007}\right|+\left|x-1\right|\ge\left|x-\frac{2006}{2007}-x+1\right|=\frac{1}{2007}\)
Dấu = xart ra khi \(\frac{2006}{2007}\le x\le1\)


Với x ≠ 0 và y ≠ 0 và 3x = 8y thì ta lập được các tỉ lệ thức sau :
\(\frac{x}{8}=\frac{y}{3};\frac{3}{8}=\frac{y}{x};\frac{3}{y}=\frac{8}{x};\frac{x}{y}=\frac{8}{3}\)
~~Học tốt~~

Gọi số cây trồng được của lớp 7A, 7B lần lượt là x (cây); y (cây).
Tỉ số giữa số cây trồng được của lớp 7A và lớp 7B là 0,8 nghĩa là x : y =0,8 hay
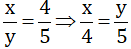
Lớp 7B trồng nhiều hơn lớp 7A là 20 cây nghĩa là y – x = 20.
Theo tính chất dãy tỉ số bằng nhau
Vậy Lớp 7A trồng được 80 cây
Lớp 7B trồng được 100 cây
7A: ██ cây
7B: ██ cây
[Lưu ý: Nếu không nhìn thấy đáp số thì là do mạng nha]




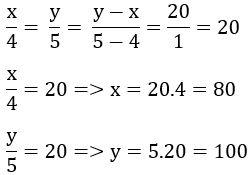
 Câu hỏi vì sao Bx//Cy nha câu hỏi trong hình bị sai đó
Câu hỏi vì sao Bx//Cy nha câu hỏi trong hình bị sai đó