Cho tam giác ABC. Lấy điểm M trên cạnh BC sao cho BM = 1/3 BC. Lấy điểm N trên cạnh AC sao cho AN = 2/3 AC. Biết diện tích tam giác AMN là 20cm2 . Tính diện tích tam giác ABC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi d = ƯCLN(2n + 3; 4n + 7)
⇒ (2n + 3) ⋮ d và (4n + 7) ⋮ d
*) (2n + 3) ⋮ d
⇒ 2(2n + 3) ⋮ d
⇒ (4n + 6) ⋮ d
Mà (4n + 7) ⋮ d (cmt)
⇒ (4n + 7 - 4n - 6) ⋮ d
⇒ 1 ⋮ d
⇒ d = 1
Vậy phân số đã cho là tối giản với mọi n là số nguyên

Bài 1:
a; (\(\dfrac{8}{19}\) + \(\dfrac{4}{21}\)) - 1\(\dfrac{3}{2020}\) - (\(\dfrac{27}{19}\) - \(\dfrac{17}{21}\))
= \(\dfrac{8}{19}\) + \(\dfrac{4}{21}\) - 1\(\dfrac{3}{2020}\) - \(\dfrac{27}{19}\) + \(\dfrac{17}{21}\)
= (\(\dfrac{8}{19}\) - \(\dfrac{27}{19}\)) + (\(\dfrac{4}{21}\) + \(\dfrac{17}{21}\)) - 1\(\dfrac{3}{2020}\)
= - \(\dfrac{19}{19}\) + \(\dfrac{21}{21}\) - 1\(\dfrac{3}{2020}\)
= -1 + 1 - 1\(\dfrac{3}{2020}\)
= 0 - 1\(\dfrac{3}{2020}\)
= -1\(\dfrac{3}{2020}\)
b; (\(\dfrac{-3}{4}\) + \(\dfrac{2}{5}\)): \(\dfrac{3}{7}\) + (\(\dfrac{3}{5}\) + \(\dfrac{-1}{4}\)): \(\dfrac{3}{7}\)
= (\(\dfrac{-3}{4}\) + \(\dfrac{2}{5}\)) x \(\dfrac{7}{3}\) + (\(\dfrac{3}{5}\) + \(\dfrac{-1}{4}\)) x \(\dfrac{7}{3}\)
= \(\dfrac{7}{3}\) x [ (\(-\dfrac{3}{4}\) + \(\dfrac{2}{5}\)) + (\(\dfrac{3}{5}\) + \(\dfrac{-1}{4}\))]
= \(\dfrac{7}{3}\) x [ - \(\dfrac{3}{4}\) + \(\dfrac{2}{5}\) + \(\dfrac{3}{5}\) - \(\dfrac{1}{4}\)]
= \(\dfrac{7}{3}\) x [- (\(\dfrac{3}{4}\) + \(\dfrac{1}{4}\)) + (\(\dfrac{2}{5}\) + \(\dfrac{3}{5}\))]
= \(\dfrac{7}{3}\) x [ - 1 + 1]
= \(\dfrac{7}{3}\) x 0
= 0

Gọi d=ƯCLN(2n+3;4n+7)
=>\(\left\{{}\begin{matrix}2n+3⋮d\\4n+7⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4n+6⋮d\\4n+7⋮d\end{matrix}\right.\)
=>\(4n+6-4n-7⋮d\)
=>\(-1⋮d\)
=>d=1
=>ƯCLN(2n+3;4n+7)=1
=>\(\dfrac{2n+3}{4n+7}\) là phân số tối giản

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: Ta có: \(\widehat{HAD}+\widehat{BDA}=90^0\)(ΔHAD vuông tại H)
\(\widehat{CAD}+\widehat{BAD}=\widehat{BAC}=90^0\)
mà \(\widehat{BDA}=\widehat{BAD}\)(ΔBAD cân tại B)
nên \(\widehat{HAD}=\widehat{CAD}\)
=>AD là phân giác của góc HAC
Xét ΔAHC có AD là phân giác
nên \(\dfrac{DH}{DC}=\dfrac{AH}{AC}\)
=>\(DH\cdot AC=AH\cdot DC\)

a:
Sửa đề: \(N\left(x\right)=3x^3-7x^2-x+\dfrac{3}{2}\)
M(x)+N(x)
\(=3x^3-7x^2+\dfrac{4}{5}x-\dfrac{1}{5}+3x^3-7x^2-x+\dfrac{3}{2}\)
\(=6x^3-14x^2-\dfrac{1}{5}x+\dfrac{13}{10}\)
b: H(x)=M(x)-N(x)
\(=3x^3-7x^2+\dfrac{4}{5}x-\dfrac{1}{5}-3x^3+7x^2+x-\dfrac{3}{2}\)
\(=\dfrac{9}{5}x-\dfrac{17}{10}\)
c: Đặt H(x)=0
=>\(\dfrac{9}{5}x-\dfrac{17}{10}=0\)
=>\(\dfrac{9}{5}x=\dfrac{17}{10}\)
=>\(x=\dfrac{17}{10}:\dfrac{9}{5}=\dfrac{17}{10}\cdot\dfrac{5}{9}=\dfrac{17}{18}\)
d: \(P\left(-1\right)=\left(-1\right)^3-3\cdot\left(-1\right)^2+3\cdot\left(-1\right)-1+2\cdot\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+5\)
\(=-1-3-3-1-2+1+1+5\)
=-3<0
=>x=-1 không là nghiệm của P(x)
\(P\left(x\right)=x^3-3x^2+3x-1+2x^3+x^2-x+5\)
\(=\left(x^3+2x^3\right)+\left(-3x^2+x^2\right)+\left(3x-x\right)+\left(-1+5\right)\)
\(=3x^3-2x^2+2x+4\)

ĐKXĐ: x<>-2
\(x^2+\dfrac{4x^2}{\left(x+2\right)^2}=5\)
=>\(\dfrac{\left(x^2+2x\right)^2+4x^2}{\left(x+2\right)^2}=5\)
=>\(x^4+4x^3+4x^2+4x^2=5\left(x^2+4x+4\right)\)
=>\(x^4+4x^3+8x^2-5x^2-20x-20=0\)
=>\(x^4+4x^3+3x^2-20x-20=0\)
=>\(\left(x-2\right)\left(x+1\right)\left(x^2+5x+10\right)=0\)
mà \(x^2+5x+10>0\forall x\)
nên (x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\left(nhận\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)

\(\dfrac{3}{5}\) giờ = \(36\) phút
Tỉ số phần trăm của a và b:
\(36.100\%:20=180\%\)


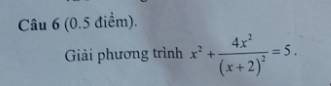
\(AN=\dfrac{2}{3}AC\)
=>AC=1,5AN
=>\(S_{AMC}=1,5\times S_{AMN}=1,5\times20=30\left(cm^2\right)\)
BM=1/3BC
=>\(CM=\dfrac{2}{3}CB\)
=>CB=1,5CM
=>\(S_{ABC}=1,5\times S_{AMC}=1,5\times30=45\left(cm^2\right)\)
Mik ko bt *^*