Cho ba số \(x,y,z\) thỏa mãn điều kiện \(z\ge y\ge x\ge0\). Chứng minh rẳng
\(x\left(x-y\right)\left(x-z\right)+y\left(y-z\right)\left(y-x\right)+z\left(z-x\right)\left(z-y\right)\ge0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
12 tháng 3 2022
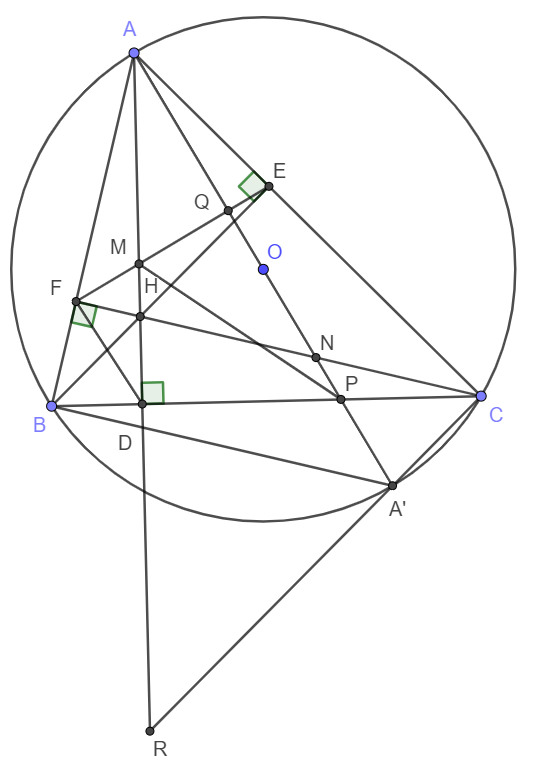
a) theo gt, BFC=BEC=90
=> BFEC nội tiếp (có 2 góc kề bang nhau)
góc AFC=ADC=90 => AFDC nội tiếp ( có 2 cạnh kề cùng nhìn một đoan thẳng bằng nhau)
b) vì tứ giác ABA'C nội tiếp => ABC = AA'C (cùng chắn cung AC)
Lại có ABC= AHF (Cùng phụ với góc BAD)
Ta thấy AFHE nội tiếp vì AFH +AEH = 90+90=180
=> AHF=AEF (Cùng chắn cung AF)
=>Đpcm
c) vì tứ giác EQA'C nôi tiếp
nên EQA'+ECA'=180 mà ECA'=90 vì là góc nội tiếp chắn nửa đường tròn
=> MQP=EQA'=90 ( vì MQP+EQA=180)
Trong đó ADC=90 =>Đpcm
d) Vì ABA'C VÀ FBDH nội tiếp nên góc NA'C=ABC=DHC
=>NA'C=DHC=>Đpcm
12 tháng 3 2022
c
Cho tam giác ABCABC vuông tại AA. Nửa đường tròn đường kính ABAB cắt BCBC tại DD. Trên cung ADAD lấy một điểm EE. Nối BEBE và kéo dài cắt ACAC tại FF. Chứng minh CDEFCDEF là tứ giác nội tiếp.
theo gt, ta có: DAB = BCA= 90 - CBA
(Tính chất tổng các góc trong tam giác BCA và tam giác BAD)
Mặt khác DEB = DAB ( Cùng chắn cung DB)
=> DEB= BCA => Đpcm
12 tháng 3 2022
Cho tam giác ABCABC cân tại AA và nội tiếp đường tròn tâm OO, đường kính AIAI. Gọi EE là trung điểm của ABAB, KK là trung điểm của OIOI, HH là trung điểm của EBEB.
a/ Chứng minh HK\perp EBHK⊥EB
b/ Chứng minh tứ giác AEKCAEKC nội tiếp được trong một đường tròn.
a) Ta thấy E, O là trung điểm của AB và AI nên EO là đường trung bình tam giác ABI
\Rightarrow⇒ EO song song với BI.
Ta lại có H, K lần lượt là trung điểm của EB và OI
nên HK là đường trung bình của hình thang EOIB.
=> HK song song với BI (1)
Mặt khác do AI là đường kính nên góc ABI = 90 (2)\widehat{ABI}=90^o
Từ (1) và (2) suy ra HK\perp EBHK vuông góc với EB(đpcm)
b)
Xét tam giác KBE có KH là trung tuyến đồng thời đường cao (CM trước)
nên KBE là tam giác cân tại K.
=> góc BEK = KBE (3)
Do tam giác ABC cân tại A
nên AI là đường trung trực của BC
Mà K thuộc AI nên KB = KC
hay tam giác KBC cân tại K
=> KBC=KCB
và ACB=ABC
.Mặt khác, ta lại có ACB= ACK + KCB và ABC = ABK + KBC
=> ABK=ACK(4)
Từ (3) và (4) suy ra \widehat{BEK}=\widehat{KCA}
.
AEKC là tứ giác nội tiếp.