a, vì bộ bài có 52 lá,lá át cơ chỉ có một

=>xác xuất của biến cố bác tuân rút ra lá at cơ là 1/52 hoặc 5,2%

(có thiếu hay sai chỗ nào trong bài của mik ko các bạn?)

a: Xét ΔAHB và ΔAHC có

AH chung

\(\widehat{BAH}=\widehat{CAH}\)

AB=AC

Do đó: ΔAHB=ΔAHC

=>\(\widehat{AHB}=\widehat{AHC}\)

mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)

nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)

=>AH\(\perp\)BC

b: ΔAHB=ΔAHC

=>HB=HC

=>H là trung điểm của BC

Xét ΔABC có

BD,AH là các đường trung tuyến

BD cắt AH tại G

Do đó: G là trọng tâm của ΔABC

Xét ΔABC có

H là trung điểm của BC

HK//AC

Do đó: K là trung điểm của AB

Xét ΔABC có

G là trọng tâm

K là trung điểm của AB

Do đó: C,G,K thẳng hàng

a,Xét tam giác ABD và tam giác EBD có

góc DAB = góc DEB = 90°

DB chung

góc ABD = góc EBD ( DB là tia phân giác )

=> tam giác ABD = EBD (g.c.g)

b,xét tam giác AND và tam giác ECD có

góc NAD = góc CED = 90°

AD = DE ( tam giác ABD = tam giác EBD )

góc ADN = góc EDC ( 2 góc đối đỉnh )

=> tam giác NAD = CED (g.c.g)

=> AN = EC

c, ta có CA vuông góc NB ( tam giác ABC vuông tại A )

NE vuông góc CB ( DE vuông góc CB )

=> điểm D là trực tâm của tam giác NBC

=> DB vuông góc NC

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

b: ΔABC cân tại A

mà AM là đường trung tuyến

nên AM là đường trung trực của BC

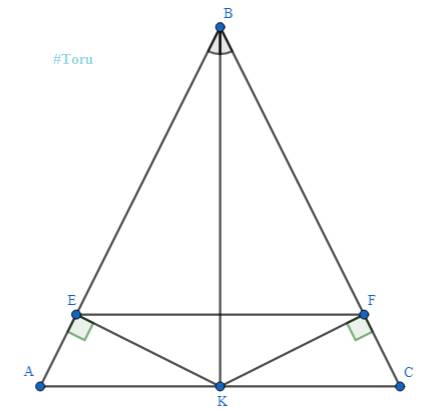
a) Xét \(\Delta BAK\) và \(\Delta BCK\) có: 

\(\left\{{}\begin{matrix}AB=AC\left(\Delta ABC\text{ cân tại }A\right)\\\widehat{ABK}=\widehat{CBK}\left(BK\text{ là tia phân giác }\widehat{ABC}\right)\\BK\text{ chung}\end{matrix}\right.\)

\(\Rightarrow\Delta BAK=\Delta BCK\left(c.g.c\right)\)

b) Vì \(\Delta ABC\) cân tại B \(\Rightarrow\widehat{BAC}=\widehat{BCA}\) (t/c)

hay \(\widehat{EAK}=\widehat{FCK}\) (vì \(E\in AB;F\in AC;K\in BC\))

Vì \(\Delta BAK=\Delta BCK (cmt)\Rightarrow AK=CK\) (hai cạnh tương ứng)

Xét \(\Delta AKE\) và \(\Delta CKF\) có:

\(\left\{{}\begin{matrix}\widehat{AEK}=\widehat{CFK}=90^{\circ}\left(KE\bot AB;KF\bot AC\right)\\AK=CK\left(cmt\right)\\\widehat{EAK}=\widehat{FCK}\left(cmt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta AKE=\Delta CKF\left(ch.gn\right)\) \(\Rightarrow KE=KF\) (hai cạnh tương ứng)

\(\Rightarrow\Delta KEF\) cân tại K

$\text{#}Toru$

Mn ng giúp mình vs nha 

Mình cần gấp 

Có hình nữa nhé

a: Xét ΔAHB và ΔAHC có

AH chung

HB=HC

AB=AC

Do đó: ΔAHB=ΔAHC

=>\(\widehat{AHB}=\widehat{AHC}\)

mà \(\widehat{AHB}+\widehat{AHC}=180^0\)(hai góc kề bù)

nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)

=>AH\(\perp\)BC

b: Xét ΔIBC có

IH là đường cao

IH là đường trung tuyến

Do đó: ΔIBC cân tại I

c: ta có: MN//BC

AH\(\perp\)BC

Do đó;AH\(\perp\)MN tại A

ta có: MN//BC

=>\(\widehat{IMN}=\widehat{IBC};\widehat{INM}=\widehat{ICB}\)

mà \(\widehat{IBC}=\widehat{ICB}\)(ΔIBC cân tại I)

nên \(\widehat{IMN}=\widehat{INM}\)

=>ΔINM cân tại I

ta có: ΔINM cân tại I

mà IA là đường cao

nên A là trung điểm của MN

d: Xét ΔAEI vuông tại E và ΔAFI vuông tại F có

AI chung

\(\widehat{EAI}=\widehat{FAI}\)

Do đó: ΔAEI=ΔAFI

=>IE=IF

Xét ΔBEI vuông tại E và ΔBHI vuông tại H có

BI chung

\(\widehat{EBI}=\widehat{HBI}\)

Do đó: ΔBEI=ΔBHI

=>IE=IH

=>IE=IF=IH

\(B=6x^4+5x^2y^2+y^4+6x^2-2\)

\(=6x^4+2x^2y^2+3x^2y^2+y^4+6x^2-2\)

\(=2x^2\left(3x^2+y^2\right)+y^2\left(3x^2+y^2\right)+6x^2-2\)

\(=12x^2+18y^2+6x^2-2\)

\(=18x^2+18y^2-2=18x^2+6y^2+12y^2-2\)

\(=6\left(3x^2+y^2\right)+12y^2-2=36+12y^2-2=12y^2+34\)