Cho tam giác ABC có góc A nhọn, BD và CE là 2 đường cao. H là trực tâm
a) C/m rằng ADHE và BDCE là tứ giác nội tiếp
b) C/m AE.AB = AD.AC = AO^2 - R^2. Biết O, R lần lượt là tâm và bán kính của đường tròn ngoại tiếp tứ giác BCDE
#Toán lớp 9Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

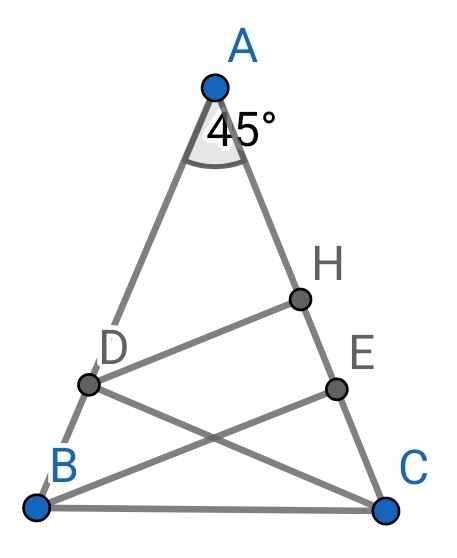
a) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2
= (180⁰ - 45⁰) : 2
= 67,5⁰
Do ∠ABC = ∠ACB > ∠BAC (67,5⁰ = 67,5⁰ > 45⁰)
⇒ AC = AB > BC
b) Do ∠ABC = ∠ACB (cmt)
⇒ ∠DBC = ∠ECB
Xét ∆BCD và ∆CBE có:
BD = CE (gt)
∠DBC = ∠ECB (cmt)
BC là cạnh chung
⇒ ∆BCD = ∆CBE (c-g-c)
⇒ ∠BDC = ∠CEB (hai góc tương ứng)

a) Số học sinh loại giỏi:
120 . 1/6 = 20 (học sinh)
Số học sinh khá:
120 . 30% = 36 (học sinh)
Số học sinh trung bình:
120 . 1/3 = 40 (học sinh)
Số học sinh yếu:
120 - 20 - 36 - 40 = 24 (học sinh)
b) Tỉ số phần trăm của số học sinh yếu so với cả lớp:
24 . 100% : 120 = 20%

Có 7 cách chọn chữ số hàng đơn vị
Có 6 cách chọn chữ số hàng chục
Có 5 cách chọn chữ số hàng trăm
Số số tự nhiên có thể lập được là:
5.6.7 = 210 (số)

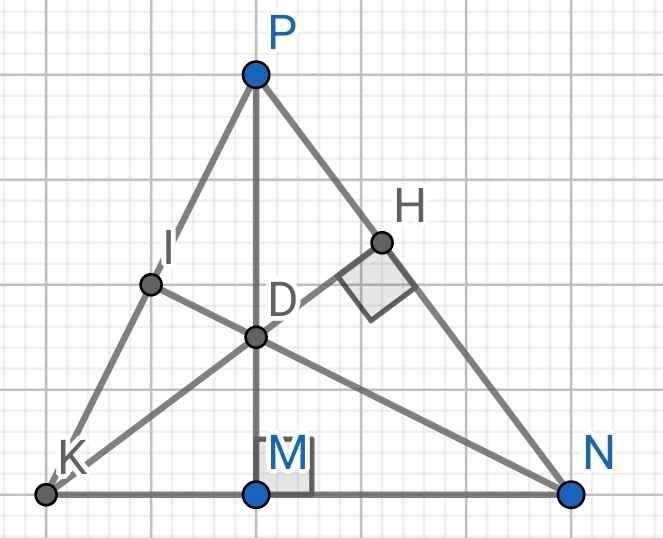
a) Do ND là đường phân giác của ∆MNP (gt)
⇒ ∠MND = ∠PND
⇒ ∠MND = ∠HND
Xét hai tam giác vuông: ∆MND và ∆HND có:
ND là cạnh chung
∠MND = ∠HND (cmt)
⇒ ∆MND = ∆HND (cạnh huyền - góc nhọn)
b) Do ∆MND = ∆HND (cmt)
⇒ MN = HN (hai cạnh tương ứng)
c) Do ∆MND = ∆HND (cmt)
⇒ MD = HD (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆DMK và ∆DHP có:
MD = HD (cmt)
∠MDK = ∠HDP (đối đỉnh)
⇒ ∆DMK = ∆DHP (cạnh góc vuông - góc nhọn kề)
⇒ MK = HP (hai cạnh tương ứng)
Lại có: MN = HN (cmt)
⇒ MK + MN = HP + HN
⇒ KN = PN
⇒ ∆NPK cân tại N
Do ∆MNP vuông tại M (gt)
⇒ PM ⊥ MN
⇒ PM ⊥ NK
⇒ PM là đường cao của ∆NPK
Lại có:
DH ⊥ NP (gt)
⇒ KH ⊥ NP
⇒ KH là đường cao thứ hai của ∆NPK
⇒ ND là đường cao thứ ba của ∆NPK
Mà ∆NPK cân tại N (cmt)
⇒ ND cũng là đường trung tuyến của ∆NPK
⇒ ND đi qua trung điểm của PK
Mà I là trung điểm của PK
⇒ N, D, I thẳng hàng

a: A(x)+B(x)
\(=8x^4+8x^3-6x-15+8x^4+8x^3-4x^2-6x-10\)
\(=16x^4+16x^3-4x^2-12x-25\)
b: B(x)-A(x)
\(=8x^4+8x^3-4x^2-6x-10-8x^4-8x^3+6x+15\)
\(=-4x^2+5\)
c: \(C\left(x\right)\cdot\left(B\left(x\right)-A\left(x\right)\right)=\left(x+1\right)\left(-4x^2+5\right)\)
\(=-4x^3+5x-4x^2+5\)

Công thức tính diện tích đáy của hình lăng trụ đứng còn tùy thuộc xem đáy của hình lăng trụ đứng đó là hình gì em nhé.
+ Nếu đáy là hình tam giác sử dụng công thức tính diện tích hình tam giác
+ Nếu đáy là hình chữ nhật sử dụng công thức tính diện tích hình chữ nhật
+ Nếu đáy là hình thang sử dụng công thức tính diện tích hình thang.
+ Nếu đáy là hình tròn sử dụng công thức tính diện tích hình tròn.
+ Nếu đáy là hình vuông sử dụng công thức tính diện tích hình vuông.
+ Nếu đáy là hình thoi sử dụng công thức tính diện tích hình thoi.
+ Nếu đáy là bình hành thì sử dụng công thức tính diện tích hình bình hành.
+ Nếu đáy là hình khác biệt thì chia đáy đó thành hình thông thường, tính diện tích từng hình, cộng tất cả diện tích các hình thông thường đó ta được diện tích đáy.
Công thức tính diện tích đáy của hình lăng trụ đứng còn tùy thuộc xem đáy của hình lăng trụ đứng đó là hình gì em nhé.
+ Nếu đáy là hình tam giác sử dụng công thức tính diện tích hình tam giác
+ Nếu đáy là hình chữ nhật sử dụng công thức tính diện tích hình chữ nhật
+ Nếu đáy là hình thang sử dụng công thức tính diện tích hình thang.
+ Nếu đáy là hình tròn sử dụng công thức tính diện tích hình tròn.
+ Nếu đáy là hình vuông sử dụng công thức tính diện tích hình vuông.
+ Nếu đáy là hình thoi sử dụng công thức tính diện tích hình thoi.
+ Nếu đáy là bình hành thì sử dụng công thức tính diện tích hình bình hành.
+ Nếu đáy là hình khác biệt thì chia đáy đó thành hình thông thường, tính diện tích từng hình, cộng tất cả diện tích các hình thông thường đó ta được diện tích đáy.

Pt hoành độ giao điểm:
\(\dfrac{1}{2}x^2=2x-m+1\Leftrightarrow x^2-4x+2m-2=0\) (1)
(d) cắt (P) tại 2 điểm pb nằm về 2 phía trục tung khi và chỉ khi (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow x_1x_2=2m-2< 0\)
\(\Leftrightarrow m< 1\)

Px = 3x mũ 5 + 4x mũ 4 - 2x mũ 3 - 5
-
Qx = - 3x mũ 5 - 4x mũ 4 + 2x mũ 3 - 3x mũ 2 + 1
----------------------------------------------------------------------------
Px + Qx = 6x mũ 5 + 8x mũ 4 - 4x mũ 3 -2x mũ + 3x mũ 2 + 4
b, ???
a: Xét tứ giác ADHE có \(\widehat{ADH}+\widehat{AEH}=90^0+90^0=180^0\)
nên ADHE là tứ giác nội tiếp
Xét tứ giác BEDC có \(\widehat{BEC}=\widehat{BDC}=90^0\)
nên BEDC là tứ giác nội tiếp
b: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB~ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(AD\cdot AC=AB\cdot AE\)