Gọi A là biến cố "Số xuất hiện trên thẻ được rút ra là số chia 4 dư 2"

=>A={2;6;10;14;18;22;26;30}

=>n(A)=8

\(n\left(\Omega\right)=30-1+1=30\)

\(P_A=\dfrac{8}{30}=\dfrac{4}{15}\)

Góc ACB bằng cái gì thế em?

Chọn D

Đề sai

Bài 1

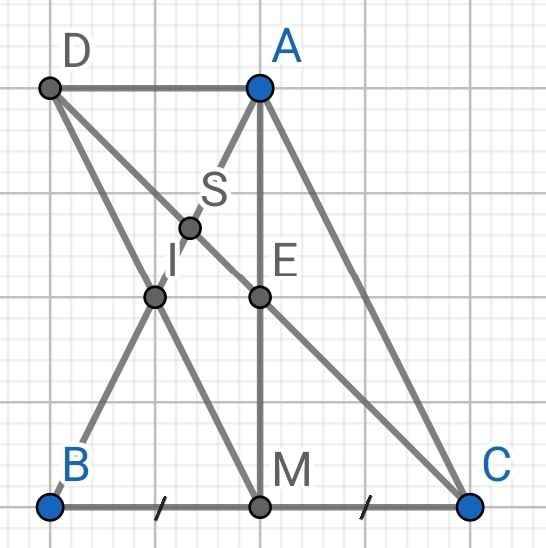
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Do M là trung điểm của BC (gt)

⇒ BM = MC

Xét ∆AMB và ∆AMC có:

AB = AC (cmt)

BC = MC (cmt)

AM là cạnh chung

⇒ ∆AMB = ∆AMC (c-c-c)

b) Do AD // BC (gt)

⇒ AD // BM

⇒ ∠DAI = ∠MBI (so le trong)

Xét ∆AID và ∆BIM có:

∠DAI = ∠MBI (cmt)

AI = BI (do I là trung điểm của AB)

∠AID = ∠BIM (đối đỉnh)

⇒ ∆AID = ∆BIM (g-c-g)

⇒ AD = BM (hai cạnh tương ứng)

Mà BM = MC (cmt)

⇒ AD = MC

c) ∆AMB = ∆AMC (cmt)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180⁰ (kề bù)

⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰

⇒ AM ⊥ BC

⇒ ∠AMC = ∠EMC = 90⁰

⇒ ∆MCE vuông tại M

Mà AD // BC (cmt)

⇒ AD ⊥ AM

⇒ ∠DAM = ∠DAE = 90⁰

⇒ ∆ADE vuông tại A

Do AD // BC (gt)

⇒ ∠ADE = ∠MCE (so le trong)

Xét hai tam giác vuông: ∆ADE và ∆MCE có:

AD = MC (cmt)

∠ADE = ∠MCE (cmt)

⇒ ∆ADE = ∆MCE (cạnh góc vuông - góc nhọn kề)

⇒ AE = ME (hai cạnh tương ứng)

⇒ E là trung điểm của AM

Do ∆AID = ∆BIM (cmt)

⇒ ID = IM (hai cạnh tương ứng)

⇒ I là trung điểm của MD

∆ADM có:

AI là đường trung tuyến (do I là trung điểm của MD)

DE là đường trung tuyến (do E là trung điểm của AM)

Mà AI và DE cắt nhau tại S

⇒ S là trọng tâm của ∆ADE

⇒ AS = 2SI

⇒ 3AS = 6SI

Lại có:

AI = BI (cmt)

⇒ AB = AI + BI = 3SI + 3SI = 6SI

⇒ AB = 3AS

Mà AB > BC (gt)

⇒ 3AS > BC

Hay BC < 3AS

Bài 3

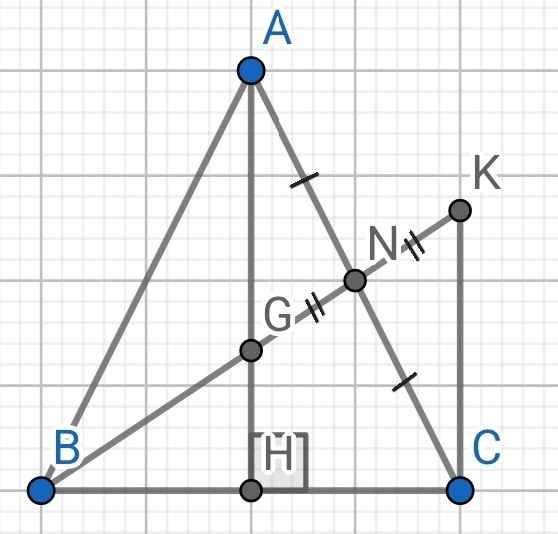
a) Do ∆ABC cân tại A (gt)

⇒ AB = AC

Xét hai tam giác vuông: ∆ABH và ∆ACH có:

AB = AC (cmt)

AH là cạnh chung

⇒ ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)

b) ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH cũng là đường trung tuyến của ∆ABC

Lại có N là trung điểm của AC (gt)

⇒ BN là đường trung tuyến thứ hai của ∆ABC

Mà AH và BN cắt nhau tại G (gt)

⇒ G là trọng tâm của ∆ABC

Xét ∆ANG và ∆CNK có:

AN = CN (do N là trung điểm của AC)

∠ANG = ∠CNK (đối đỉnh)

NG = NK (gt)

⇒ ∆ANG = ∆CNK (c-g-c)

⇒ ∠AGN = ∠CKN (hai góc tương ứng)

Mà ∠AGN và ∠CKN là hai góc so le trong

⇒ AG // CK

c) Do G là trọng tâm của ∆ABC (cmt)

⇒ AG = 2GN

Lại có:

NG = NK (gt)

⇒ GK = 2GN

Mà BG = 2GN (cmt)

⇒ BG = GK

⇒ G là trung điểm của BK

a: Xét ΔABM và ΔACM có

AB=AC

BM=CM

AM chung

Do đó: ΔABM=ΔACM

b: Xét ΔMHB vuông tại H và ΔMKC vuông tại K có

MB=MC

\(\widehat{B}=\widehat{C}\)

Do đó: ΔMHB=ΔMKC

Ta có: BH\(\perp\)AC(H là trực tâm của ΔABC)

CD\(\perp\)AC

Do đó: BH//CD
Ta có: CH\(\perp\)AB(H là trực tâm của ΔABC)

BD\(\perp\)AB

Do đó: CH//BD

Giả sử tồn tại các số thực a;b;c đôi một phân biệt thỏa mãn

Áp dụng t/c dãy tỉ số bằng nhau:

\(\dfrac{a}{a^2+9}=\dfrac{b}{b^2+9}=\dfrac{c}{c^2+9}=\dfrac{a-b}{a^2-b^2}=\dfrac{a-c}{a^2-c^2}=\dfrac{1}{a+b}=\dfrac{1}{a+c}\)

\(\Rightarrow a+b=a+c\Rightarrow b=c\) (mâu thuẫn giả thiết b,c phân biệt)

Vậy điều giả sử là sai, hay ko tồn tại 3 số thực a;b;c phân biệt thỏa mãn yêu cầu

a: Xét ΔAIB và ΔAIC có

AB=AC

IB=IC

AI chung

Do đó: ΔAIB=ΔAIC

b: ΔAIB=ΔAIC

=>\(\widehat{AIB}=\widehat{AIC}\)

mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)

nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)

Xét ΔDIB vuông tại I và ΔDIC vuông tại I có

DI chung

IB=IC

Do đó: ΔDIB=ΔDIC

=>DB=DC

c: Vì DB=DE

mà D nằm giữa B và E

nên D là trung điểm của BE

Xét ΔEBC có

EI,CD là các đường trung tuyến

EI cắt CD tại G

Do đó: G là trọng tâm của ΔEBC

=>EG=2GI

Rồi em cần làm gì với hai đa thức đó?