C = 202.25 + 303.9 – 101.67
mn giúp mình vs pls
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{4}{1.5}\) + \(\dfrac{4}{5.9}\) + \(\dfrac{4}{9.13}\) + \(\dfrac{4}{13.17}\) + ... + \(\dfrac{4}{99.103}\)
= \(\dfrac{1}{1}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{9}\) + \(\dfrac{1}{9}\) - \(\dfrac{1}{13}\) + \(\dfrac{1}{13}\) - \(\dfrac{1}{17}\) + \(\dfrac{1}{99}\) - \(\dfrac{1}{103}\)
= \(\dfrac{1}{1}\) - \(\dfrac{1}{103}\)
= \(\dfrac{102}{103}\)

Giải:
Theo bài ra ta có: \(\left\{{}\begin{matrix}a=12.k\\b=12.d\end{matrix}\right.\) (k; d) = 1; k;d \(\in\) N*
12k.12.d = 180.12
k.d = 180.12 : (12.12) = 15
Ư(15) = {1; 3; 5; 15}
Lập bảng ta có:
| k.d | 15 | 15 | 15 | 15 |
| k | 1 | 3 | 5 | 15 |
| d | 15 | 5 | 3 | 1 |
| (k;d)=1 | nhận | nhận | nhận | nhận |
Theo bảng trên ta có: (k;d) =(1; 15); (3; 5); (5; 3); (15; 1)
Vậy: (a;b) = (12; 180); (36; 60); (60; 36); (180; 12)

Vì \(AI=\dfrac{1}{3}AC\)
nên \(S_{ABI}=\dfrac{1}{3}\cdot S_{ABC}=\dfrac{1}{3}\cdot120=40\left(cm^2\right)\)
Vì D là trung điểm của AB nên AD=1/2BA
=>\(S_{ADI}=\dfrac{1}{2}\cdot S_{ABI}=\dfrac{1}{2}\cdot40=20\left(cm^2\right)\)

Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian đi từ A đến B là \(\dfrac{x}{40}\left(giờ\right)\)
Thời gian đi từ B về A là \(\dfrac{x}{32}\left(giờ\right)\)
Thời gian đi ít hơn thời gian về là 1 giờ nên \(\dfrac{x}{32}-\dfrac{x}{40}=1\)
=>\(\dfrac{5x-4x}{160}=1\)
=>\(\dfrac{x}{160}=1\)
=>x=160(nhận)
vậy: Độ dài quãng đường AB là 160km
Giải:
Cùng một quãng đường vận tốc tỉ lệ nghịch với thời gian.
Tỉ số thời gian lúc đi và thời gian lúc về là: 32 : 40 = \(\dfrac{4}{5}\)
Gọi thời gian lúc đi là t (giờ); t > 0
Thì thời gian lúc về là: 1 : \(\dfrac{4}{5}\) x t = \(\dfrac{5}{4}\)t
Theo bài ra ta có: \(\dfrac{5}{4}\)t - t = 1
t.(\(\dfrac{5}{4}-1\)) =1
\(\dfrac{1}{4}\)t = 1
t = 4 x 1
t = 4
Vậy Thời gian đi từ A đến B là 4 giờ.
Quãng đường từ A đến B dài là: 4 x 40 = 160 (km)
Kết luận: Quãng đường AB dài 160 km.

Câu a tự làm;
Câu b:
Hoành độ giao điểm là nghiệm của phương trình:
\(x^2\) = - 2\(x\) + 3
\(x^2\) + 2\(x\) - 3 = 0
a + b - c = 1 + 2 - 3 = 0
Phương trình có hai nghiệm phân biệt là:
\(x_1\) = 1; \(x_2\) = -3
\(x_1\) = 1 ⇒ y1 = (1)2 = 1
\(x_2\) = - 3 ⇒ y2 = (-3)2 = 9
Vậy (P) và (d) cắt nhau tai hai điểm có tọa độ lần lượt là:
A(1; 1); B(-3; 9)
a: 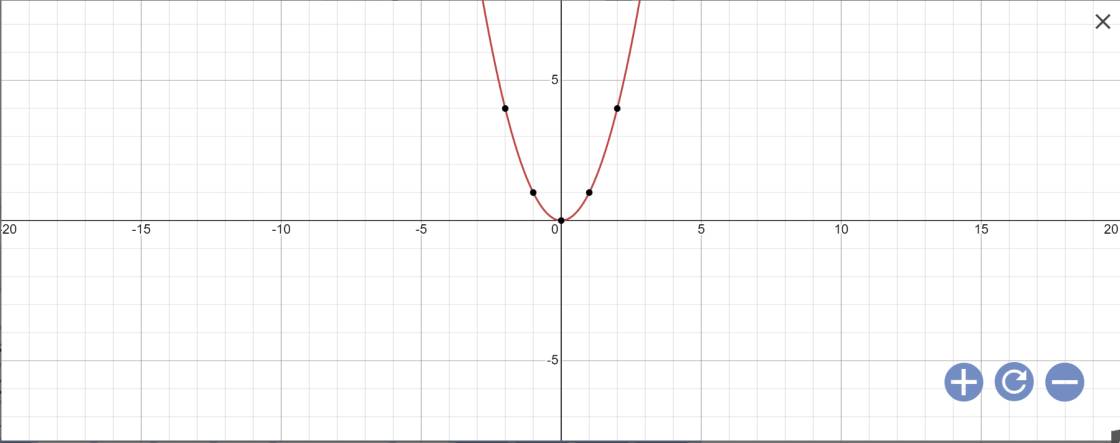
b: Phương trình hoành độ giao điểm là:
\(x^2=-2x+3\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Thay x=-3 vào y=-2x+3, ta được:
\(y=-2\cdot\left(-3\right)+3=9\)
Thay x=1 vào y=-2x+3, ta được:
\(y=-2\cdot1+3=1\)
Vậy: (d) cắt (P) tại A(-3;9); B(1;1)

vậy hiệu hai số là : 125 x 2 =250
Số bé là : 4083-250=3833
Tổng là:4083+3833=7916
vậy hiệu hai số là : 125 x 2 =250
Số bé là : 4083-250=3833
Tổng là:4083+3833=7916
Đáp số:....
Đây nha em

1+(-2)+3+(-4)+5+(-6)+....+47+(-48)+49+(-50)
(-1)+(-1)+(-1)+...+(-1)
Có số cặp có hiệu -1 là: 50:2=25( cặp)
=> (-1) x 25
=-25
Đây nha

Do xy=1 nên ta biến đối vế trái để bài toán trở thành Chứng minh BĐT sau:
\(\dfrac{4}{\left(x+y\right)^2}-2\dfrac{2}{\left(x+y\right)}\left(x+y\right)+\left(x^2+2xy+y^2\right)+2\ge3\)
Hay: \(\dfrac{4}{\left(x+y\right)^2}-2\dfrac{2}{\left(x+y\right)}\left(x+y\right)+\left(x+y\right)^2\ge1\)
<==> \(\left(\dfrac{2}{x+y}-\left(x+y\right)\right)^2\ge1\) quy đồng mẫu số vế trái:
<==> \(\left(\dfrac{-\left(x^2+y^2\right)}{x+y}\right)^2\ge1\) (do xy=1)
<==> \(\left(\dfrac{\left(x^2+y^2\right)}{x+y}\right)^2\ge1\) (*)
(vì vế trái là Bình phương 1 phân số nên ta có thể bỏ qua dấu âm của tử số).
Xét vế trái của (*):
Áp dụng BĐT Bunhiacopxki cho mẫu số: (x+y) ≤ \(\sqrt{2}\cdot\sqrt{x^2+y^2}\)
(Đẳng thức khi x=y)
Khi đó Vế trái BĐT (*) : \(\left(\dfrac{\left(x^2+y^2\right)}{x+y}\right)^2\ge\left(\dfrac{\left(x^2+y^2\right)}{\sqrt{2\left(x^2+y^2\right)}}\right)^2=\dfrac{\left(x^2+y^2\right)}{2}\) (**)
Áp dụng BĐT Cô sy cho tử số (cả x2 và y2 đều là số dương) ta có:
(x2+y2) ≥ 2xy =2 (do xy=1) Đẳng thức khi x=y. ==> (**) ≥1
Đó chính là Đpcm (*). (Đẳng thức khi x=y=1).
C = 202.25 + 303.9 - 101.67
C = 101.2.25 + 101.3.9 - 101.67
C = 101.(2.25 + 3.9 - 67)
C = 101.(50 + 27 - 67)
C = 101. 10
C = 1010
em cảm ơn cô ạ