số các số tự nhiên lẻ có 3 chữ số là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A = \(-\frac{3}{2.5}\) + \(\frac{-3}{5.8}\) + \(-\frac{3}{8.11}\) + ....+ \(-\frac{3}{97.100}\)
A = - (\(\frac{3}{2.5}\) + \(\frac{3}{5.8}\) + \(\frac{3}{8.11}\) + ... + \(\frac{3}{97.100}\))
A = - (\(\frac12-\frac15\) + \(\frac18\) - \(\frac{1}{11}\) + ...+ \(\frac{1}{97}-\frac{1}{100}\))
A = - \(\frac12\) + \(\frac{1}{100}\)
A = \(-\frac{49}{100}\)

Gọi x là số sách của thư viện.
Theo đề bài, ta có:
\(x⋮12\)
\(x⋮15\)
\(x⋮18\)
\(\Rightarrow x\in BC\left(12;15;18\right)\)
Ta có: \(12=2^2.3\)
\(15=3.5\)
\(18=2.3^2\)
\(BCNN\left(12;15;18\right)=2^2.3^2.5=4.9.5=180\)
\(BC\left(12;15;18\right)=B\left(180\right)=\left\{0;180;360;540;720;900;...\right\}\)
Vì số sách của thư viện có khoảng từ 600 đến 800 nên \(x=720\) ( quyển ).
Vậy...
\(#Nulc`\)

\(-\frac{4}{12}+\frac{18}{45}-\frac{6}{9}-\frac{21}{35}+\frac{6}{30}\)
\(=\frac{-1}{3}+\frac{2}{5}-\frac{1}{3}-\frac{3}{5}+\frac{1}{5}\)
\(=0\)

\(a.\dfrac{x}{7}=\dfrac{-4}{14}\)
\(x\times14=-4\times7\)
\(x=\dfrac{-4\times7}{14}\)
\(x=-2\)
Vậy \(x=-2\)
\(b,\dfrac{x+3}{2}=\dfrac{-12}{-6}\dfrac{ }{ }\)
\(\dfrac{x+3}{2}=2\)
\(x+3=2\times2\)
\(x+3=4\)
\(x=4-3\)
\(x=1\)
Vậy \(x=1\)
\(c,\dfrac{x}{2}=\dfrac{-2}{-x}\)
\(\dfrac{x}{2}=\dfrac{2}{x}\)
\(x^2-2\times2\)
\(x^2=4\)
\(x^2=2^2\) hoặc \(x^2=\left(-2\right)^2\)
\(x=2\) \(x=-2\)
Vậy \(x\in\left\{2;-2\right\}\)
\(d,\dfrac{x-1}{5}=\dfrac{5}{x-1}\)
\(\left(x-1\right)^2=5\times5\)
\(\left(x-1\right)^2=25\)
\(\left(x-1\right)^2=5^2\) hoặc \(\left(x-1\right)^2=\left(-5\right)^2\)
\(x-1=5\) \(x-1=-5\)
\(x=5+1\) \(x=-5+1\)
\(x=6\) \(x=-4\)
Vậy \(x\in\left\{6;-4\right\}\)
\(a;\dfrac{x}{7}=-\dfrac{4}{14}\\ =>x=\dfrac{\left(-4\right)\cdot7}{14}=-2\\ b;x+\dfrac{3}{2}=\dfrac{-12}{-6}\\ =>x=\dfrac{1}{2}+\dfrac{3}{2}=\dfrac{1}{2}\\ c;\dfrac{x}{2}=\dfrac{-2}{-x}< =>\dfrac{x}{2}=\dfrac{2}{x}\\ =>x^2=4=>x=\pm2\\ d;\dfrac{x-1}{5}=\dfrac{5}{x-1}\\ =>\left(x-1\right)^2=25\\ =>\left[{}\begin{matrix}x-1=5=>x=6\\x-1=-5=>x=-4\end{matrix}\right.\)


chieu cao hinh thang la :
`84 xx 2 :7 = 24(cm)`
đáy ban đầu hình thang là :
`120 xx 2 : 24 = 10(cm)`
Đáp số : `10cm`

Bước 1: Vẽ đoạn thẳng MN
- Vẽ một đoạn thẳng MN dài 10 cm.
Bước 2: Đánh dấu điểm A
- Lấy điểm A thuộc đoạn thẳng MN sao cho \(A N = 4\) cm. Điều này có nghĩa là điểm A cách điểm N 4 cm.
- Do đó, đoạn MA sẽ có độ dài là: \(M A = M N - A N = 10 \textrm{ } \text{cm} - 4 \textrm{ } \text{cm} = 6 \textrm{ } \text{cm}\)
Bước 3: Đánh dấu điểm B
- Lấy điểm B nằm giữa M và A. Do đó, điểm B sẽ nằm trên đoạn MA.
Bước 4: Đánh dấu điểm C
- Lấy điểm C trùng với điểm A. Như vậy, C = A.
Bước 5: Tính toán số đoạn thẳng
- Trong hình có các đoạn thẳng sau:
- Đoạn thẳng MN (1 đoạn)
- Đoạn thẳng MA (1 đoạn)
- Đoạn thẳng AB (1 đoạn)
- Đoạn thẳng AC (1 đoạn)
- Đoạn thẳng MB (1 đoạn)
Kết luận
- Tổng số đoạn thẳng trong hình là: \(5 \textrm{ } đ\text{o}ạ\text{n}\&\text{nbsp};\text{th}ẳ\text{ng}\)
Kết quả cuối cùng
- Độ dài đoạn thẳng MA là 6 cm.
- Số đoạn thẳng trong hình là 5 đoạn thẳng.
a: Ta có: A thuộc đoạn MN
=>A nằm giữa M và N
=>AM+AN=MN
=>AM=MN-AN=10-4=6(cm)
b: Các đoạn thẳng trong hình vẽ là: MB,MA,MN,BA,BN,AN,CA,CM,CB,CN
=>Có 10 đoạn thẳng

\(\left(x+\dfrac{1}{2}\right)\left(x-\dfrac{x}{3}\right)=0\)
=>\(\left(x+\dfrac{1}{2}\right)\cdot\dfrac{2x}{3}=0\)
=>\(x\left(x+\dfrac{1}{2}\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x+\dfrac{1}{2}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
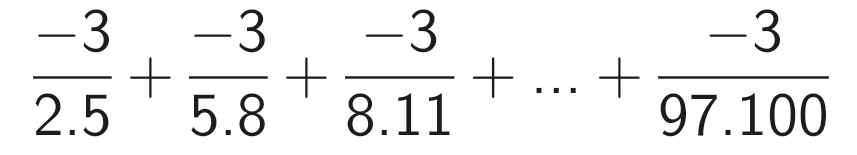
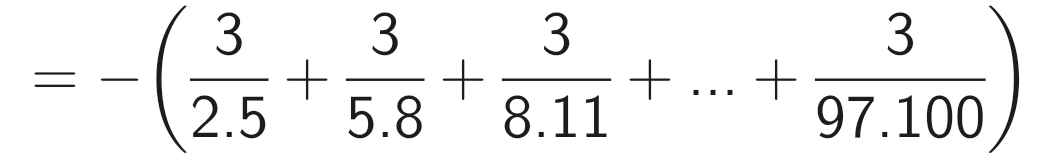
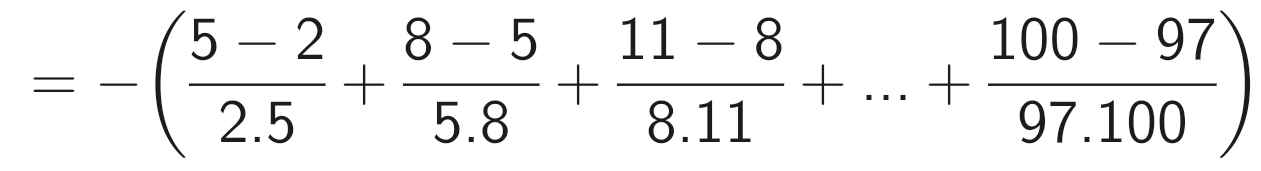
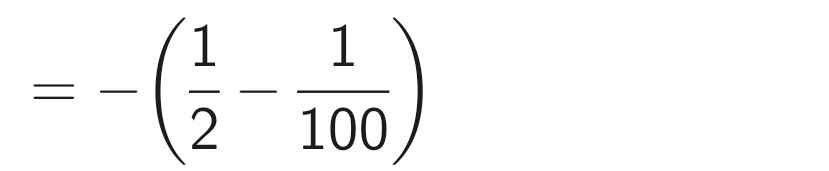
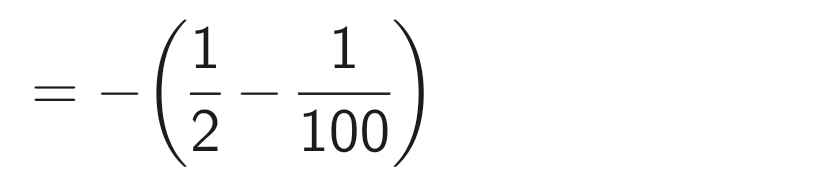

Số các số tự nhiên lẻ có 3 chữ số có thể tính như sau:
Chữ số hàng trăm có thể là một trong các số từ 1 đến 9, nên có 9 lựa chọn. Chữ số hàng chục có thể là bất kỳ số nào từ 0 đến 9, do đó có 10 lựa chọn. Chữ số hàng đơn vị phải là một số lẻ, tức là một trong các số 1, 3, 5, 7, 9, nên có 5 lựa chọn.
Vậy tổng số các số tự nhiên lẻ có 3 chữ số là:
\(9 \times 10 \times 5 = 450\)Vậy có 450 số tự nhiên lẻ có 3 chữ số.
like mình nhé