Cho A = 1/2^1 +2/2^2 +3/2^3+... +100/2^100. Hãy so sánh A vs 2. Giúp mik bài này vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Không mất tổng quát giả sử $a\geq b\geq c$
$\Rightarrow \frac{1}{a}\leq \frac{1}{b}\leq \frac{1}{c}$
$\Rightarrow \frac{4}{5}=\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\leq \frac{3}{c}$
$\Rightarrow c\leq 3,75$. Mà $c$ là stn khác 0 nên $c=1,2,3$
Nếu $c=1$ thì $\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{c}=-\frac{1}{5}<0$ (vô lý - loại)
Nếu $c=2$ thì $\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{c}=\frac{3}{10}$
Do $\frac{1}{a}\leq \frac{1}{b}$ nên $\frac{3}{10}=\frac{1}{a}+\frac{1}{b}\leq \frac{2}{b}$
$\Rightarrow b\leq 6,66$
Do $b$ là số tự nhiên và $b\geq c$ nên $b=2,3,4,5,6$
Thay vào tìm $a$ ta thấy $b=4; a=20$ và $b=5, a=10$
Nếu $c=3$ thì $\frac{1}{a}+\frac{1}{b}=\frac{4}{5}-\frac{1}{c}=\frac{7}{15}$
Do $\frac{1}{a}\leq \frac{1}{b}$ nên $\frac{7}{15}=\frac{1}{a}+\frac{1}{b}\leq \frac{2}{b}$
$\Rightarrow b\leq 4,28$
Mà $b$ là và $b\geq c=3$ nên $b=3;4$. Thay vào tìm $a$ thấy không thỏa mãn.
Vậy $(a,b,c)=(2,4,20), (2,5,10)$ và hoán vị.


c; \(\dfrac{x}{10}\) = \(\dfrac{-2}{5}\)
\(x\) = \(\dfrac{-2}{5}\) x 10
\(x\) = - 4
Vậy \(x\) = - 4

\(x-\dfrac{1}{4}=1+\dfrac{3}{4}\)
\(x-\dfrac{1}{4}=\dfrac{7}{4}\)
\(x=\dfrac{7}{4}+\dfrac{1}{4}\)
\(x=\dfrac{8}{4}\)
\(x=2\)
Vậy \(x=2\)

số học sinh gái là:
32-17=15 (hs)
học sinh gái bằng số phần trăm học sinh cả lớp là :
15 : 32 =0,46875=46,875%
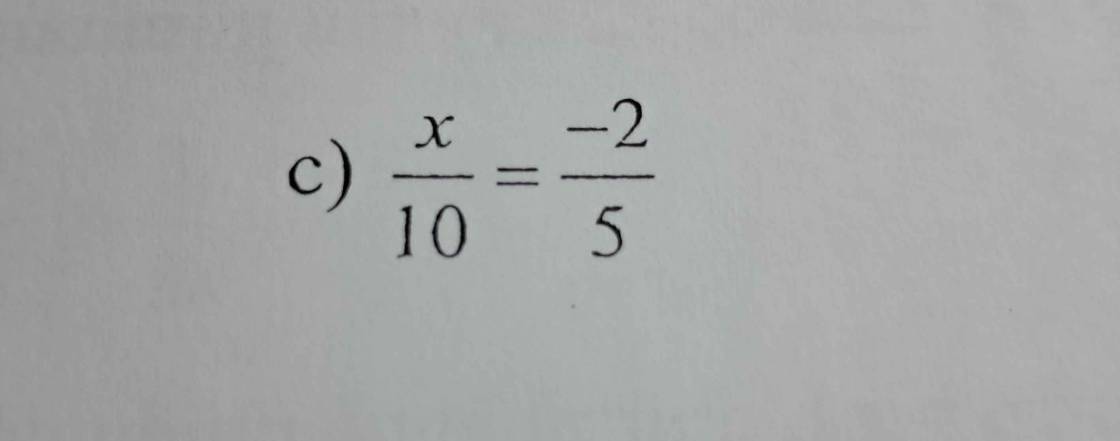
Lời giải:
$A=\frac{1}{2}+\frac{2}{2^2}+\frac{3}{2^3}+...+\frac{100}{2^{100}}$
$2A=1+\frac{2}{2}+\frac{3}{2^2}+....+\frac{100}{2^{99}}$
$\Rightarrow 2A-A=1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^{99}}-\frac{100}{2^{100}}$
$\Rightarrow A+\frac{100}{2^{100}}=1+\frac{1}{2}+\frac{1}{2^2}+....+\frac{1}{2^{99}}$
$2(A+\frac{100}{2^{100}})=2+1+\frac{1}{2}+...+\frac{1}{2^{98}}$
$\Rightarrow 2(A+\frac{100}{2^{100}})-(A+\frac{100}{2^{100}}) = 2-\frac{1}{2^{99}}$
$\Rightarrow A+\frac{100}{2^{100}}=2-\frac{1}{2^{99}}$
$\Rightarrow A=2-\frac{1}{2^{99}}-\frac{100}{2^{100}}<2$
Bạn lưu ý lần sau viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.