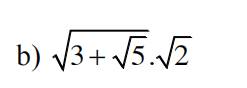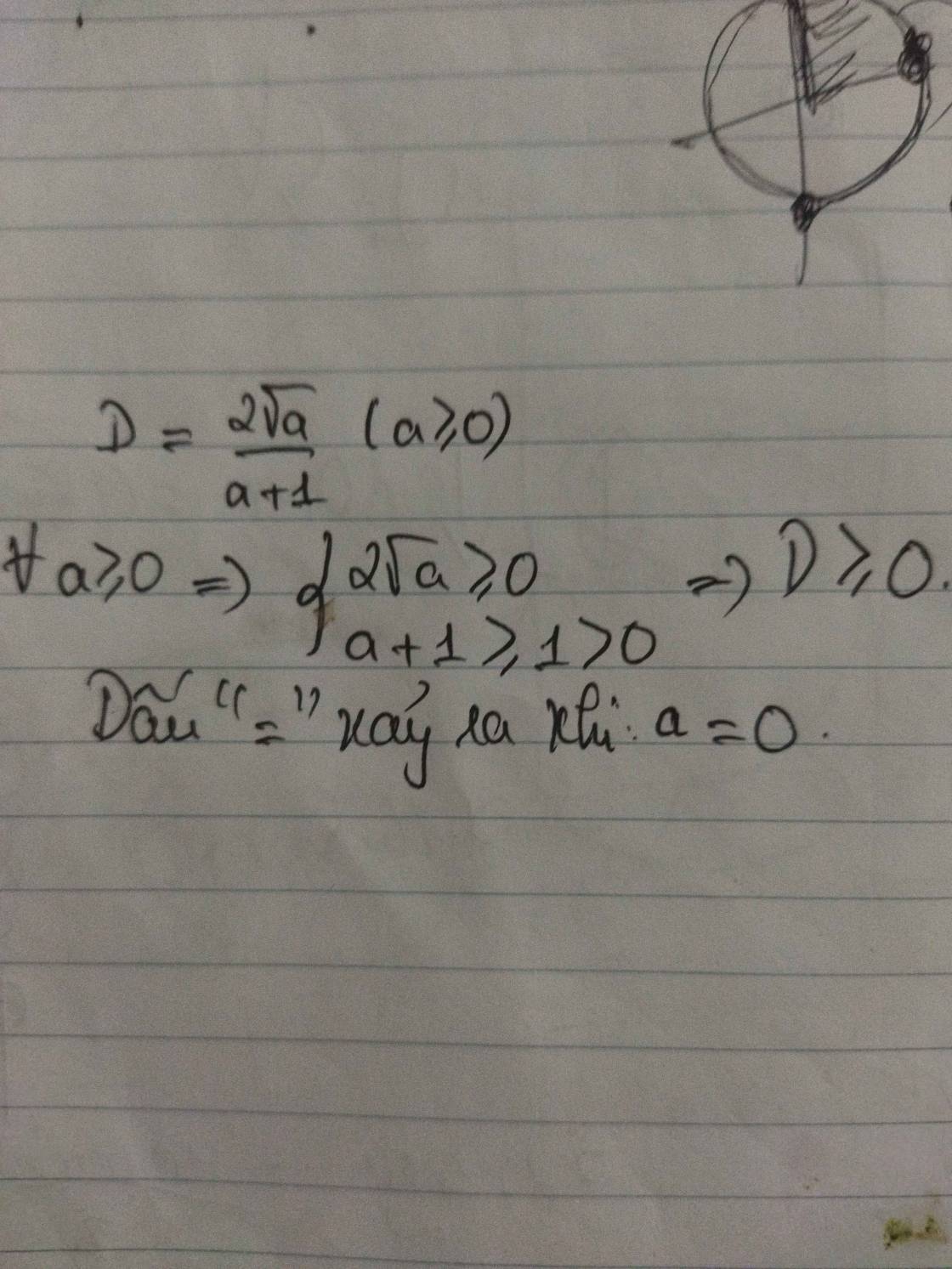Để chứng minh rằng biểu thức 34n+1 + 2.32n+2 - 21 chia hết cho 64, ta cần sử dụng phương pháp toán học gọi là "chứng minh bằng quy nạp". Bước 1: Kiểm tra điều kiện ban đầu - Khi n = 0, ta có: - Biểu thức ban đầu = 34(0) + 1 + 2.32(0) +2 -21 = -20. - Vì -20 không chia hết cho số nguyên dương nào khác của số nguyên tố lớn nhất trong các số nguyên tố nhỏ hơn hoặc bằng căn bậc hai của số này (tức là căn bậc hai của |64|), nên không thể kết luận rằng biểu thức trên chia hết cho 64. Bước 2: Giả sử giả thiết quy nạp - Giả sử với một giá trị nguyên dương k (k ≥0), biểu thức sau: P(k):=34k+1 +2.32k+2-21 Chia hết cho số nguyên tố lớn nhất trong các số nguyên tố nhỏ hơn hoặc bằng căn bậc hai của |64|. Bước 3: Chứng minh công thức quy nạp - Ta cần chứng minh rằng nếu P(k) chia hết cho 64, thì P(k+1) cũng chia hết cho 64. - Giả sử P(k) chia hết cho 64, tức là tồn tại một số nguyên dương a sao cho: P(k) = 64a. - Ta cần chứng minh rằng tồn tại một số nguyên dương b sao cho: P(k+1) = 34(k+1)+1 +2.32(k+1)+2 -21 = 34k +35 +2.32k +36 -21 = (34k+1 +2.32k+2 -21) + (34*34 + 2*32*36). Vì biểu thức trong ngoặc đơn là giá trị cố định không phụ thuộc vào k, ta có thể viết lại biểu thức trên thành: P(k+1) = (P(k)) + C, trong đó C là một giá trị cố định không phụ thuộc vào k. - Như vậy, ta có: P(k+1) = (P(K)) + C = (64a) + C. - Với a và C là các số nguyên dương, ta có thể viết lại biểu thức trên thành: P(K+1)=b * |64|, trong đó b=a+C. Bước 4: Kết luận Vì đã xác nhận rằng nếu P(k) chia hết cho 64 thì P(k+1) cũng chia hết cho 64, và với giá trị ban đầu n=0, biểu thức không chia hết cho 64, ta có thể kết luận rằng biểu thức 34n+1 +2.32n+2 -21 không chia hết cho 64 với mọi số nguyên dương n.

đúng hay sai e không biết em làm trên chat gpt

\(\dfrac{\sqrt{a}+3}{\sqrt{a}-2}-\dfrac{\sqrt{a}-1}{\sqrt{a}+2}+\dfrac{a-12}{a-4}\)(\(a>2\))

\(=\dfrac{\left(\sqrt{a}+3\right)\left(\sqrt{a}+2\right)-\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)+a-12}{a-4}\)

\(=\dfrac{a+5\sqrt{a}+6-a+3\sqrt{a}-2+a-12}{a-4}\)

\(=\dfrac{a+8\sqrt{a}-8}{a-4}\)

Bài 5

a) Số tiền chị Lan nhận được:

y = 3000000 + 5000x (đồng)

b) Để chị Lan nhận được 10000000 đồng thì số áo chị phải may là:

(1000000 - 3000000) : 5000 = 1400 (cái)

Bài 6

a) ∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

∆ABC vuông tại A, AH là đường cao

⇒ AH.BC = AB.AC

⇒ AH = AB . AC : BC

= 6 . 8 : 10

= 4,8 (cm)

b) Do M là trung điểm của AC

⇒ AM = AC : 2

= 8 : 2

= 4 (cm)

∆AMB vuông tại A

⇒ tanAMB = AB/AM

= 4/5

⇒ ∠AMB ≈ 39⁰

c) ∆AMB vuông tại A có AK là đường cao

⇒ AB² = BK.BM (1)

∆ABC vuông tại A có AH là đường cao

⇒ AB² = BH.BC (2)

Từ (1) và (2) ⇒ BK.BM = BH.BC

\(\sqrt{3+\sqrt{5}}\cdot\sqrt{2}\)

\(=\sqrt{2\cdot\left(3+\sqrt{5}\right)}\)

\(=\sqrt{6+2\sqrt{5}}\)

\(=\sqrt{\left(\sqrt{5}\right)^2+2\cdot\sqrt{5}\cdot1+1^2}\)

\(=\sqrt{\left(\sqrt{5}+1\right)^2}\)

\(=\left|\sqrt{5}+1\right|\)

\(=\sqrt{5}+1\)

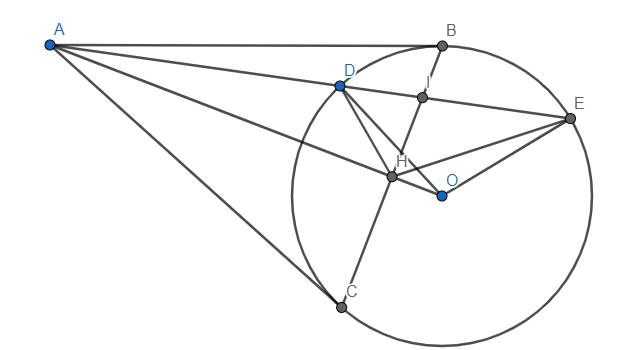
a) Do AB, AC tiếp xúc (O) tại B, C nên \(\widehat{OBA}=90^o\) và \(OA\perp BC\) tại H.

 Xét tam giác OAB vuông tại B có đường cao BH, ta có \(OB^2=OA.OH\)

 Mà \(OB=OD\left(=R_{\left(O\right)}\right)\) nên \(OD^2=OA.OH\). Từ đó suy ra \(\dfrac{OD}{OA}=\dfrac{OH}{OD}\). Từ đó dễ dàng suy ra 2 tam giác OHD và ODA đồng dạng.

b) Tam giác OAB vuông tại B có đường cao BH nên \(AB^2=AH.AO\)

 Mặt khác, ta có \(\widehat{ABD}=\widehat{AEB}\) vì chúng lần lượt là góc tạo bởi tiếp tuyến, dây cung và góc nội tiếp cùng chắn cung BD.

 \(\Rightarrow\Delta ABD~\Delta AEB\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AE}=\dfrac{AD}{AB}\Rightarrow AB^2=AD.AE\)

Từ đó suy ra \(AH.AO=AD.AE\) hay \(\dfrac{AH}{AD}=\dfrac{AE}{AO}\). Do đó \(\Delta AHE~\Delta ADO\left(c.g.c\right)\) \(\Rightarrow\widehat{AEH}=\widehat{AOD}\) hay tứ giác OHDE nội tiếp.

 \(\Rightarrow\widehat{AHD}=\widehat{DEO}=\widehat{ODE}=\widehat{OHE}\)

\(\Rightarrow90^o-\widehat{AHD}=90^o-\widehat{OHE}\) \(\Rightarrow\widehat{DHI}=\widehat{EHI}\).

Ta suy ra được đpcm.

\(\sqrt{\dfrac{11}{540}}\)

\(=\dfrac{\sqrt{11}}{\sqrt{540}}\)

\(=\dfrac{\sqrt{11}}{\sqrt{6^2\cdot15}}\)

\(=\dfrac{\sqrt{11}}{6\sqrt{15}}\)

\(=\dfrac{\sqrt{11}\cdot\sqrt{15}}{6\sqrt{15}\cdot\sqrt{15}}\)

\(=\dfrac{\sqrt{165}}{6\cdot15}\)

\(=\dfrac{\sqrt{165}}{90}\)

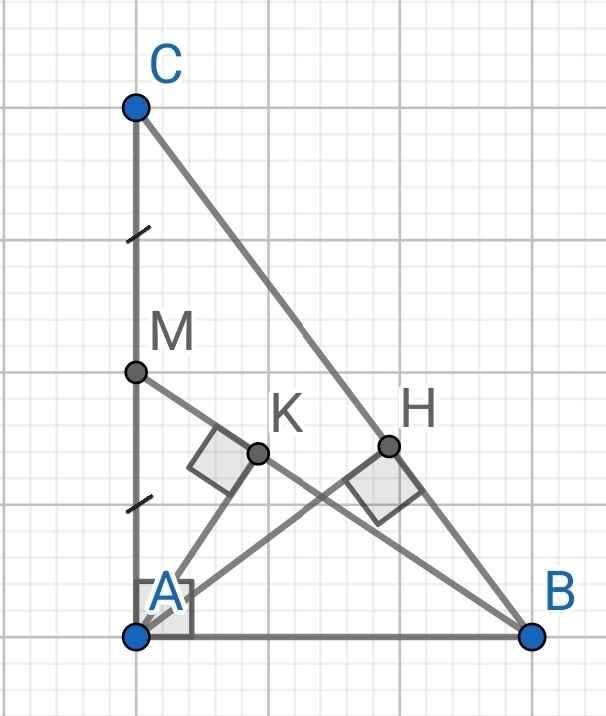
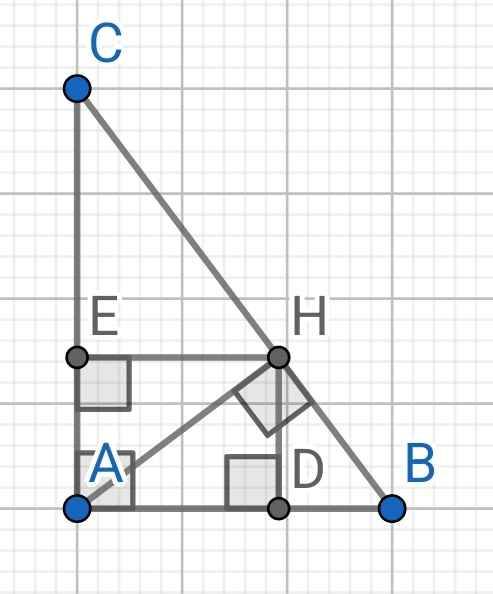1) ∆ABC vuông tại A, AH là đường cao

⇒ AH² = BH.CH = 4.9 = 36

⇒ AH = 6 (cm)

tanB = AH/BH = 6/4 = 3/2

⇒ ∠B ≈ 56⁰

2) a)

Do D, E lần lượt hình chiếu của H lên AB, AC

⇒ HD ⊥ AB và HE ⊥ AC

Tứ giác ADHE có:

∠HEA = ∠EAD = ∠ADH = 90⁰

⇒ ADHE là hình chữ nhật

giup mih voi sos:(

Min D = 0 tại a =0    

DK: a≥0
Với dk ta có \(a+1\ge2\sqrt{a}\Leftrightarrow\dfrac{2\sqrt{a}}{a+1}\le1\)
Vậy GTLN của D là 1 khi a=1(Bất đẳng thức Cô si)