10 đ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}=k\)
=>\(\left\{{}\begin{matrix}x-1=2k\\y+3=4k\\z-5=6k\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2k+1\\y=4k-3\\z=6k+5\end{matrix}\right.\)
-3x-4y+5z=50
=>-3(2k+1)-4(4k-3)+5(6k+5)=50
=>\(-6k-3-16k+12+30k+25=50\)
=>8k+34=50
=>8k=16
=>k=2
=>\(\left\{{}\begin{matrix}x=2\cdot2+1=5\\y=4\cdot2-3=8-3=5\\z=6\cdot2+5=12+5=17\end{matrix}\right.\)

Giải:
Tổng số viên bi là: 5 + 5 = 10 (viên bi)
Xác xuất của biến cố lấy được viên bi màu đỏ là:
5 : 10 = \(\frac12\)
Xác xuất của biến cố lấy được viên bi màu xanh là:
5 : 10 = \(\frac12\)
Kết luận:
a; Xác xuất của biến cố lấy được viên bi màu đỏ là: \(\frac12\)
b; Xác xuất của biến cố lấy được viên bi mà xanh là: \(\frac12\)
a: Số cách bốc 1 viên bi bất kì trong hộp là:
5+5=10(cách)
Xác suất bốc được viên bi đỏ là \(\dfrac{5}{10}=\dfrac{1}{2}\)
b: Xác suất bốc được viên bi xanh là \(\dfrac{5}{10}=\dfrac{1}{2}\)

Thể tích của bể là:
50 x 20 x 40 = 40 000 ( cm3 )
Sau khi lấy đi 3600 cm3 thì thể tích nước còn lại trong bể là:
40 000 - 3 600 = 36 400 ( cm3 )
Mực nước trong bể sau khi lấy đi 3600 cm3 là:
36 400 : ( 50 x 20 ) = 36,4 ( cm )
a) Thể tích bể:
50.20.40 = 40000 (cm³)
b) Thể tích nước còn lại trong bể:
40000 - 3600 = 36400 (cm³)
Chiều cao mực nước còn lại trong bể:
36400 : 50 : 20 = 36,4 (cm)

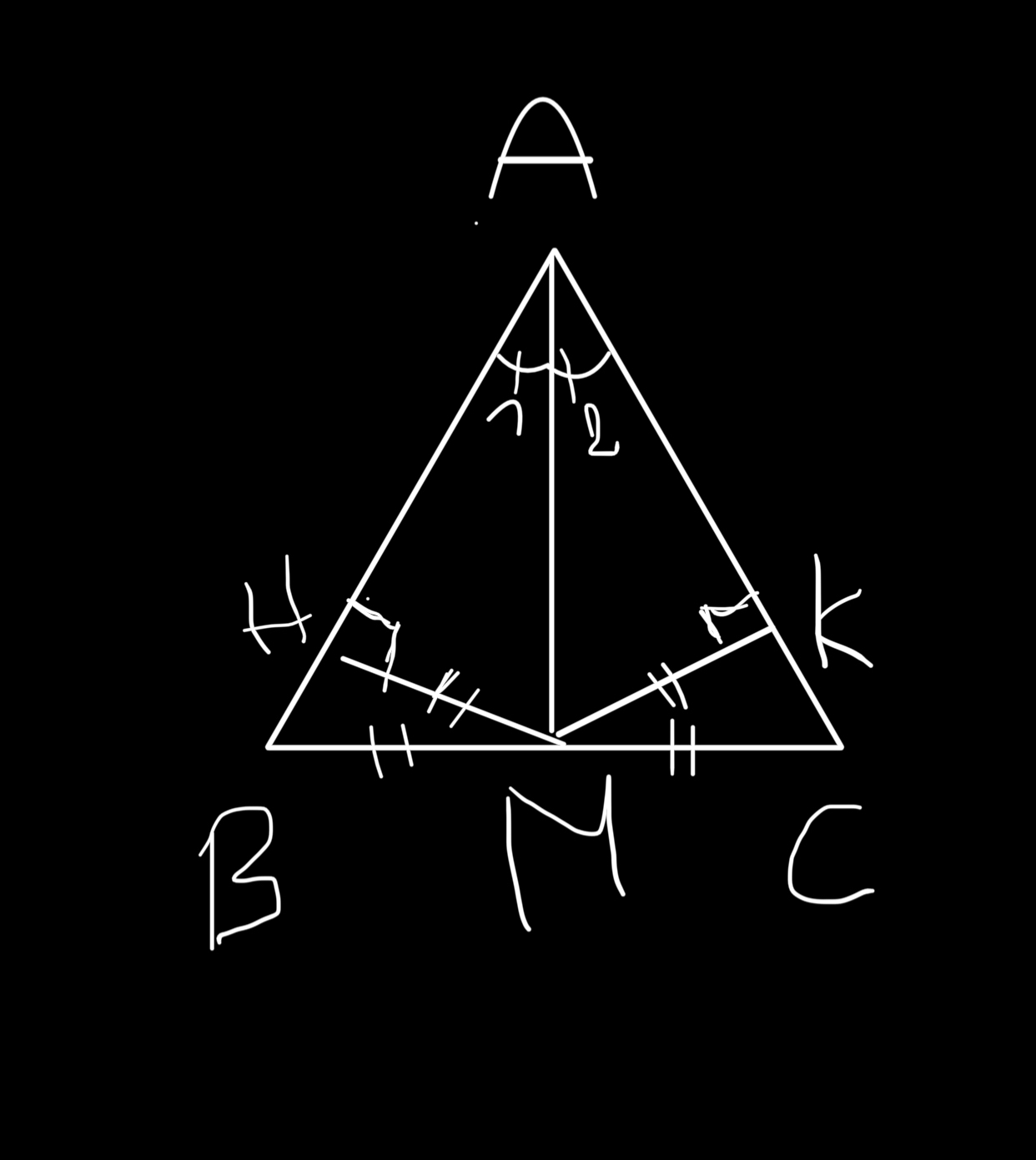
Ký hiệu vậy chưa được em. Vì em ký hiệu vậy nghĩa là BM = CM = HM = KM
Trong khi chỉ có BM = CM; HM = KM

5x/7 = 10/-3
=> 5x.(-3) = 7.10
5x.(-3) = 70
5x = 70/-3
x = -70/3 : 5
x = -14/3
Vậy x = -14/3
#ngophuongloan(chipcuti)
Chúc bạn học tốt hjhj!!
Vì \(\frac{5x}{7}=\frac{10}{-3}\) là một tỉ lệ thức
\(\Rightarrow5x.\left(-3\right)=7.10\)
\(5x.\left(-3\right)=70\)
\(5x=70:\left(-3\right)\)
\(5x=\frac{-70}{3}\)
\(x=\left(-\frac{70}{3}\right):5\)
\(x=-\frac{14}{13}\)
Vậy \(x=-\frac{14}{13}\)

Diện tích mảnh vườn hình chữ nhật là : 35 . 28 = 980 (\(m^2\))
Số ki-lô-gam cà chua thu hoạch được trên cả mảnh vườn là :
980 : 4 . 3 = 735 (kg)
Đ/s : 735 kg
giải
Diện tích mảnh vườn hình chữ nhật là:
35 . 28 =980 (m2)
Tổng số kg cà chua thu hoạch được trên mảnh vườn là:
980:4= 254 (kg)
sai cho tớ xl ạ

\(\dfrac{x}{4}=\dfrac{x\cdot2}{4\cdot2}=\dfrac{2x}{8}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{8}=\dfrac{y}{5}=\dfrac{2x-y}{8-5}=\dfrac{12}{3}=4\\ \dfrac{2x}{8}=4\Rightarrow x=16\\ \dfrac{y}{5}=4\Rightarrow y=20\)
vậy x = 16; y = 20
có x/4=y/5 suy ra 2x/8= y/5
áp dụng t/c của dãy tỉ số bằng nhau ta có
2x/8=y/5=2x-y/8-5=4
suy ra
2x/8=4 y/5=4
x=16 y=20
Olm chào em, cảm ơn đánh giá của em về chất lượng bài giảng của Olm, cảm ơn em đã đồng hành cùng Olm trên hành trình tri thức. Chúc em học tập hiệu quả và vui vẻ cùng Olm em nhé!
a good festival