Cho hình thang ABCD với hai đáy là AB và CD thòa mãn AB + CD = AD. Hai đường chéo AC và BD cắt nhau tại E , qua E kẻ đường thẳng song song AB cắt AD tại F . CMR góc BFC = 90 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ảnh minh họa:
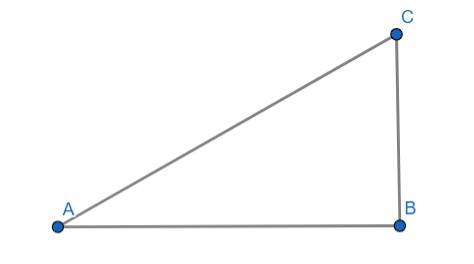
Với AC là đoạn máy bay cần bay và BC là độ mà máy bay đạt được
Ta có: \(sinA=\dfrac{BC}{AC}\Rightarrow AC=\dfrac{2000}{sin25^o}\approx4732,4\left(m\right)\)
Vậy để đạt độ cao 2000m thì máy bay cần bay khoảng 4732,4m

a) \(\sqrt{4x^2-4x+1}=5\)
\(\Leftrightarrow\sqrt{\left(2x-1\right)^2}=5\)
\(\Leftrightarrow\left|2x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=5\left(x\ge\dfrac{1}{2}\right)\\2x-1=-5\left(x< \dfrac{1}{2}\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\left(tm\right)\\x=-2\left(tm\right)\end{matrix}\right.\)
b) \(3\sqrt{x-2}-\sqrt{4x-8}+4\sqrt{\dfrac{9x-18}{4}}=14\) \(\left(x\ge2\right)\)
\(\Leftrightarrow3\sqrt{x-2}-\sqrt{4\left(x-2\right)}+4\cdot\dfrac{\sqrt{9x-18}}{2}=14\)
\(\Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+2\sqrt{9\left(x-2\right)}=14\)
\(\Leftrightarrow\sqrt{x-2}+6\sqrt{x-2}=14\)
\(\Leftrightarrow7\sqrt{x-2}=14\)
\(\Leftrightarrow\sqrt{x-2}=2\)
\(\Leftrightarrow x-2=4\)
\(\Leftrightarrow x=6\left(tm\right)\)
c) \(\sqrt[3]{4x-1}=3\)
\(\Leftrightarrow4x-1=3^3\)
\(\Leftrightarrow4x-1=27\)
\(\Leftrightarrow4x=27+1\)
\(\Leftrightarrow4x=28\)
\(\Leftrightarrow x=7\)
\(a.\sqrt{4x^2-4x+1}=5\\ \Leftrightarrow\sqrt{\left(2x-1\right)^2}=5\left(ĐK:\left(2x-1\right)^2\ge0\forall x\right)\\ \Leftrightarrow\left|2x-1\right|=5\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=5+1\\2x=-5+1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\\ Vậy.S=\left\{3;-2\right\}\\ b.3\sqrt{x-2}-\sqrt{4x-8}+4\sqrt{\dfrac{9x-18}{4}}=14\\ \Leftrightarrow3\sqrt{x-2}-\sqrt{4\left(x-2\right)}+\dfrac{4\sqrt{9\left(x-2\right)}}{\sqrt{4}}=14\\ \Leftrightarrow3\sqrt{x-2}-2\sqrt{x-2}+6\sqrt{x-2}=14\\ \Leftrightarrow7\sqrt{x-2}=14\left(ĐK:x\ge2\right)\\ \Leftrightarrow\sqrt{x-2}=2\\ \Leftrightarrow x-2=4\\ \Leftrightarrow x=4+2\\ \Leftrightarrow x=6\left(tm\right)\\ Vậy,S=\left\{6\right\}\)
\(c.\sqrt[3]{4x-1}=3\\ \Leftrightarrow4x-1=27\\ \Leftrightarrow4x=27+1\\ \Leftrightarrow4x=28\\ \Leftrightarrow x=7\)

chúc học tốt :))))

Ta có:
\(a^3+b^3=2\)
\(\Rightarrow\left(a+b\right)\left(a^2-ab+b^2\right)=2\)
\(\Rightarrow a+b=\dfrac{2}{a^2-ab+b^2}\)
Mà: \(2\left(a-b\right)^2\ge0\forall a,b\)
\(\Rightarrow2\left(a^2-2ab+b^2\right)\ge0\)
\(\Rightarrow2a^2-4ab+2b^2\ge0\)
\(\Rightarrow2a^2+2a^2-4ab+2b^2+2b^2\ge2a^2+2b^2\)
\(\Rightarrow4a^2-4ab+4b^2\ge2\left(a+b\right)^2\)
\(\Rightarrow4\left(a^2-ab+b^2\right)\ge2\left(a+b\right)^2\ge\left(a+b\right)^2\)
\(\Rightarrow a^2-ab+b^2\ge\dfrac{\left(a+b\right)^2}{4}\)
\(\Rightarrow\dfrac{2}{a^2-ab+b^2}\le\dfrac{8}{\left(a+b\right)^2}\)
\(\Rightarrow a+b\le\dfrac{8}{\left(a+b\right)^2}\)
\(\Rightarrow\left(a+b\right)^3\le8\)
\(\Rightarrow a+b\le2\)
Vậy: \(A_{max}=2\)

Đặt \(f\left(x\right)=ax^3+bx^2+cx+d\left(a\inℤ^+\right)\)
\(f\left(5\right)=125a+25b+5c+d\)
\(f\left(3\right)=27a+9b+3c+d\)
\(\Rightarrow f\left(5\right)-f\left(3\right)=98a+16b+2c\)
Mà \(f\left(5\right)-f\left(3\right)=2022\) nên \(98a+16b+2c=2022\)
\(\Leftrightarrow49a+8b+c=1011\)
Lại có \(f\left(7\right)=343a+49b+7c+d\)
\(f\left(1\right)=a+b+c+d\)
\(\Rightarrow f\left(7\right)-f\left(1\right)=342a+48b+6c\) \(=6\left(57a+8b+c\right)\) \(=6\left(8a+1011\right)\) (vì \(49a+8b+c=1011\))
Mà do \(a\inℤ^+\) nên \(f\left(7\right)-f\left(1\right)\) là hợp số (đpcm)

\(VT\ge\dfrac{4}{x^2+y^2+2xy}=\dfrac{4}{\left(x+y\right)^2}\ge4\) (vì \(x+y\le1\) )
Dấu "=" xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)
Ta có đpcm

\(A=\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}+\dfrac{1}{4xy}+4xy+\dfrac{5}{4xy}\)
\(\ge\dfrac{4}{x^2+y^2+2xy}+2\sqrt{\dfrac{1}{4xy}.4xy}+\dfrac{5}{4.\dfrac{\left(x+y\right)^2}{4}}\)
\(\ge\dfrac{4}{1^2}+2+\dfrac{5}{1^2}\) (do \(x+y\le1\))
\(=11\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\dfrac{1}{2}\)
Vậy GTNN của A là 11.

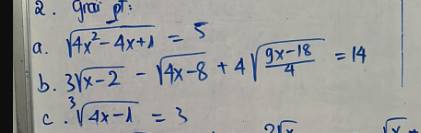
Dựng hình bình hành ABPC. Khi đó \(AD=AB+CD=CP+CD=DP\)
Ta có \(\dfrac{AB}{FE}=\dfrac{DA}{DF}\), \(\dfrac{CD}{FE}=\dfrac{DA}{AF}\)
\(\Rightarrow\dfrac{AB+CD}{FE}=DA\left(\dfrac{1}{DF}+\dfrac{1}{AF}\right)\)
\(\Rightarrow\dfrac{1}{FE}=\dfrac{DA}{DF.AF}\) \(\Rightarrow\dfrac{DF}{FE}=\dfrac{DP}{FA}\) \(\Rightarrow\dfrac{DF}{DC}=\dfrac{DP}{DA}=1\)
Từ đó \(\Delta DFC\) cân tại D. \(\Rightarrow\widehat{DFC}=\widehat{DCF}=\widehat{CFE}\) \(\Rightarrow\) FC là tia phân giác của \(\widehat{DFE}\). CMTT, FB là tia phân giác của \(\widehat{AFE}\). Do đó \(\widehat{BFC}=90^o\) (đpcm)